連立方程式で交点を求める理由を解説!これでスッキリわかります

中学2年生で一次関数を習ってからというもの、常識のように言われていることがあります。

交点を求めるには連立方程式を使います
連立方程式を用いて交点を求める問いは、中学だけでなく高校でも登場します。
つまり、どんな図形の式でも交点を求める時には連立方程式を用いるのです。
この記事では交点を求める時には連立方程式を用いる理由を解説します。
その理由を理解するにはまず『そもそも図形の式とは何でできているのか』を知る必要があるので、そこから丁寧に解説します。
この記事を読めば、今までモヤモヤしていた『交点を求める時には連立方程式を用いる理由』がスッキリわかりますよ!
【前提知識】図形の式は『方程式の解』で出来ている
【図形の式とは】
以下のような式のことを『図形の式』とします。
○比例・一次関数といった『直線』
○二次関数・三次関数といった『曲線』
○円・楕円といった『図形』
まずは、座標平面上にある図形は、その図形を表す方程式の解で出来ていることを理解しましょう。
逆に、座標平面上にある図形が通る座標は、その図形の方程式の解なのです。
例
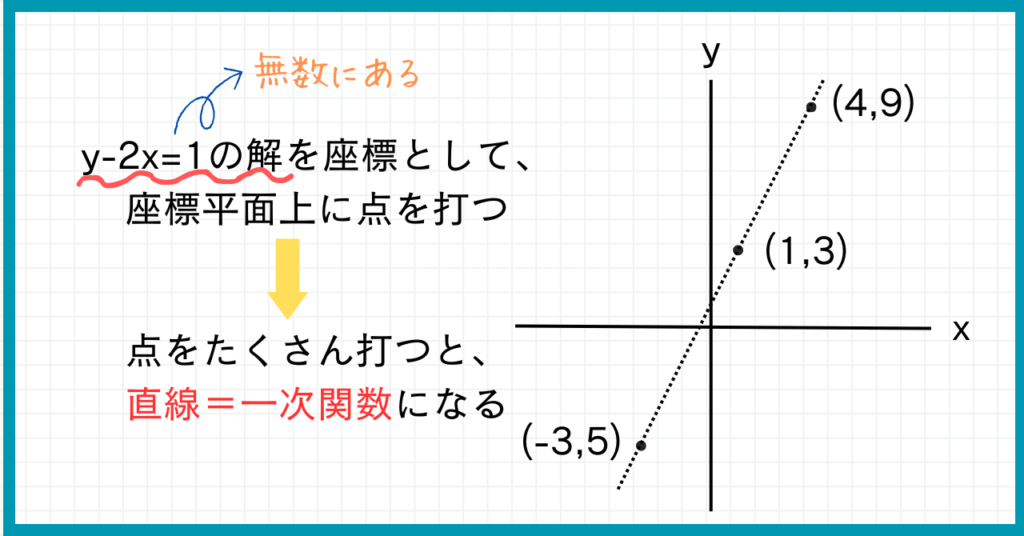
二元一次方程式$y-2x=1$の解となる点を、座標平面上に打ってみましょう。
例えば二元一次方程式$y-2x=1$の解は何でしょうか。

$x=4,y=9$
$x=1,y=3$
$x=-3,y=-5$
などなど、無数にあるね!
では、解となる点を座標平面上に打ってみましょう。
点をつなげると、直線になりそうですよね。
実際、二元一次方程式$y-2x=1$の解をもっともっとたくさん求めて座標平面上に点を打つと、直線になります。
さて、この直線に見覚えがありますよね。

一次関数だ!
二元一次方程式$y-2x=1$こそが、一次関数なのです。
$y-2x=1$を変形すると$y=2x+1$となり、一次関数の式になりますね。
もちろん、二次関数$y=3x^2$や円$x^2+y^2=9$なども同じです。
$y=3x^2$の解を座標平面上に打つと曲線(二次関数)に、$x^2+y^2=9$の解なら円になるのです。
交点とは『2つ以上の図形の式に共通する解』のこと
ここまでで、図形の方程式の解を座標として、座標平面上に点を打つとその方程式が表す図形になるとお話してきました。
逆に、座標平面上にある図形が通る座標は、その図形を表す方程式の解であることも話しましたね。
以上を踏まえて、一次関数の交点を求めるにはどうしたらいいかを考えましょう。
例
一次関数$y=2x+3$と一次関数$y=-x+6$の交点Aの座標は?
一次関数$y=2x+3$と一次関数$y=-x+6$の交点とは、その2つの一次関数が交わる点のことですよね。
では、交点ができるとはどういうことか。
ここでもう一度確認しましょう。座標平面上にある図形が通る座標は、その図形を表す方程式の解でしたよね。
つまり2つの一次関数の交点ができるということは、2つの一次関数の式に共通する解があるということです。
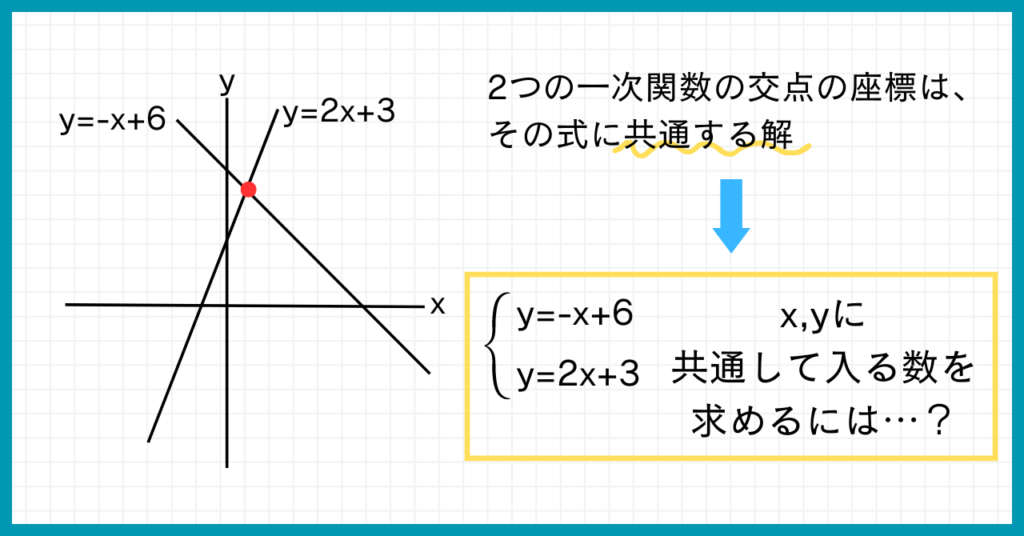
一次関数の式といえば、$x,y$の2つの文字でできた式ですよね。
では、x,yに共通して当てはまる数を求めるにはどうしたらよいでしょうか?

連立方程式だ!
交点を求めること=2つの式に共通する解を求めることなので、連立方程式を用いて交点を求めるのです。
もちろん、一次関数の交点だけでなく、様々な図形の交点を求める時も連立方程式を使います。
まとめ
連立方程式で交点を求める理由についてまとめます。
交点といえば連立方程式! と、なんとなく暗記している人が多いかと思います。
しかし、このように連立方程式を用いる理由を掘り下げてみるのも楽しいでしょう。

コメントを残す