【一次関数】yの増加量の求め方を変化の割合と増加量の関係からわかりやすく解説

中学生のあなたにとって、一次関数の中でも特にわかりにくいのは『変化の割合』と『x,yの増加量』でしょう。
ゆえに、突然『yの増加量は?』と聞かれたら戸惑ってしまいますよね。
しかし増加量を求める問題は、変化の割合と増加量の関係がわかっていれば簡単に解けるようになるのです。
この記事ではyの増加量の求め方を解説します。
yの増加量を求める前提知識として変化の割合と増加量の関係から解説するので、この記事を読めばyの増加量の求め方がすんなり頭に入りますよ!
【前提知識】x,yの増加量と変化の割合とは
まずは前提知識として、x,yの増加量と変化の割合とは何かを解説します。
x,yの増加量
まずはx,yの増加量とは何かを解説します。
例として以下の2点の『xの増加量』『yの増加量』を求めます。
例
座標A(2,3)、座標B(4,6)間の、『xの増加量』と『yの増加量』を求めましょう。
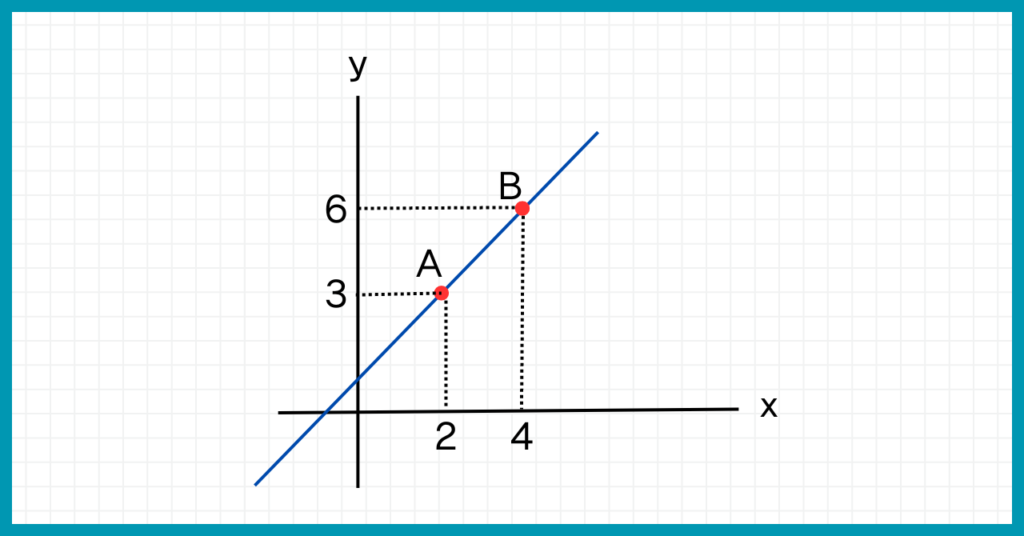
座標AB間の『xの増加量』と『yの増加量』、つまり座標AB間でどれだけx,y座標が変化したかを求めます。
座標AB間で、x座標とy座標はどれだけ変化したでしょうか?

座標Aから座標Bに行くまでに、
x座標は2から4
y座標は3から6
に変化したね
つまりxの増加量は$4-2$で$\color{red}{2}$。またyの増加量は6-3で$\color{red}{3}$です。
言い換えると、座標Aから座標Bに行くまでx座標は2だけ変化し、y座標は3だけ変化したということです。
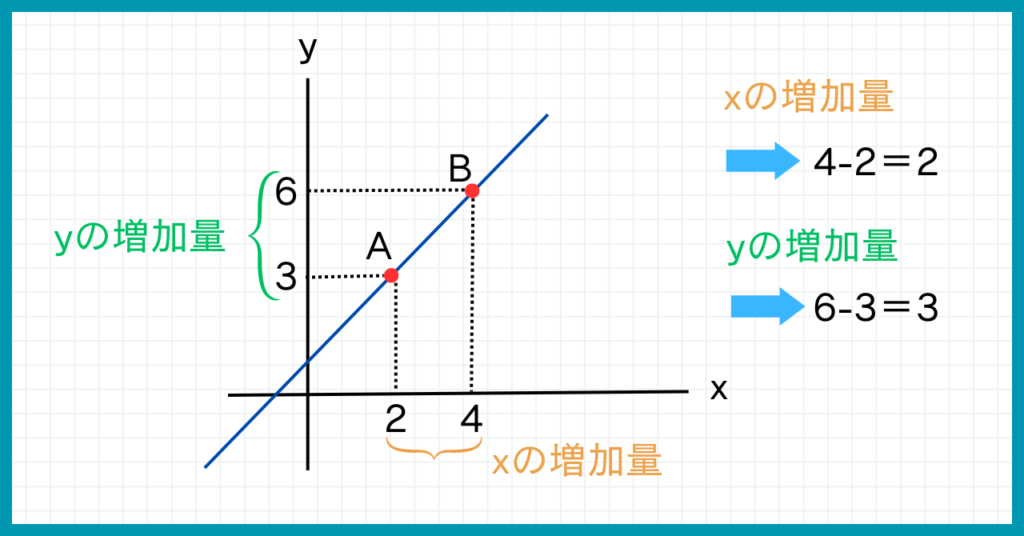
『xの増加量』『yの増加量』とは言いますが、あくまでもx座標やy座標がどれだけ変化したかを表しているので、増加だけでなく減少することもあります。
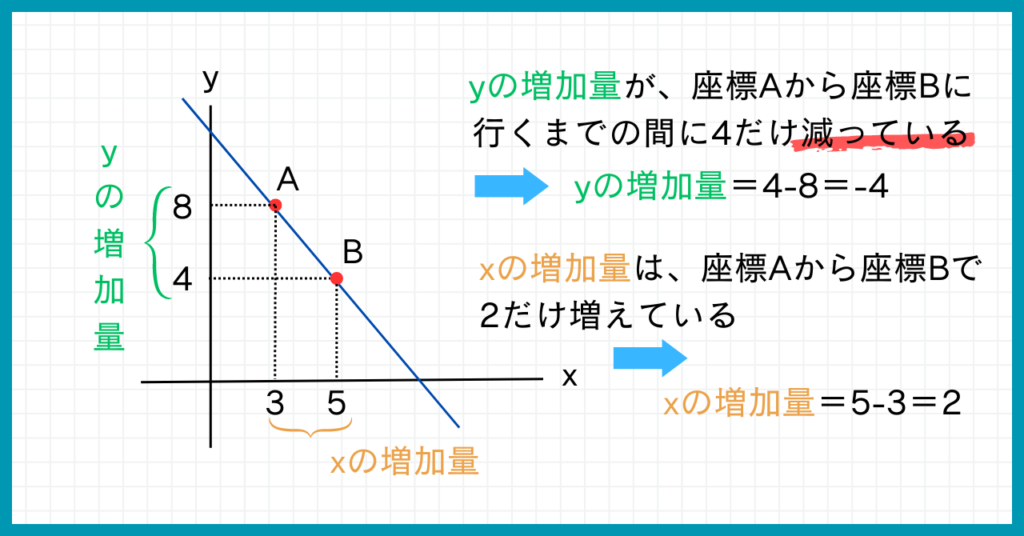
座標Aから座標Bに行く間で、xの座標の数字は増えています。
しかしy座標はどうでしょうか?

Aのy座標は8、Bのy座標は4だから、
座標Aから座標Bに行く間でy座標の数字は減っているね。
つまり座標AB間のyの増加量は$4-8=-4$と、増加量と言いながら減少しています。
このように、増加量を求めるからといって正の数しか現れないということはないので覚えておきましょう。
変化の割合とその公式
次に変化の割合とは何かを解説します。
つまり変化の割合を求めるには、まずはある座標2点間のxの増加量とyの増加量を知る必要があります。
その後、yの増加量をxの増加量で割れば、xの増加量1あたりのyの増加量つまり変化の割合を求められます。
以上のことから、変化の割合の公式が成り立ちます。
【例題】yの増加量の求め方
yの増加量を求める問いについて、以下の2パターンを解説します。
- 座標から求める
- 変化の割合の公式から求める
詳しくは以下です。
①座標から求める
例題
一次関数$y=-3x+2$のグラフ上にある座標A(1,-1)と座標B(3,-7)におけるyの増加量を求めましょう。
yの増加量とは、ある座標2点間でy座標が変化した量のことでした。
つまりyの増加量を求めるには、座標Aと座標Bの間でどれくらいy座標が変化したかを考えれば良いのです。

座標Aから座標Bに行くまでに、
y座標は-1から-7
に変化したね
よって座標Aから座標Bまでのyの増加量は$-7-(-1)=-6$です。
この場合のyの増加量を言い換えると、座標Aから座標Bまででy座標が-6だけ変化したということです。
②変化の割合の公式から求める
例題
一次関数$y=-3x+2$におけるxの増加量が6のとき、yの増加量を求めましょう。
今度はxの増加量が分かっているパターンです。
この場合は変化の割合の公式を用いて、方程式を解くようにしてyの増加量を求めます。

変化の割合がいくつかわからないよ?
一次関数$y=ax+b$の$a$にあたる数が変化の割合でしたね。

そっか!
じゃあ変化の割合は-3だ!
変化の割合は-3、xの増加量は6。
yの増加量をyとすると、変化の割合の公式を用いて以下のような式ができます。
$(変化の割合)=\displaystyle \frac{yの増加量}{xの増加量}$
$-3=\displaystyle \frac{y}{6}$
$y=-18$
よって答えは-18です。
まとめ
一次関数におけるyの増加量の求め方についてまとめます。
変化の割合や増加量については、抽象的な内容なのでわかりにくいかと思います。
しかし変化の割合や増加量の意味を押さえておけば、すんなり理解できるはずです。
公式の暗記に頼らず、言葉の意味を理解するようにしましょう。

コメントを残す