【これで理解】一次関数のグラフ2種類の描き方と共通する重要ポイントを解説

中学生のあなたは、一次関数のグラフの描き方を2種類習います。
一次関数のグラフの描き方には、①傾きと切片を用いる方法と②x切片とy切片を用いる方法がありましたね。

一次関数のグラフの描き方がわからない

グラフの描き方は2種類あるけど、両方暗記しなきゃいけないの?
この記事では一次関数のグラフの描き方2種類に共通する重要ポイントを解説した後、それぞれのグラフの描き方を解説します。
一次関数のグラフを描くポイントを知っていれば、グラフの描き方2種類を丸暗記する必要はありません。
この記事を読めば、ポイントを押さえて一次関数のグラフを描けるようになります。
【重要ポイント】どちらも『座標平面上に2点を取るため』の方法
一次関数のグラフはどんな形でしょうか?

そんなの簡単!
一次関数のグラフは直線だよ!
では、決まった直線を描くにはどうしたらいいでしょうか?
そう。直線の通る2つの点を求めて、それらの点を結べばよいのです。
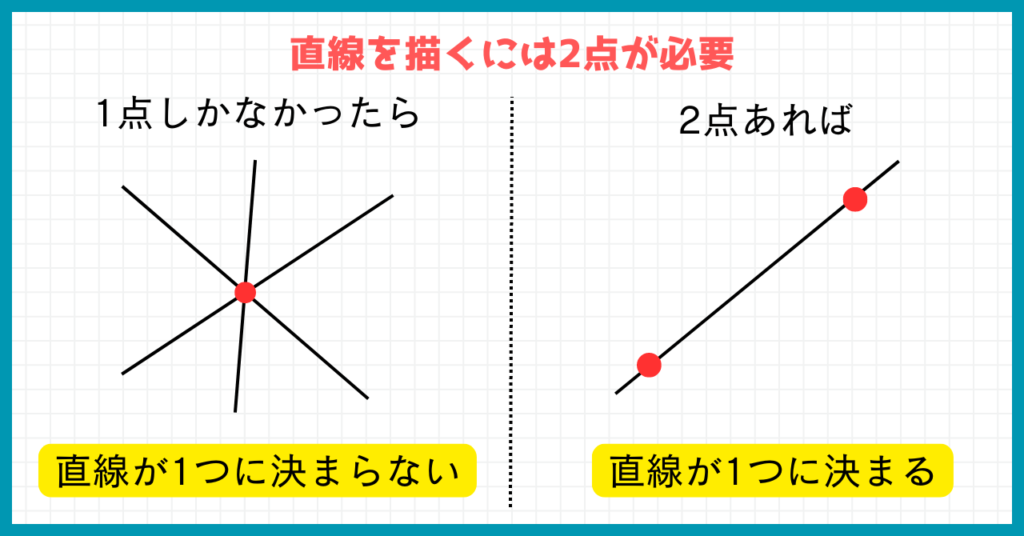
一次関数のグラフの描き方2種類『①傾きと切片を用いる方法と②x切片とy切片を用いる方法』はどちらも、方法こそ違えど直線の通る2つの点を求める手段なのです。
一次関数のグラフの描き方2種類
ここからは、一次関数のグラフの2種類の描き方を解説します。
この2種類の描き方はやり方こそ違いますが、目的は一緒です。
その目的とは座標平面上に2点をとることでしたね。
それぞれのグラフの描き方を勉強するときは、『こうして2点をとっているんだな』と理解していきましょう。
①傾きと切片を用いる方法
まずは一次関数の傾きと切片を用いて座標平面上に2点とり、グラフを描く方法を解説します。
グラフを描く手順は以下です。
『②傾きを用いて、切片の点から初めてもう一点取る』やり方を含め、例題を用いて解説します。
例題
次の一次関数のグラフを描きましょう。
- $y=2x-1$
- $y=-\frac{1}{3}x+2$
①について。
まずは手順①y軸上に切片の点を取りましょう。
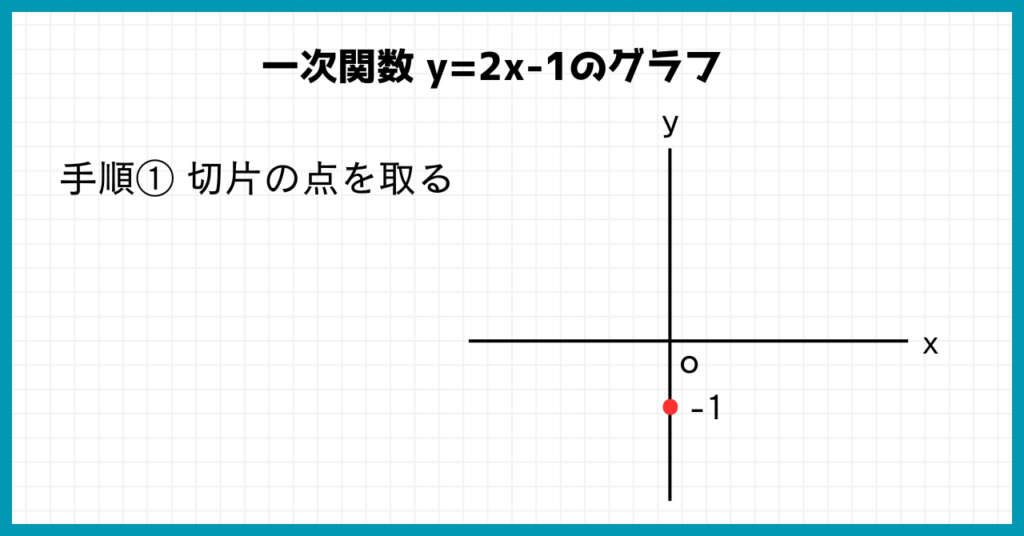
次に手順②傾きを用いて、切片の点から初めてもう一点取ります。

傾きを用いてもう一点とるって、どうやるの?
傾きを用いてもう一点取るために、まずは傾きの数を分数とみます。
その後、傾きの数の分母の数だけ右に、分子の数だけ上または下に移動し、点を打ちます。
$y=2x-1$の傾きは?

『2』です!
では、2を分数とみましょう。
$\color{red}{2=\frac{2}{1}}$とみるのです。
傾き$\frac{2}{1}$は分母が1、分子が2なので、切片から初めて右に1、上に2移動して点を打ちます。
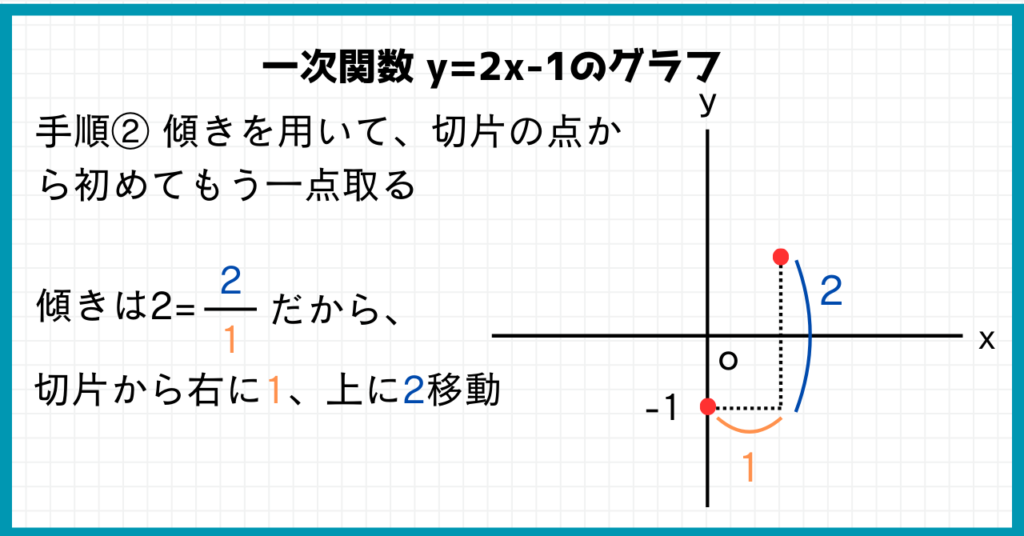
2点とれたら、あとは点を結んで終わりです。
②について。
まずは手順①y軸上に切片の点を取りましょう。
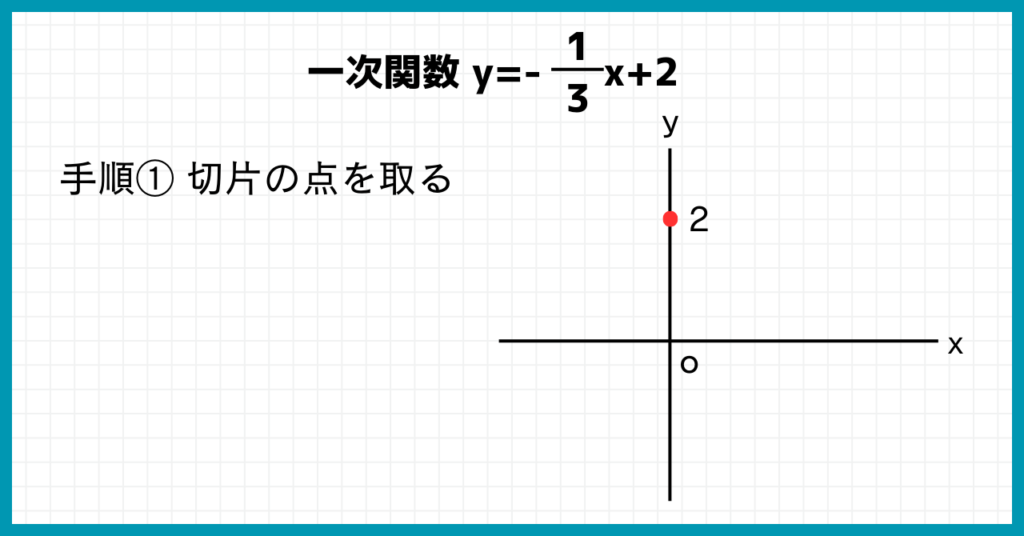
次に手順②傾きを用いて、切片の点から初めてもう一点取ります。
$y=-\frac{1}{3}+2$の傾き『-$\frac{1}{3}$』は分数なので、例題①のように整数を分数とみる作業は要りません。

傾きがマイナスの時って、どうすればいいの?
マイナスの符号を分子につけましょう。
傾き『-$\frac{1}{3}$』ではなく、傾き『$\frac{-1}{3}$』と考えるイメージです。
傾き『$\frac{-1}{3}$』は分母が3、分子が-1なので、切片から初めて右に3、下に1移動して点を打ちます。

分子がマイナスのときは、下に移動するんだったね!
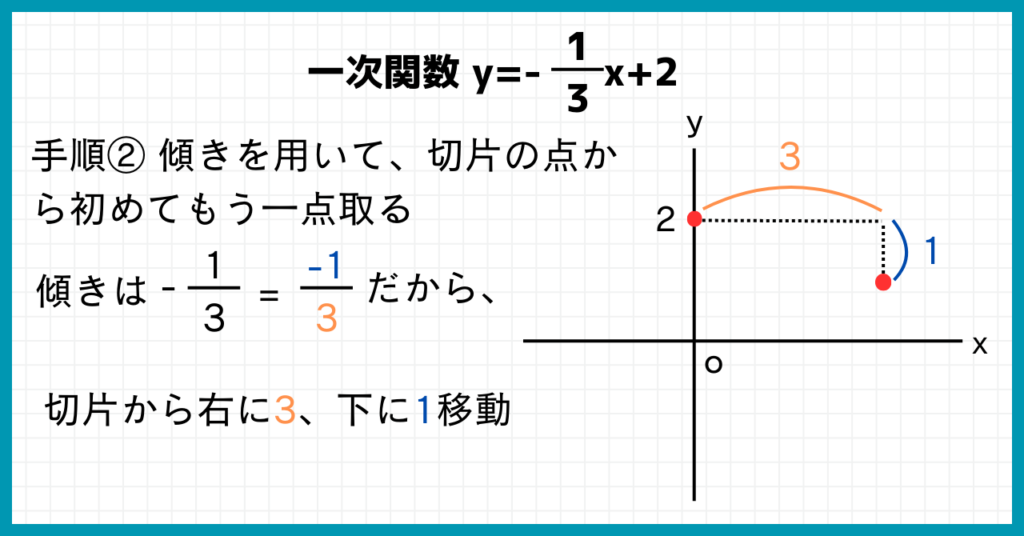
2点とれたら、あとは点を結んで終わりです。
②x切片とy切片を用いる方法
x切片とy切片を用いてグラフを描く手順は以下です。
x切片はx軸上にあるので、x切片を求めるためには一次関数の式にy=0を代入します。
ということは、y切片を求めるためにはどうしたらいいでしょうか?

y切片はy軸上にあるから、y切片を求めるには一次関数の式にx=0を代入すればいいね!
こうしてx切片とy切片を求めれば座標平面上に2点取れるので、一次関数のグラフを描けます。
では、例題を解いてみましょう。
例題
次の一次関数のグラフを描きましょう。
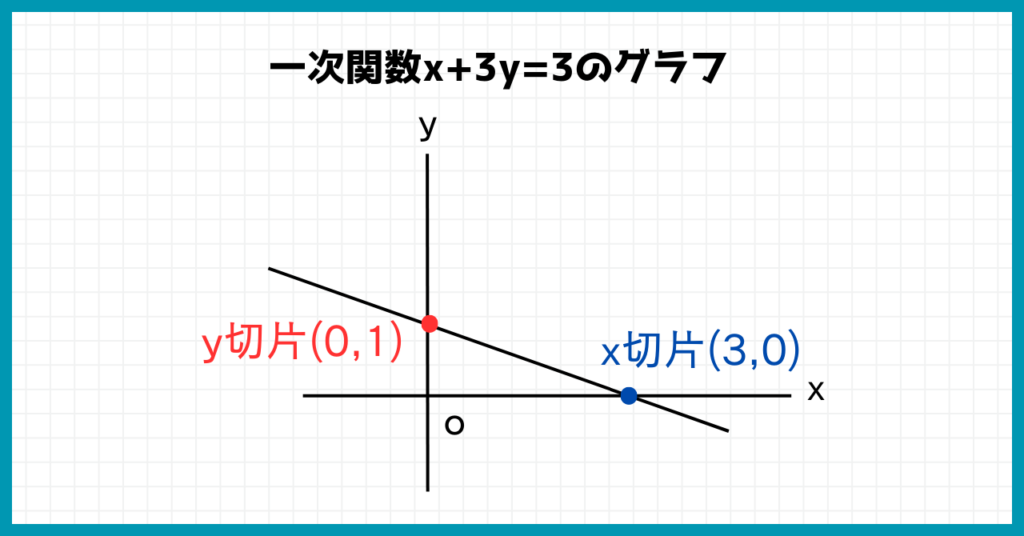
$x+3y=3$
x切片の座標とy切片の座標を求めましょう。
まずはx切片を求めていきます。

x切片を求めるには、式にy=0を代入すれば良いんだったね
$x+3y=3$
$x+3×0=3$
$x=3$
よってx切片の座標は(3,0)です。
次にy切片を求めます。
y切片を求めるためには、式にx=0を代入するんでしたね。
$0+3y=3$
$3y=3$
$y=1$
よってy切片の座標は(0,1)です。
こうしてx切片の座標とy切片の座標の2点を求められました。
あとは座標平面上にその2点をとり、線で結ぶだけです。
まとめ
一次関数のグラフは直線です。
直線を描くには、その直線が通る2つの点を求め、それらを結べば良いのでしたね。
この記事で紹介した2種類の描き方は、どちらも直線を描くために2点を求める方法です。
2種類のグラフの描き方を丸暗記するのではなく、どちらのやり方でも本質は変わらないのだと理解してくださいね。

コメントを残す