【aじゃない】二次関数『変化の割合』の求め方を解説！裏技も紹介

一次関数の変化の割合はaの値を言えばよかったのに、二次関数は違うの！？

　そう思っているあなたのために書きました。

　この記事ではまず変化の割合とはそもそもなんなのか？ を解説したあと、二次関数の変化の割合の求め方を解説します。

　さらに中学校の教科書に載っている求め方だけでなく、裏技も紹介します。

　また、一次関数の変化の割合は『a』だったのに、二次関数ではそうはいかない理由も解説します。

変化の割合とは何か

　そもそも変化の割合とは何か、あなたは説明できますか？

　つまり変化の割合を求めるためには、yの増加量をxの増加量で割れば良いのです。

　yの増加量やxの増加量がピンとこない人は、以下の記事も参考にしてくださいね。

二次関数『変化の割合』求め方と問題演習

　まずは二次関数『変化の割合』の求め方を2種類紹介します。

　最初は教科書に載っている基本の求め方をマスターしましょう。

　その後で、二次関数の変化の割合を簡単に求められる裏技を紹介します。

【基本】変化の割合の求め方

　二次関数の変化の割合を求めるためには、変化の割合を求める公式を用います。

　さて、変化の割合を求める公式を覚えていますか？

一次関数を習ったときに出てきたよね

　例題をやってみましょう。

　$(変化の割合)=\frac{(yの増加量)}{(xの増加量)}$

　この公式を使うためには、まずyの増加量とxの増加量を求めましょう。

　$y=3x^2$より、$x=1$のとき$y=3$で、$x=3$のとき$y=27$

　よって変化の割合は、

　$\frac{(27-3)}{(3-1)}$

　=12

変化の割合を求める裏技

　公式$(変化の割合)=\frac{(yの増加量)}{(xの増加量)}$を使う方法では、変化の割合を求めるためにxとyの増加量を求める必要がありました。

ちょっとめんどくさいなぁ……

　そんなあなたのために、二次関数の変化の割合を求める裏技を教えます。

　裏技を使って、基本の求め方と同じ例題の変化の割合を求めてみましょう。

　x座標が、$x=1$から$x=3$まで変化します。

　また、a=3なので、裏技の公式に当てはめると以下のようになります。

　変化の割合は、

　3(3+1)

　=12

めっちゃ簡単じゃん！

　新たに公式を覚える必要がありますが、簡単に二次関数の変化の割合を求められるのでオススメです。

　ただし、注意点があります！

　例えば一次関数の変化の割合は求められないので気をつけてくださいね。

【問題演習】変化の割合の求め方

　ここからは変化の割合を求める問題をやってみましょう。

　①について。

　変化の割合を求めるためには、xの増加量とyの増加量が必要でしたね。

　$y=5x^2$より、$x=1$のとき$y=5$で、$x=3$のとき$y=45$

　$(変化の割合)=\frac{(yの増加量)}{(xの増加量)}$なので、

　変化の割合は、

　$\frac{(45-5)}{(3-1)}$

　=20

　裏技公式(変化の割合)=a(p+q)を使うと、

　a=5で、xが1から3まで変化するから

　5(1+3)=20

　②について。

　$y=5x^2$より、$x=-3$のとき$y=45$で、$x=0$のとき$y=0$

　$(変化の割合)=\frac{(yの増加量)}{(xの増加量)}$なので、

　変化の割合は、

　$\frac{0-45}{0-(-3)}$

　=-15

　裏技公式(変化の割合)=a(p+q)を使うと、

　a=5で、xが-3から0まで変化するから

　5{0+(-3)}=-15

二次関数『変化の割合』がaじゃない理由

　ここまで話してきた通り、二次関数の変化の割合を単に『$y=ax^2$のaの値』とはできません。

　これは一次関数とは異なりますね。

一次関数の時は、変化の割合は$y=ax+b$のaでよかったのに、

二次関数の時はなんで$y=ax^2$のaの値とはできないの？

　ここからは　二次関数の変化の割合がaじゃない理由を解説します。

【答え】二次関数は変化の割合が一定じゃないから

　そもそも変化の割合とは、xの増加量1あたりのyの増加量のことでしたね。

　一次関数は変化の割合、つまりxの増加量1あたりのyの増加量が一定で、それが$y=ax+b$のaにあたります。

　しかし二次関数は、xの増加量1あたりのyの増加量が一定ではないため、二次関数の変化の割合を単にaとは言えないのです。

　この後で一次関数と二次関数それぞれについて、変化の割合の違いを詳しく解説します。

【図解】一次関数と二次関数『変化の割合』の違い

　変化の割合とは、ある関数でのxの増加量1あたりのyの増加量のことでした。

　一次関数の変化の割合と二次関数の変化の割合をグラフで表すと、以下のようになります。

　まずは一次関数です。

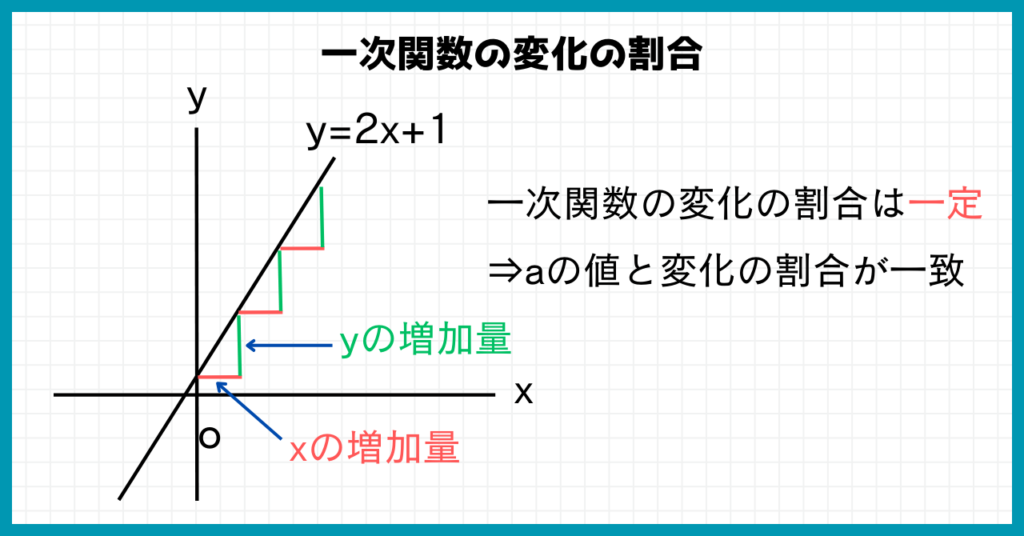
　一次関数のグラフのどこをとっても、変化の割合は一定ですね。

　次は二次関数を見ていきましょう。

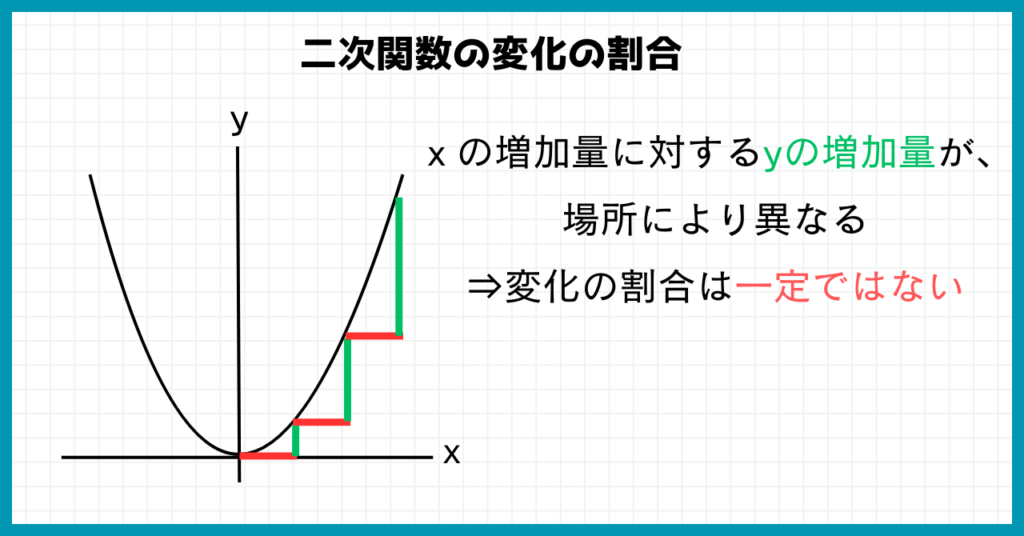
　二次関数はグラフの場所によって、変化の割合が異なります。

xの増加量が同じでも、場所によってyの増加量が違ってるね！

　このように、一次関数は変化の割合は一定なのに対し、二次関数はxの増加量をどこからどこまでとったかによりyの増加量が変わってしまうため、変化の割合が一定ではありません。

　よって二次関数の変化の割合を求める時は、いちいち公式を用いて計算しなければならないのです。

まとめ

　二次関数の変化の割合を答える時、aにあたる値を答えてしまったことがある人もいることでしょう。

　しかし変化の割合の意味さえわかっていれば、それは違うとわかりますよね。

　二次関数の式を見ただけでは変化の割合はわかりませんが、変化の割合を求める裏技もあるので、テストで聞かれた時は絶対に正解しましょうね！