【小学生でもわかる】n角形の内角の和『公式』をもう忘れないための解説

一見単純に見えても忘れてしまい安いのがn角形の内角の和『公式』です。
なんども覚え直しては忘れ、今日もまた検索してしまったという人が多いことでしょう。
この記事ではn角形の内角の和『公式』を紹介したあと、公式を忘れないように公式の成り立ちを解説します。
もう検索しなくていいように、この記事を読んでしっかり覚えていきませんか?
【公式】n角形の内角の和
まずは公式を見てみましょう。
180に『°』がついていたり、謎にn-2が出てきたり……。
なにげに忘れやすいんですよね。
もう公式を忘れたくないあなたは、この先もぜひ読んでくださいね!
【図解】これでもう忘れない!n角形の内角の和『公式』の意味
n角形の内角の和『公式』は、単純に見えて覚えにくいし忘れやすいです。
そういうときこそ、公式の成り立ちを理解しましょう!

公式の成り立ちって、難しそう
n角形の内角の和『公式』は、実は小学生でもわかる知識で説明できます。
さらに図を用いてわかりやすく解説しているので、難しそうだと考えてるあなたも安心してくださいね。
n角形の中に三角形がいくつあるかを考える
n角形の内角を求めるにはどうしたらいいか。
そう。n角形の中に、いくつ三角形があるのかを考えればよいのです!
さて、三角形の内角の和はいくつでしょうか?

そんなの簡単!
180°だよね!
n角形の中に三角形がいくつあるかがわかれば、三角形の数だけ180をかければn角形の内角の和がわかるのです。
例えば、四角形の内角の和は知っていますか?

四角形の内角の和は
360°!
四角形の中には、三角形が2つあります。
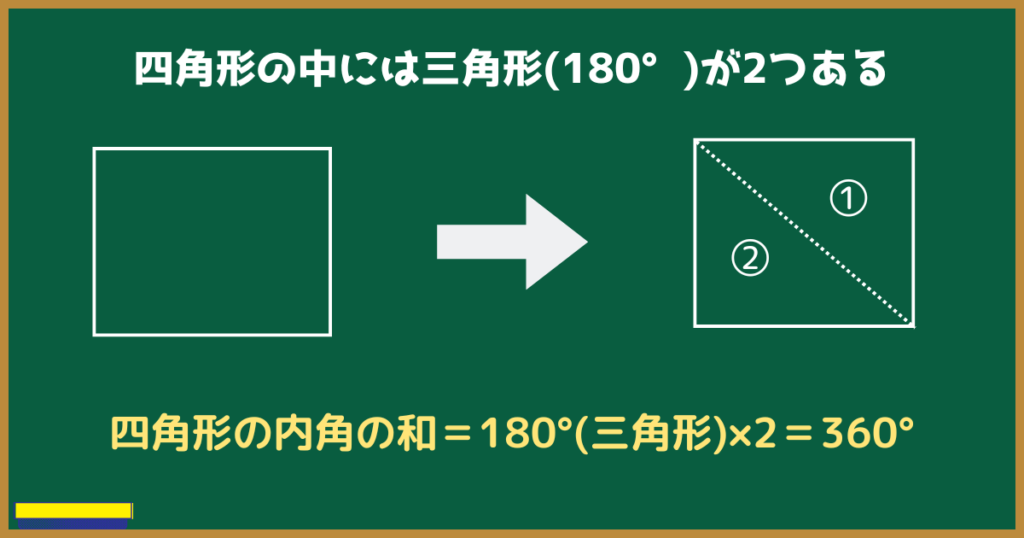
四角形の中には三角形が2つあるので、四角形の中には180°が2つ。
つまり四角形の内角の和は180°×2=360° というわけなのです。
$n-2$はn角形の中にある三角形の数
四角形の中には三角形が2つあるので、四角形の内角の和は180°×2=360° でした。
つまり公式『$180°×(n-2)$』の$n-2$はn角形の中にある三角形の数を表しているのです。
$n-2$とはつまり、n角形のnの数より2小さい数だけ、その中に三角形があるということです。
例えば四角形ならその中に2つ三角形がありますよね。

じゃあ、
五角形なら3つ
六角形なら4つの三角形があるってこと?
その通りです!
では、実際に図を見てみましょう。
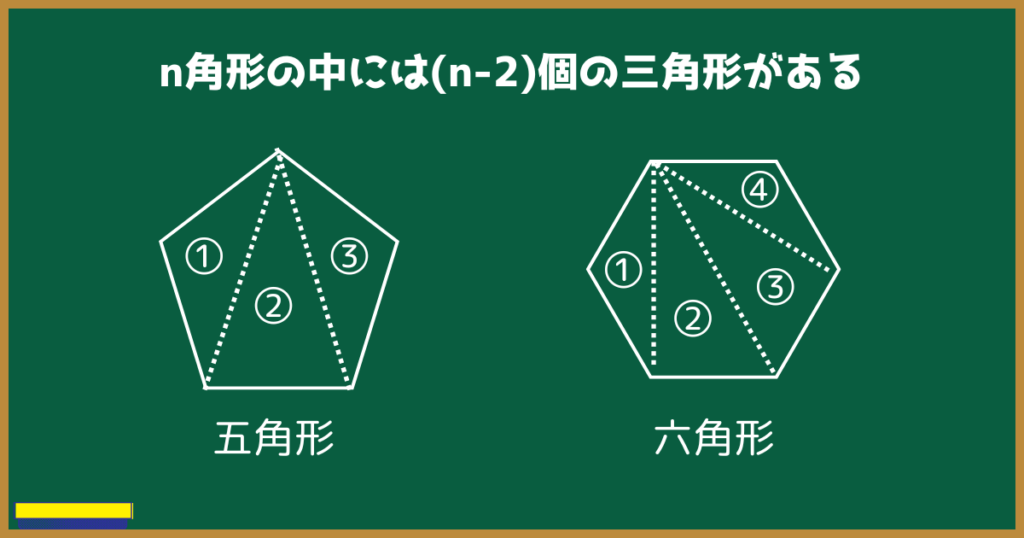
このように、n角形の中には三角形が(n-2)個あります。
n角形の内角の和を求めるには、n角形の中にある三角形の数だけ180をかければよいのです。
よって、公式が$180°×(n-2)$となるのでした。
まとめ
n角形の内角の和は、中学校で突然出てきたものではありません。
小学生でもわかる理屈を、nという記号を用いて公式にしたにすぎません。
かえって覚えづらくなってしまいましたが、この記事を読んで公式の成り立ちを理解すれば難しいことはありませんよね。

コメントを残す