【塾講師が解説】半球の表面積の求め方！断面を忘れずに

　半球の表面積を求める問いで間違えて、｢あれ？｣と思った人は多いのではないでしょうか。

　そんなあなたは、半球の断面を計算に加えているかどうかを確認してみましょう。

　塾講師の私の経験から、半球の断面を計算に加え忘れる人はとても多いのです。

　この記事では、半球の表面積の求め方を解説します。

　ポイントを意識して解けるように解説しているので、学校で習っても解き方がよくわからなかった人はぜひ読んでくださいね。

【前提知識】球の表面積を求める公式

　まずは球の表面積を求める公式を確認しましょう。

　忘れていた人は、必ず覚えてくださいね。

【例題】半球の表面積の求め方

　ここからは半球の表面積の求め方を、例題を用いて解説します。

　よくわる間違いも紹介しているので、自分が該当していないか確認してみてくださいね。

【ポイント】球の断面を忘れない

　ここからは例題を用いて、半球の表面積の求め方を解説します。

例題

次の半球の表面積を求めなさい。

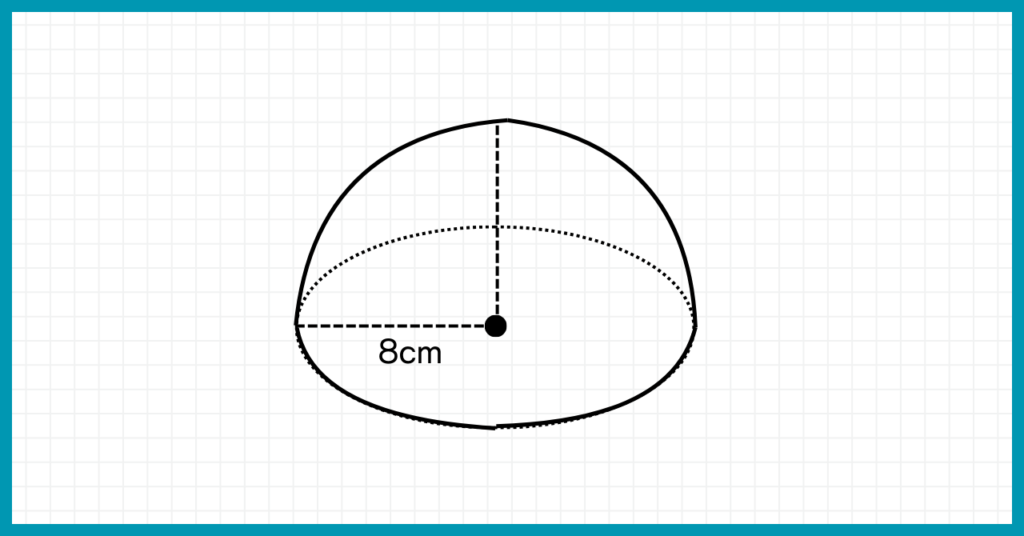
　まずは半球の表面積を求めるポイントを教えますね。

　例題の半球の半径は8cmですね。

　これは丸々一個の球だと考えると、その表面積は$4πr^2$より$4π×8^2$です。

　半球なので、$4π×8^2$の$\frac{1}{2}$ですね。

　さらに、半球には断面があるので、半球の断面の面積も加えましょう。

　半球の断面は半径8cmの円なので、$8^2×π&ですね。

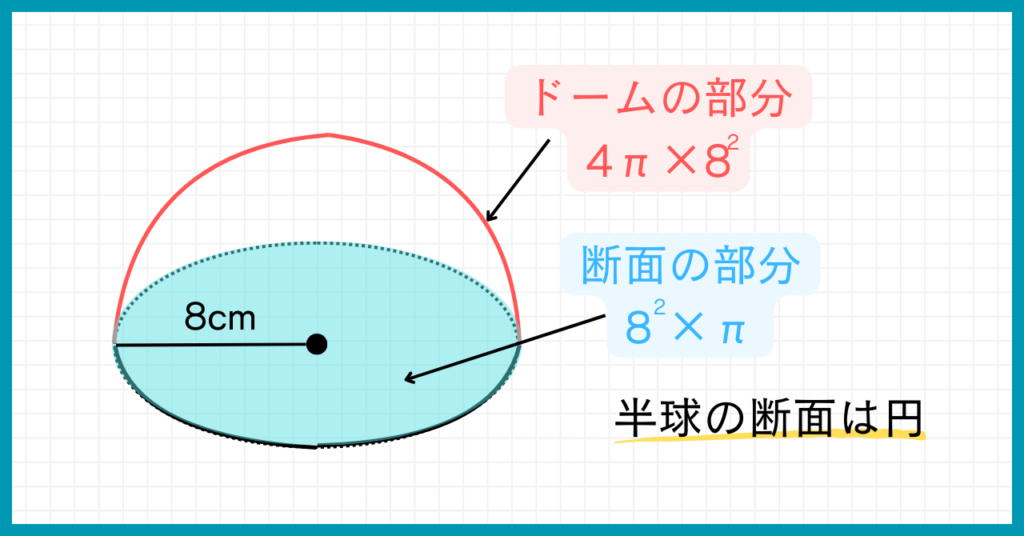
　以下で解答をまとめます。

よくある間違い

半球の表面積だから、$4πr^2$をした後に$\frac{1}{2}$すればいいんだ！

例題の式は｢$4π×8^2×\frac{1}{2}=128$｣で、

答えは｢128cm^2｣だ！

　塾講師の経験から、このように早とちりしてしまう中学生はとても多いです。

　半球の体積なら単に$\frac{1}{2}$をすれば良いのですが、表面積はそうはいきません。

　$4π×8^2×\frac{1}{2}$だけだと半球のドームの部分だけなので、断面が入っていませんね。

　必ず、断面の円の面積を計算に加えましょう。

まとめ

　塾講師の経験から、半球の表面積を求めるときに断面を計算するのを忘れる人が多いです。

　この記事を読んだあなたは、忘れないでくださいね。