【知らなきゃ損】半球の表面積を一発で求める裏技公式

　半球の表面積を求める時は、半球のドームの部分と断面の部分をそれぞれ求めなければいけません。

　それって面倒だな、と思ったことはありませんか？

　実は、半球の表面積を一発で求める公式があるのです。

　この記事では、半球の表面積を一発で求める公式を紹介します。

　その公式が成り立つ理由も解説しているので、ぜひ最後まで読んでくださいね。

半球の表面積を求める裏技公式

　まずは半球の表面積を求める裏技公式をを紹介します。

　半球の表面積を$S=3×πr^2$と見ると、断面の円の面積は$πr^2$なので、半球の表面積は断面の面積の3倍だということですね。

裏技公式が成り立つことを確認

　半球の表面積は$S=3πr^2$、つまり断面の円の面積の3倍です。

　このことを、次の例題を用いて確認します。

　ここでは裏技公式ではなく、(球の表面積×1/2)+(断面の面積)をする方法で解きましょう。

　裏技公式を知らなければ、この方法で解くことになりますよね。

　ピンとこない人は、以下の記事を参考にしてください。

例題

次の半球の表面積を求めなさい。

ただし、半径はrとする。

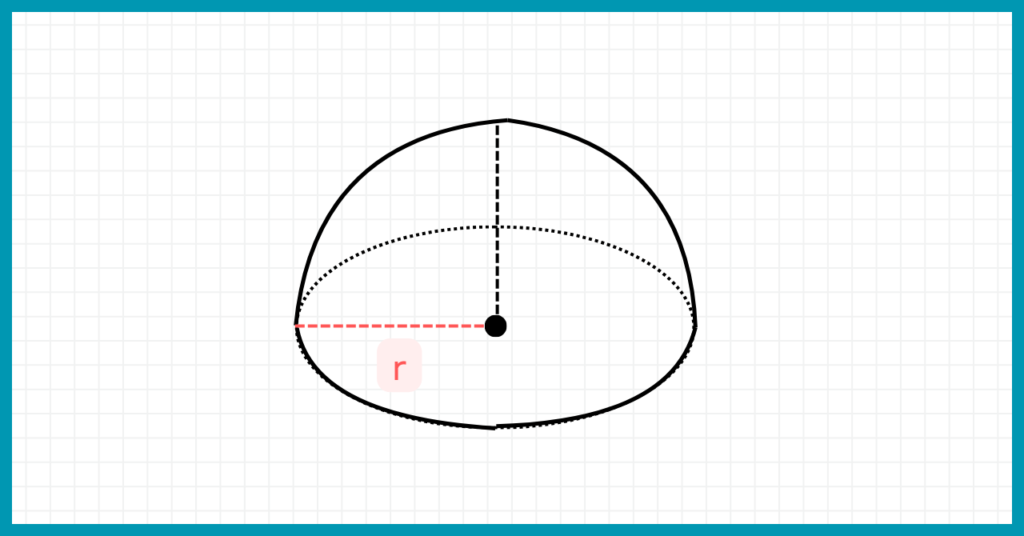
　球の表面積を求める公式を覚えていますか？

球の表面積を求める公式は$4πr^2$だね！

　これは半球なので、$4πr^2$にさらに$\frac{1}{2}$するわけです。

　また、半球の断面を計算に加えるのを忘れてはいけません。

　半球の断面は円なので、球の半径を用いて断面の円の面積を用います。

　例題の半球の半径はrなので、表面積を求める式は以下のようになります。

　$πr^2$は断面の円の面積ですよね。

　半球の表面積を求めたら最終的に$3πr^2$となったので、半球の表面積は断面の円の面積の3倍になると言えます。

まとめ

　半球の表面積を求める公式を知らなければ、半球のドームの部分と半球の断面の部分の面積をそれぞれ求めなければいけないので面倒ですよね。

　しかしこの公式を知っていれば楽に解けます。

　それほど大変な暗記ではないので、ぜひ覚えておいてくださいね。