【数学ⅠA】集合で出てくる用語・記号と公式の意味をまとめてわかりやすく解説

数学ⅠAの単元『集合』は、高校で初めて習う内容なので難しいですよね。
集合を難しくしているのは、次々と出てくる新しい用語や記号。
さらにド・モルガンの法則などの公式を駆使して解く問題もあるので、集合に苦手意識をもっても無理はありません。
この記事では、最初に集合に出てくる用語・記号、公式を一覧でまとめています。
そのあとで、集合に出てくる用語と公式について詳しく解説します。
必要に応じて図も用意しているので、この記事を読めば集合の基礎知識が整理できます!
集合に出てくる用語・記号と公式の一覧
集合について学習する上で、押さえておきたい用語と記号をまとめます。
さらに以下の公式も覚えましょう。
以下ではそれぞれの用語・記号と公式について、詳しく解説します。
気になるところがあれば、リンクから飛んでくださいね。
集合に出てくる用語・記号の意味を解説
ここからは集合に出てくる用語について、意味を解説します。
さらに用語に対応する記号も紹介します。
①集合『$A=\{1,2,3\}$』『$A=\{x|1≦x≦3\}$』
数学における集合とは、数や文字の集まりのことです。
集合一つ一つには『A』や『B』などと名前が付けられます。
例えば、集合Aについて1,2,3,4,5が含まれるとしたら、以下の2つの表し方をします。
集合の表し方
集合Aに1,2,3,4,5が含まれるときの表し方
- $A=\{1,2,3,4,5\}$
- $A=\{x|1≦x≦5\}$
集合の表し方は、①のように書き並べる方法と、②のように範囲を表す方法があります。

$A={x|1≦x≦5}$ってどういう意味?
まずは集合Aに含まれる数を、全て$x$とします。
そのあとで$x$の範囲を$1≦x≦5$指定し、集合Aには1,2,3,4,5が含まれると言っているのです。
②要素『$1 \in A$,$1 \notin A$』
集合を構成している一つ一つの数や文字を、要素と呼びます。
例えば$A=\{1,2,3,4,5\}$の要素は、1と2と3と4と5です。
要素であることを記号$1 \in A$で表し、要素でないことを$1 \notin A$で表します。
要素の表し方
$A=\{1,2,3,4,5\}$について
- 1はAの要素なので、$1 \in A$と表す。
- 7はAの要素ではないので、$7 \notin A$と表す。
③集合の個数『$n(A)=3$』
集合の要素の個数を表すには、$\color{red}{n(A)=○○}$と書きます。
例えば$A=\{1,2,3,4,5,6\}$であれば、要素は6個なので$n(A)=6$と書きます。
④空集合『$\varnothing$』
数学における集合には、要素が一つもない集合が存在します。
要素が一つもない集合を空集合といい、記号$\varnothing$で表します。
例えば集合Aが空集合のとき、$A={\varnothing}$と書きます。
⑤部分集合『$A \subset B$,$A \not \subset B$』
ある集合の要素が別の集合の要素全てを含むとき、別の集合はある集合の部分集合であるといいます。
以下の集合Aと集合Bを見てください。
部分集合の例
$A=\{1,2,3\}$
$B=\{1,2,3,4,5\}$
$C=\{10,11\}$
Aの要素が全てBに含まれる。
これを$A \subset B$または$B \supset A$と表す。
Cの要素はBの要素に含まれていないので、$C \not \subset B$または$B \not \supset C$と表す。
部分集合について理解を深めるため、以下の例題をやってみましょう。
例題
$A=\{1,2,3,4\}$の部分集合を全て答えよ。

集合Aの部分集合だから、Aの要素だけをもつ集合を書けばいいんだね

Aの部分集合は、{1}{2}{3}{4}
他には{1,2}{1,3}{1,4}とか……
まずは解答をまとめます。
解答
$A=\{1,2,3,4\}$の部分集合は、
{1},{2},{3},{4},
{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},
{1,2,3},{1,2,4},{1,3,4},{2,3,4},
{1,2,3,4},∅
部分集合には元の集合とまったく同じ要素を持つ集合と、空集合があります。
例題でいう{1,2,3,4}のような、元の集合とまったく同じ要素を持つ集合を真部分集合と言います。
⑥共通部分『$A \cap B$』
2つ以上の集合があるとき、共通の要素を共通部分といい、 記号$\cap$(キャップ)で表します。
$A \cap B$の読み方は、『AキャップB』もしくは『AかつB』です。
共通部分の例
$A=\{1,2,3,4,5\}$
$B=\{2,4,6,8,10\}$
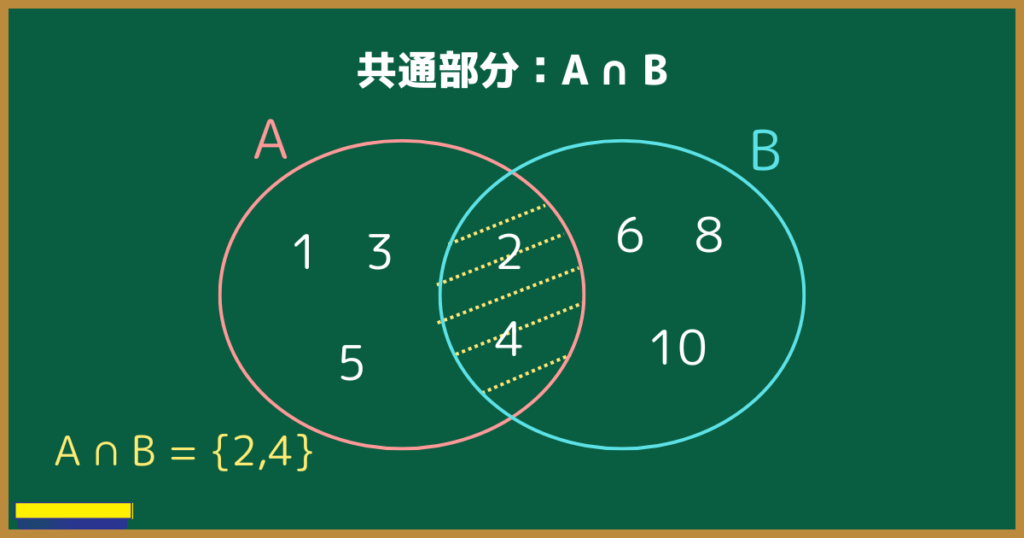
2,4が共通なので、$A \cap B=\{2,4\}$
共通部分は、図でもイメージできるようにしましょう。
⑦和集合『$A \cup B$』
2つ以上の集合があるとき、それらの要素を全て集めた集合を和集合と言います。
和集合は記号$\cup$と表し、読み方は$A \cup Bであれば『AカップB』もしくは『AまたはB』です。
和集合の例
$A=\{1,2,3,4,5\}$
$B=\{2,4,6,8,10\}$
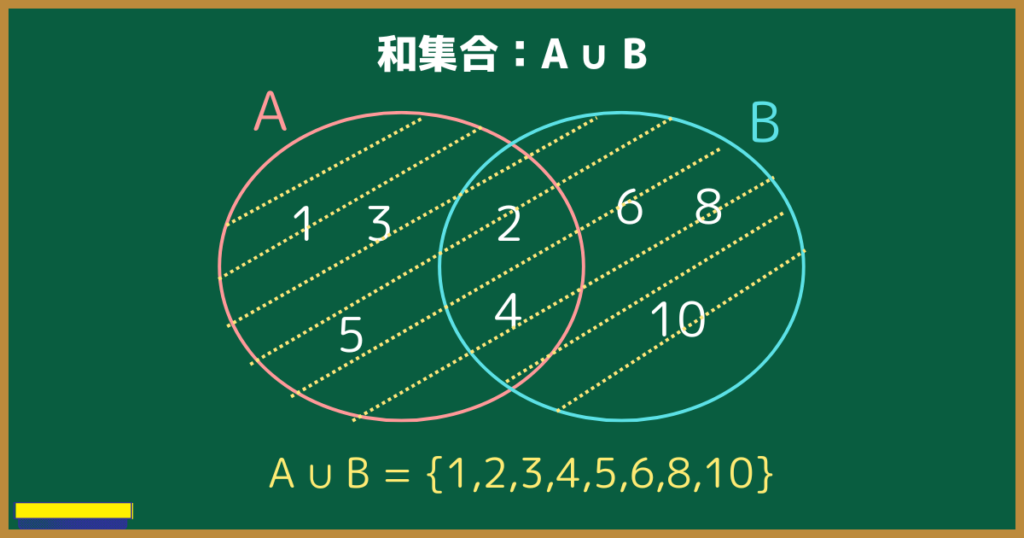
AとBの要素を全て書き並べて、$A \cup B=\{1,2,3,4,5,6,8,10\}$
共通部分『2,4』は1回だけ書く!
ポイントは、共通部分は1回だけ書くことです。
和集合は、図でもイメージできるようにしましょう。
⑧全体集合『$U$』
全体集合とは、問題に出てくるすべての数や文字を集めた集合です。
全体集合の例
1年2組の男子を集合Aとすると、1年2組全員が全体集合$U$にあたる。
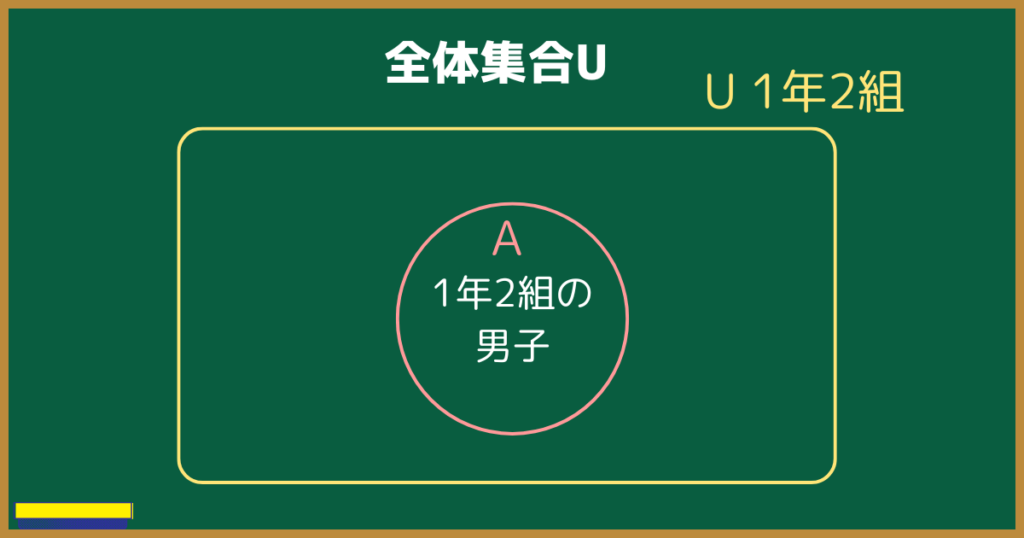

クラスに女子もいるとしたらAに入らないよね?
集合の要素ではないものを集めた集合は補集合と言います。
補集合については、このあとすぐに解説します。
⑨補集合『$\overline{ A }$』
ある集合をAとしたとき、Aに属さない要素を集めた集合を補集合といいます。
補集合の例
全体集合$U=\{1,2,3,4,5,6,7,8,9\}$
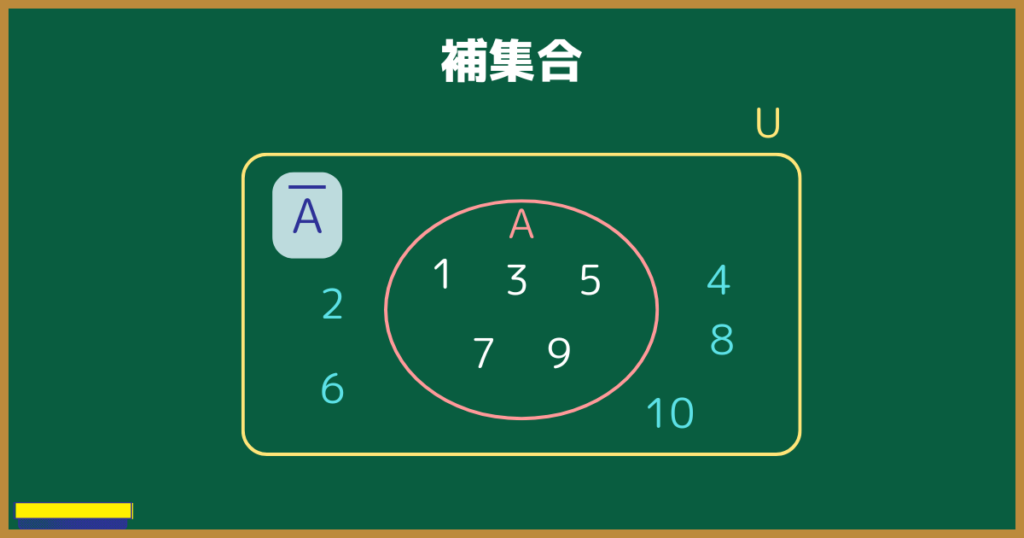
$A=\{1,3,5,7,9\}$のとき、補集合$\overline{ A }$は、
$\overline{ A }=\{2,4,6,8\}$
図で表すと以下のようになる。
集合に出てくる公式を解説
ここからは集合に出てくる公式を解説します。
①ド・モルガンの法則
ド・モルガンの法則は、以下の2種類があります。
ド・モルガンの法則
- $\overline{ A\cap B } = \overline{ A } \cup \overline{ B }$
- $\overline{ A\cup B } = \overline{ A } \cap \overline{ B }$
ド・モルガンの法則を使えば、$ \overline{ A } \cup \overline{ B }$と$ \overline{ A } \cap \overline{ B }$を簡単に求められるのです。
ド・モルガンの法則より$\overline{ A\cap B } = \overline{ A } \cup \overline{ B }$です。
よって$\overline{ A } \cup \overline{ B }$を求めたければ、$\overline{ A\cap B }$を求めればよいのです。
②和集合の個数
和集合の個数を求めるには、以下の計算をします。
和集合の個数
集合Aと集合Bがあるとき、
$n(A \cup B)=n(A)+n(B)-n(A \cap B)$

n(A)+n(B)じゃだめなの?
単にAとBの要素の個数を足しただけだと、AかつBの要素を2回数えてしまいます。
よって、AかつBの要素を1回分ひかなければならないのです。

イメージしずらいな……
集合の個数ではイメージしづらい人は、要素を全て書き並べて考えてみましょう。
和集合の個数を求める例
$A=\{1,2,3,4,5\}$
$B=\{2,4,6,8,10\}$
$A \cup B$の要素を求めるには、$A \cap B$を1回分消さなくてはいけない。
下の画像より、$A \cup B=\{1,2,3,4,5,6,8,10\}$
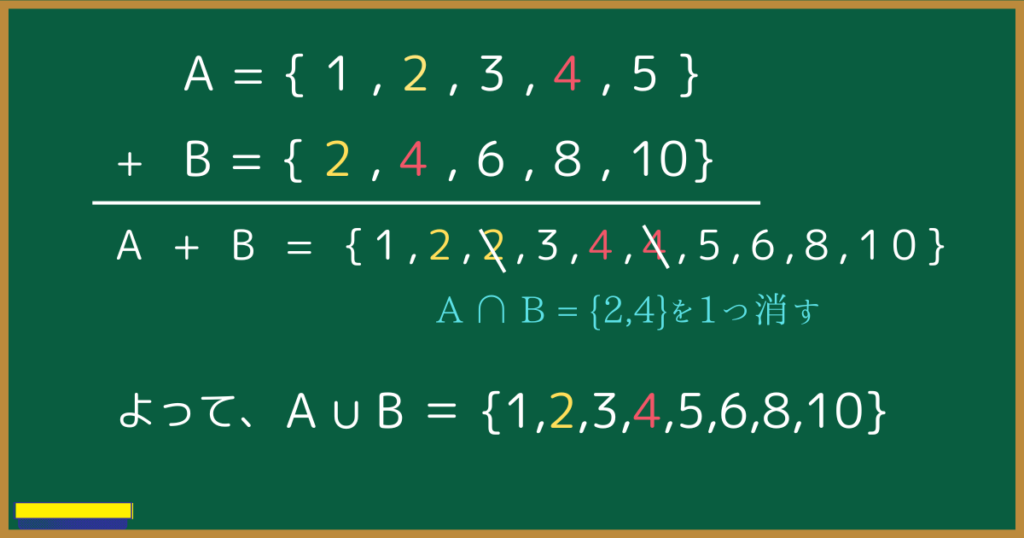
以上のように、和集合を求めるためには単に集合の個数を足すだけでなく、共通部分を引かなければならないのです。
まとめ
ここまで、集合に出てくる用語・記号、公式を解説しました。
聞いたことのない用語や記号がでてきて、混乱してしまうのも無理はありません。
この記事で習ったことを忘れないよう、学校の問題集などで集合の問題を解いて、知識を定着させましょう。

コメントを残す