【中2数学】平行線と角の応用『ブーメラン』の解き方を解説
平行線と角の問題で、いきなりブーメランのような変な形が出てくると混乱してしまいますよね。
この記事では、平行線と角の応用『ブーメラン』性質と、その性質を持つ理由を解説します。
この記事を読めば『ブーメラン』の問題を解けるようになるだけでなく、性質をもつ理由を理解できるので解き方を忘れにくくなります！
平行線と角『ブーメラン』の解き方
まずは平行線と角『ブーメラン』の性質と、なぜその性質をもつのかを解説します。
『ブーメラン』の性質
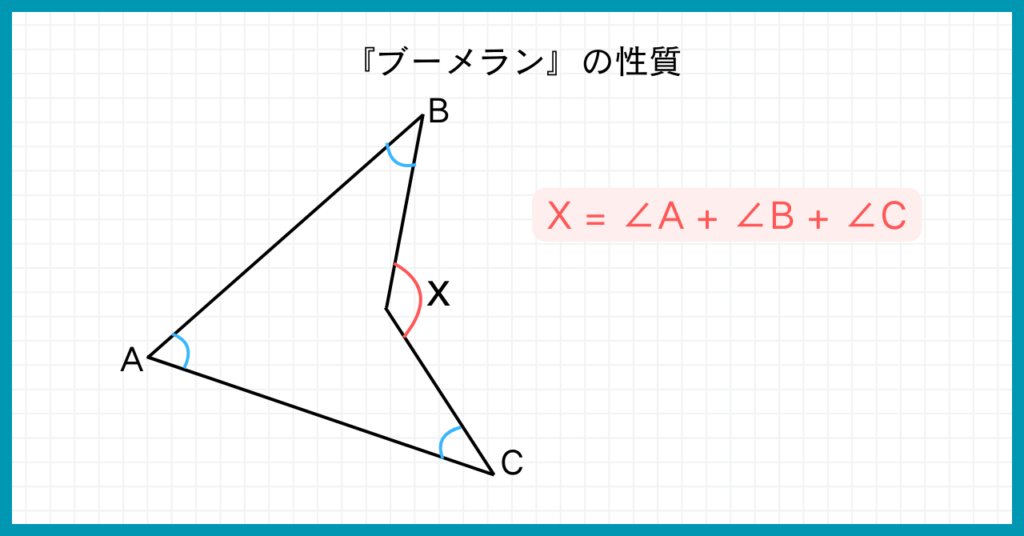
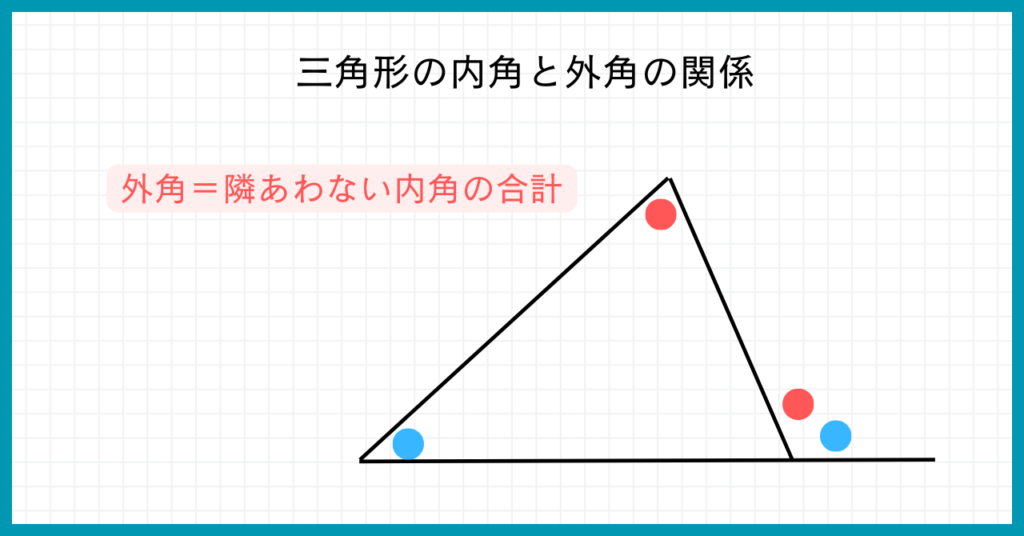
上の図のように、3つの角度を全て足した数が、へこみの部分の角度になります。
【図解】『ブーメラン』の性質が成り立つ理由
ここからは、なぜ『ブーメラン』では3つの角度を全て足した数が、へこみの部分の角度になるのかを確認します。
【前提知識】三角形の内角と外角の関係
三角形の外角＝隣合わない2つの内角の合計
まずはブーメランの図形に、以下のように補助線を引きましょう。
補助線を引くと、上と下に三角形ができますね。
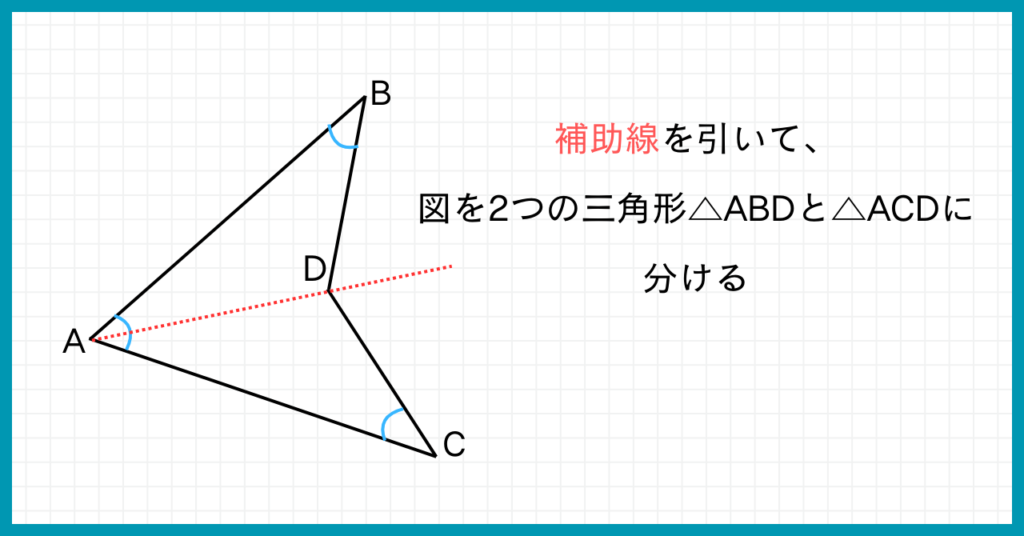
それぞれの三角形について内角と外角の関係より、ブーメランのへこみの部分の角度を表せます。
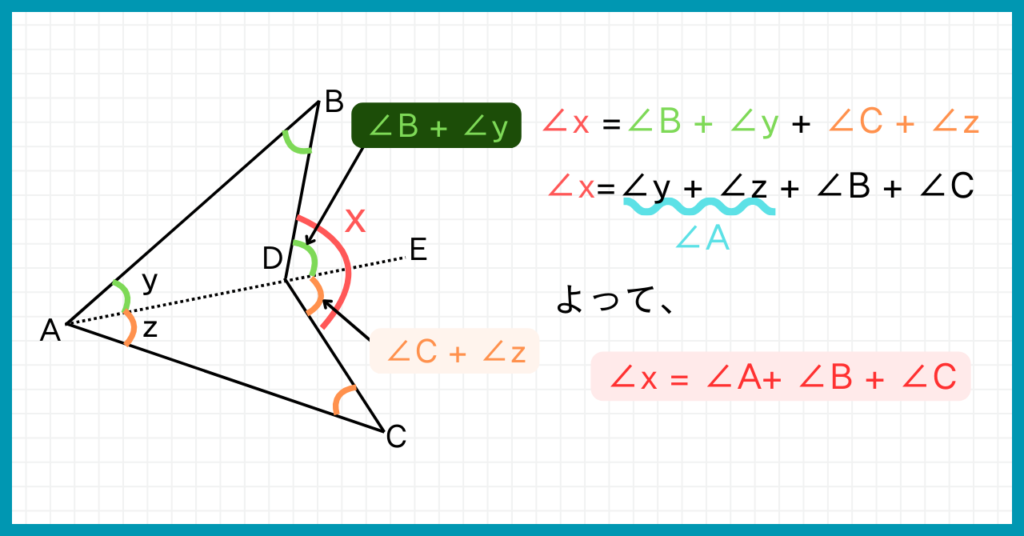
△ABEと△ACD
それが上の図のように表せて、∠x = ∠A+ ∠B + ∠Cとなるのです。
【問題】平行線と角『ブーメラン』
ここからはブーメランの問題を解いてみましょう。
問題
次の図の、xの角度を求めなさい。
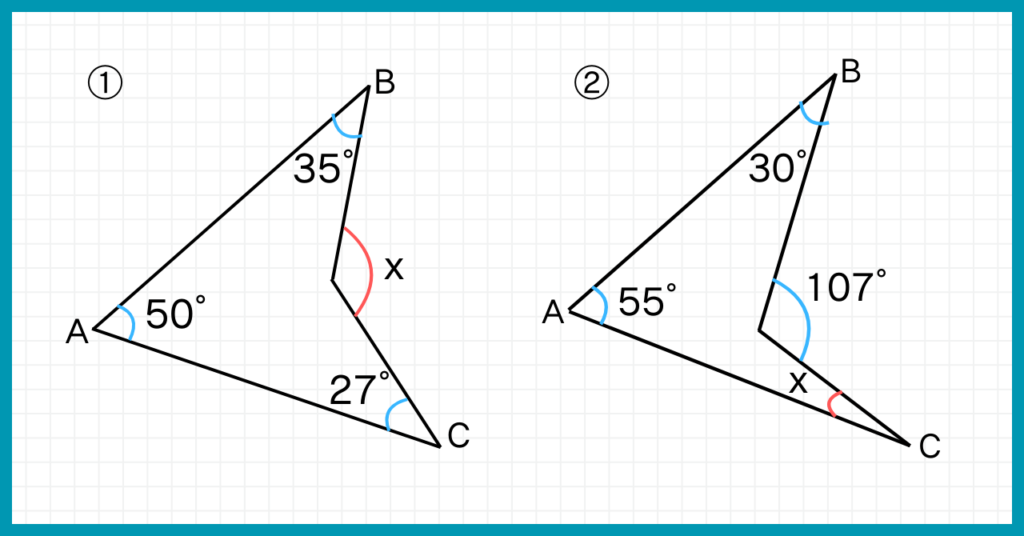
まずは①について。
ブーメランのへこみの部分の角度、つまりxの角度を求めるには、ブーメランの3つの角度を全て足せばよいのでした。
よってxの角度は
50+35+27=112°
②について。
ブーメランの3つの角の合計がへこみの部分の角度なので、それを利用して方程式を作りましょう。
107=55+30+x より
x=22°
まとめ
平行線と角の応用『ブーメラン』は、三角形の内角と外角がわかっていれば簡単に理解できますね。
しかし、なぜ3つの角度を全て足した数がへこみの部分の角度になるのかを理解していないと、解き方を忘れがちになるのでしっかり復習してくださいね。
ブーメランがわかったあなたなら、平行線と角の応用『星形』もすぐに理解できますよ！
もう少し、勉強していきませんか？
コメントを残す