中点連結定理を用いて平行四辺形を証明する方法2パターンを解説

　証明というだけで嫌になってしまうそこのあなた！

　合同ならともかく平行四辺形であること、しかも中点連結定理を用いるとなるとどうやって証明すればよいか想像もできない人が多いことでしょう。

　しかし、中点連結定理を用いて平行四辺形であることを証明する方法は、わかってしまえばとても簡単ですよ。

　この記事では平行四辺形であることを中点連結定理を用いて証明する方法を2パターン解説します。

　やりやすい方を選んで練習して、テストで解答できますよ！

　また、中点連結定理ってなんだっけ？　そもそも平行四辺形の条件ってなに？　というあなたのために、それらも解説しているので安心して読んでくださいね。

【前提】中点連結定理と平行四辺形の条件を覚えていますか？

　中点連結定理を用いて平行四辺形を証明する問題を行う前に、前提知識の確認しましょう。

　①中点連結定理

　②平行四辺形の定義・定理

　以上2つを確認します。

中点連結定理とは

　まずは大前提、中点連結定理とは何かを確認しましょう。

中点連結定理

点Bと点Cがそれぞれ辺ADと辺AEの中点ならば、

BC//DE

$\color{red}{BC=\frac{1}{2}DE}$

　中点連結定理を忘れちゃった、またはもっと詳しく知りたい！という人は以下の記事を読んでくださいね。

平行四辺形の条件

　2年生の時に習った平行四辺形の条件を覚えていますか？

　中点連結定理を用いて平行四辺形を証明する方法は2パターンあります。

　一つは『①2組の対辺がそれぞれ平行』であることを用いて、もう一つは『②1組の対辺が平行で長さが等しい』ことを用いて平行四辺形を証明します。

他の条件についても覚えておいてね！

【例題】中点連結定理で平行四辺形を証明する方法2パターン

　ここからは中点連結定理で平行四辺形を証明する方法を、2パターン解説します。

　以下の例題を用いて、解き方の解説を行います。

例題

　四角形ABCDにおいて、点E、点F、点G、点Hがそれぞれ辺AB、辺BF、辺CD、辺ADの中点であるとき、四角形EFGHが平行四辺形であることを証明しなさい。

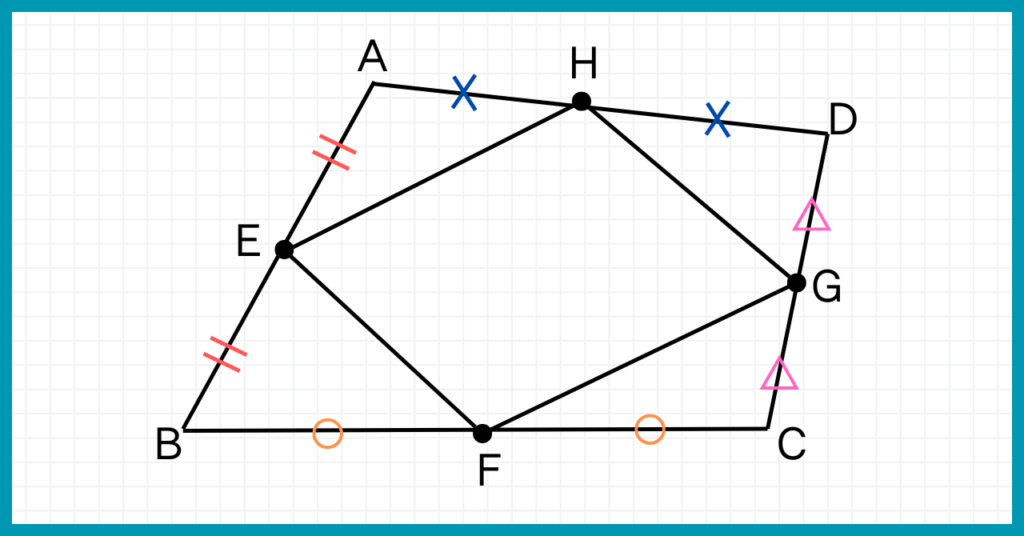
①2組の対辺がそれぞれ平行

　まずは『①2組の対辺がそれぞれ平行』であることを示す方法を解説します。

　まず、図にはたくさんの中点があるので、中点連結定理を使えないかな？　と考えましょう。

でも、三角形がないと中点連結定理が使えないよ？

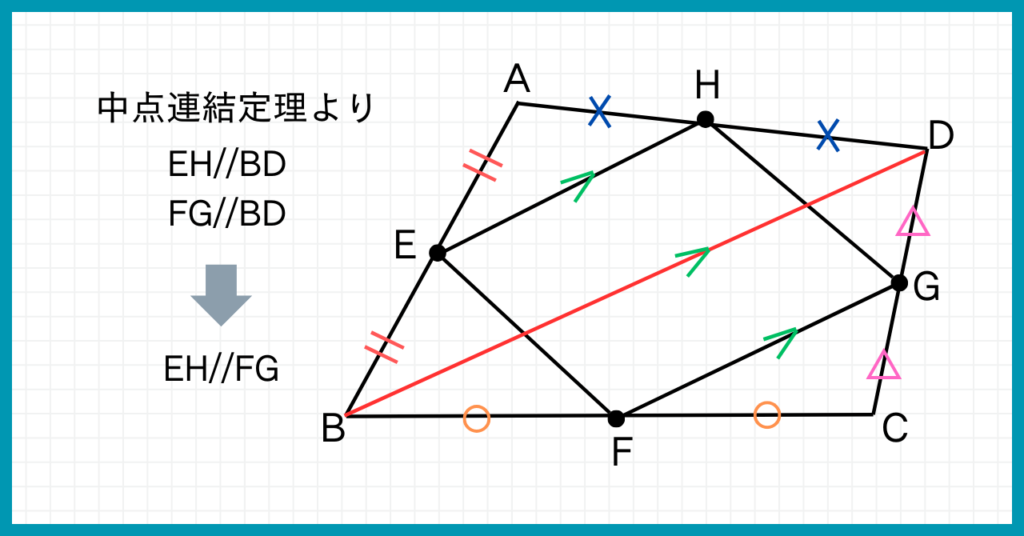
　そこで、BDに補助線を引いてみましょう。

　すると、△ABDと△CBDが出現します！

　まずは△ABDについて見ていきましょう。

　点Eが辺AB、点Hが辺ADの中点なので、△ABDについて中点連結定理を適用できます。

　よって、EH//BDです。

　次に△CBDについて見て見ると、点Fが辺BC、点Gが辺CDの中点なので、△CBDでも中点連結定理を適用できます。

　よって、FG//BD

　以上よりEH//BDかつFG//BDなので、EH//FGとなります。

　さらに、ACに補助線を引きます。

　すると△ABCと△ADCが出現しますね。

　同じように△ABCと△ADCについて中点連結定理を適用すると、

　△ABCよりEF//AC

　また△ADCよりHG//AC

　以上よりEF//ACかつHG//ACなので、EF//HGとなります。

　EH//FGかつEF//HGより、2組の対辺がそれぞれ平行なので、四角形EFGHは平行四辺形であるといえます。

　以下、解答をまとめます。

②1組の対辺が平行で長さが等しい

　中点連結定理を用いて平行四辺形を証明する方法はもう一つあります。

　ここからは『②1組の対辺が平行で長さが等しい』ことを用いて証明していきます。

　改めて問題を出しておきますね。

例題

　四角形ABCDにおいて、点E、点F、点G、点Hがそれぞれ辺AB、辺BF、辺CD、辺ADの中点であるとき、四角形EFGHが平行四辺形であることを証明しなさい。

　BDに補助線を引き、△ABDと△CBDを作ります。

　そのあとで中点連結定理を用いて、EH//FGを示すところまでは『①2組の対辺がそれぞれ平行』の方法と同じです。

　ここからが『②1組の対辺が平行で長さが等しい』ことを示す方法です。

　EH//FGを示したあとで、EF=FGを示します。

　△ABDにおいて中点連結定理を適用すると、$EH=\frac{1}{2}BD$

　また△CBDにおいて中点連結定理を適用すると、$FG=\frac{1}{2}BD$

　つまりEH=FGですね。

　よってEH//FGかつEH=FGより1組の対辺が平行で長さが等しいので、四角形EFGHは平行四辺形であるといえます。

　以下で解答をまとめます。

まとめ

　この記事ではまず中点連結定理と平行四辺形の条件を確認しました。

　そのあとで、中点連結定理を用いて平行四辺形を証明する方法として『①2組の対辺がそれぞれ平行』と『②1組の対辺が平行で長さが等しい』を示す解き方を解説しました。

　中点連結定理を用いた証明なので、難しそうに感じていた人がいるかもしれません。

　しかし、補助線を引くことさえ覚えてしまえばあとは簡単でしたよね。

　とはいえ復習しないと忘れてしまうので、自力で解けるように問題演習を忘れずに行ってくださいね。