【基礎】中点連結定理の公式と使い方を詳しく解説【中3数学】

平行線と比の公式を理解できていれば、新たに暗記するまでもなく中点連結定理の公式を覚えられます。
中点連結定理の難しさは公式の暗記ではなく、中点連結定理の公式を利用できるように工夫をすることなのです。
さて、あなたは中点連結定理の公式を使いこなせているでしょうか?
この記事では、中点連結定理の公式を解説したあと、中点連結定理を用いた基本的な問題を行います。
公式だけでなくその成り立ちも解説しているので、公式を丸暗記せずに理解できます。
また問題演習の前に、中点連結定理の使い方も解説しているので、中点連結定理を用いた応用問題を解く際にも役立ちますよ!
中点連結定理とは
まずは中点連結定理を確認しましょう。
中点連結定理が成り立つ理由
ここからは中点連結定理を丸暗記しなくて良いように、中点連結定理より
①BC//DE
②$BC=\frac{1}{2}DE$
の2つが成り立つ理由を解説します。
【前提】2つの三角形が相似であることから成り立つ
中点連結定理の公式に出てくる三角形、見覚えがありますよね?
そうです。平行線と比の公式でも出てきました。
中点連結定理の公式も平行線と比の公式と同じように、2つの三角形が相似であることから成り立っています。
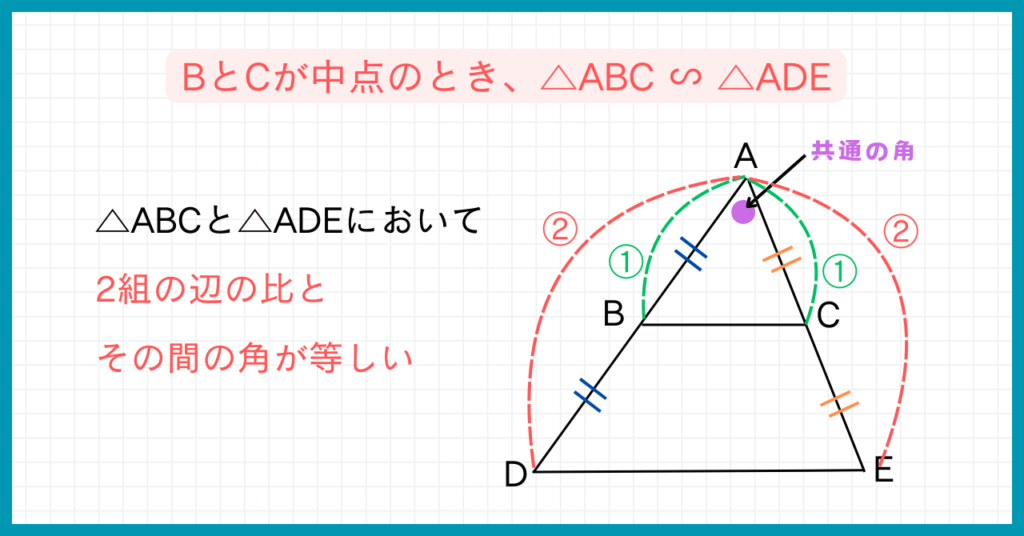
下の図を見ると、点Bと点Cがそれぞれ辺ADと辺AEの中点なので、△ABC∽△ADEが成り立ちますよね。
BC//DEが成り立つ理由
これまでで△ABC∽△ADEであることを解説しました。
相似な三角形の対応する角は等しいので、下の図のように辺BCと辺DEにおいて同位角が成り立ちます。
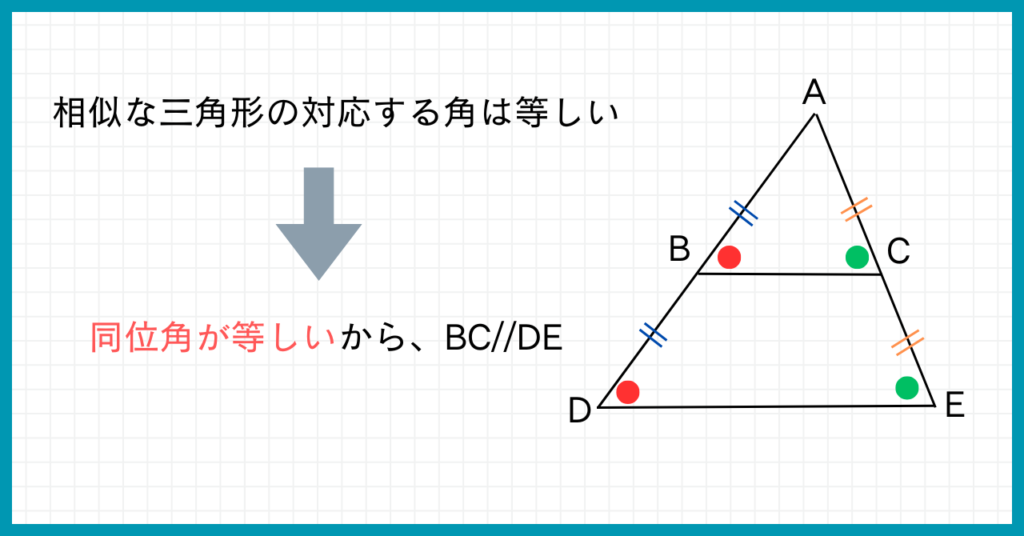
同位角が成り立つということはBC//DEであるということです。
$BC=\frac{1}{2}DE$が成り立つ理由
点Bと点Cはそれぞれ辺ADと辺AEの中点なので、AB:BD=AC:CE=1:1
つまりAB:AD=AC:AE=1:2なので、△ABCと△ADEの相似比は1:2です。
よって相似な図形の対応する辺の比は等しいので、BC:DE=1:2となります。言い換えると、BCはDEの半分の長さになるのです。
よって、$\color{red}{BC=\frac{1}{2}DE}$が成り立ちます。

【基礎】中点連結定理の利用
ここからは中点連結定理を利用する問題を行います。
まずは中点連結定理の使い方を確認しましょう。
中点連結定理の使い方
中点連結定理といえば、中点、そして三角形です。
図形の中にそれらが出ていれば、中点連結定理を使えないかを考えましょう。
中点連結定理を用いる問題は、台形や平行四辺形と一緒に出てきます。

でも台形も平行四辺形も、三角形じゃないよ?
中点連結定理は三角形じゃないと使えないよね?
そんなときは、図形に補助線を引いて三角形を作り、中点連結定理を使うのです!
このあとで、補助線を引いて三角形を作り中点連結定理を使う問題を行います。
【問題】中点連結定理を用いて辺の長さを求める
問題
台形ABCDがある。点Eと点FはそれぞれABとDCの中点であり、AD//EFで、EF//BCである。
AD=10cmでBC=16cmのとき、EFの長さを求めなさい。

問題文中に、中点が出てきましたね。

中点が出てきたということは、中点連結定理が使えないかを考えるんだね!
中点連結定理を使うには、補助線を引いて三角形を作るのでした。
以下のように補助線を引いてみましょう。

点Aと点Cを結ぶと、台形ABCDの中に△ABCと△CADが出現したではありませんか!
△ABCと△CDAに対して中点連結定理をすると、EFの長さを求められます。
このとき補助線とEFの交点をGとすると、
△ABCでEG、△CDAでFGの長さを求められるので、
EF=EG + FG
をすれば良いのです。
以下、解答です。
解答

AからCに向かって補助線を引き、補助線とEFとの交点をGとする。
△ABCにおいて、中点連結定理より
$EG=\frac{1}{2}×16$
$EG=8$
また△CDAにおいて、中点連結定理より
$FG=\frac{1}{2}×10$
$FG=5$
よってEF=EG+FGなので
EF=13cm
まとめ
中点連結定理を利用する問いは、公式そのものを用いて計算するよりも中点連結定理を用いられるよう工夫をするのが難しいところです。
中点連結定理の公式だけでなく、それを図形の中でどうやって使うのか意識しながら問題演習を行ってくださいね。


コメントを残す