【図解】円柱の表面積の求め方3ステップを解説！裏技公式も紹介

　円柱の体積を求めるのは簡単でも、表面積を求める方法はなかなか理解できない人がいることでしょう。

　特に、円柱の側面積を求めるために、底面の円の円周を用いる方法がわかりにくいですよね。

　この記事では円柱の表面積の求め方を解説します。

　特に難しい『側面積の求め方』を図を用いて解説しているので、図形が苦手な人でも安心して読んでくださいね。

　また、学校で習うやり方だけでなく、覚えておくと便利な『円柱の表面積を求める裏技公式』も紹介しています。

【学校で習う】円柱の表面積の求め方

　まずは学校で習う円柱の表面積の求め方を解説します。

　円柱の表面積は次の3ステップで求めます。

• 展開図を描く
• 長方形の横＝円周
• (円の面積×2+長方形の面積)で円柱の表面積を求める

　次の例題を用いて解説します。

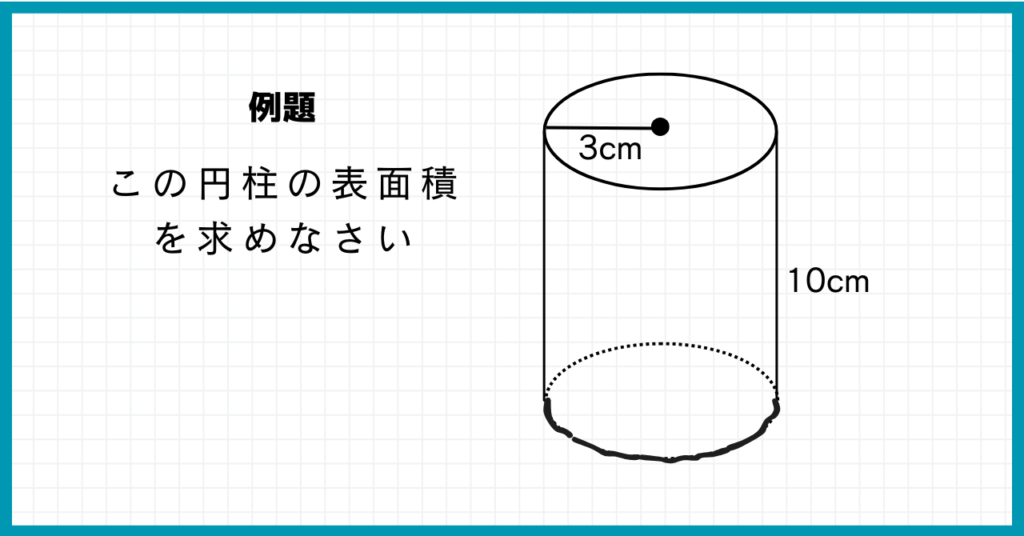
例題

　底面の円の半径が3cm、高さが10cmの円柱がある。

　この円柱の表面積を求めよ。

【STEP1】展開図を描く

　円柱の表面積を求めるため、まずは円柱の展開図を描きましょう。

　慣れてきたら、省略しても構いません。

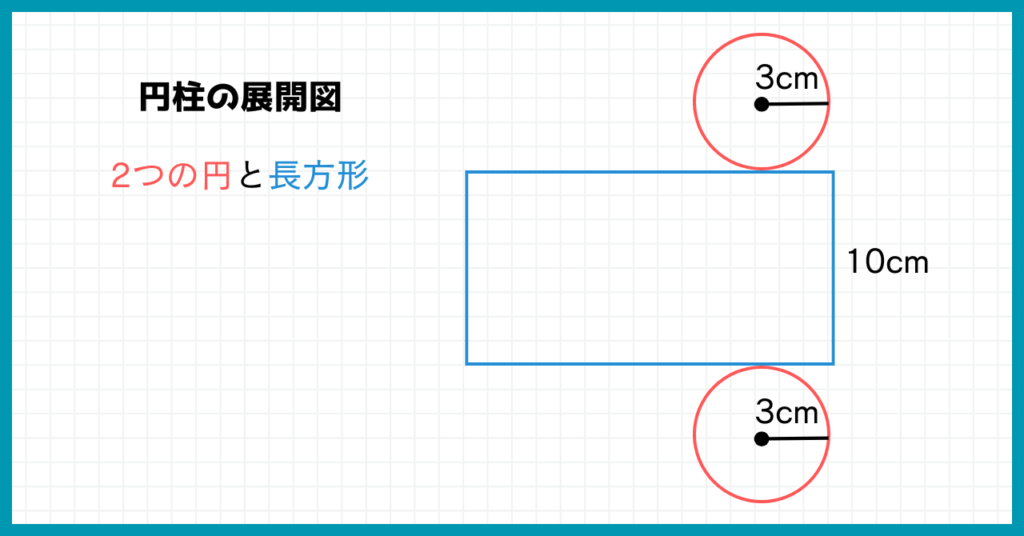
　円柱の展開図を描くと、円柱は2つの円と1つの長方形でできているのがわかりますね。

円柱の表面積は『2つの円の面積+1つの長方形の面積』で求められるんだね！

【STEP2】長方形の横＝円周

　円柱の表面積を求めるために、2つの円の面積と1つの長方形の面積をそれぞれ求めます。

　円の面積は、半径がわかっているので問題ないでしょう。

　そうなると問題は、長方形の部分(円柱の側面積)です。

長方形の縦の長さは円柱の高さと同じだね。

でも長方形の横の長さがわからないよ？

　この長方形は円柱の側面積ですよね。

　長方形の横の部分は底面の円周とぴったり重なっているので、円周の長さを求めれば長方形の長さがわかります！

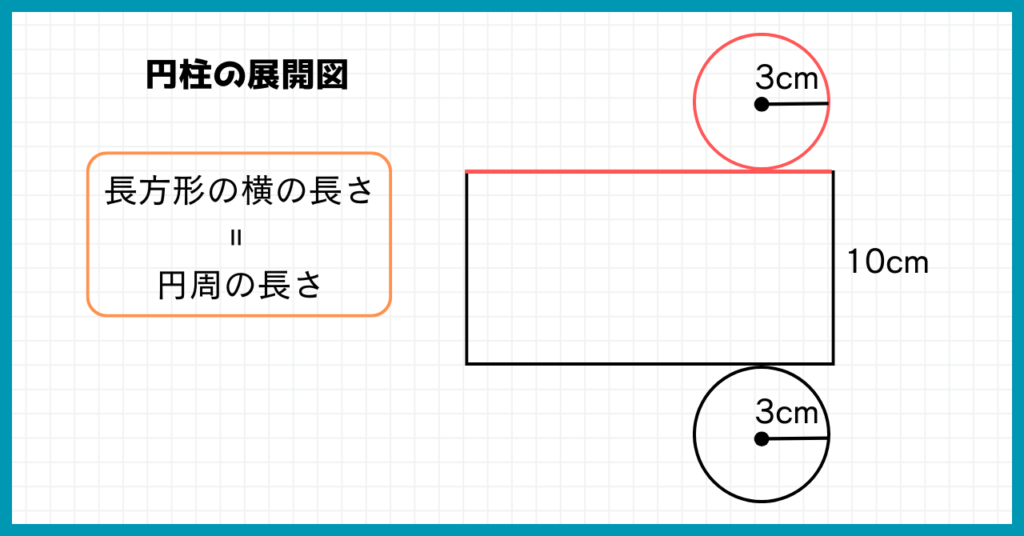
　円の半径が3cmなので、円周の長さは

　$2×π×3$

　$=6π(cm)$

【STEP3】(円の面積×2+長方形の面積)で円柱の表面積を求める

　さて、STEP2で長方形の横の長さがわかったので、いよいよ円柱の表面積を求められます。

円柱の表面積は、

円の面積2つと、側面の長方形の面積を足せばいいね！

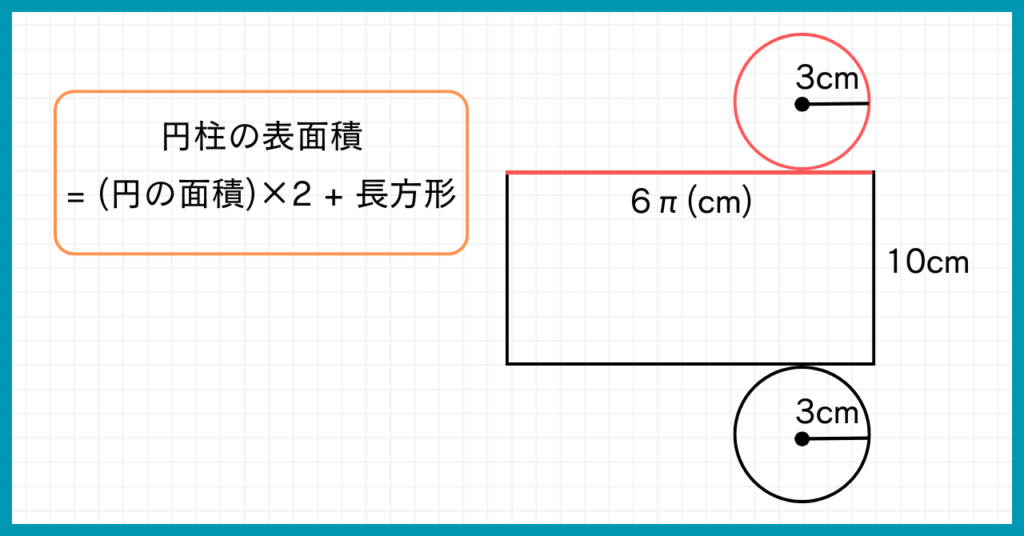
　では、計算していきましょう。

　(円の面積)×2+長方形の面積

　$3×3×π×2+10×6π$

　$=78π$

　よって答えは$\color{red}{78π(cm^2)}$

【裏技】円柱の表面積を求める公式

　ここまでは教科書に載っている、基本的な解き方を解説しました。

　でもこの解き方、ちょっと大変でしたよね？

もっとラクに円柱の表面積を求める方法、ないかなー。

　あるんです実は！

　これで、上の例題を解いてみましょう。

例題

　底面の円の半径が3cm、高さが10cmの円柱がある。

　この円柱の表面積を求めよ。

　$S=2πr(r+h)$だから、

　$S=2π×3×(3+10)$

　$=6π×13$

　$=78π(cm)$

　基本的な解き方と答えが同じになりましたね。

まとめ

　円柱の表面積を求める基本的な方法は、説明をよく読めばわかりやすいですよね。

　しかし、円柱の表面積を求めるには公式を用いた方が便利だと思いますよね。

　公式を覚えるとラクに問題を解けますが、公式は忘れるリスクがあります。

　基本的な解き方を理解した上で、公式での解き方に挑戦してくださいね。