【図解】ユークリッドの互除法の計算方法と原理をわかりやすく解説

　ユークリッドの互除法を用いた問題を解くには、まずはその計算方法を暗記しなければいけませんよね。

　ユークリッドの互除法は計算方法が複雑な上に計算自体も面倒なため、せっかく丸暗記してもすぐに忘れてしまいます。

　なぜユークリッドの互除法の計算をすぐに忘れてしまうのか。

　それは、あなたがユークリッドの互除法とは何かを理解していないからです。

そもそもユークリッドの互除法ってなに！？

　ユークリッドの互除法が何かを理解していればユークリッドの互除法の原理がわかり、原理がわかれば計算方法を忘れにくくなります。

　この記事では、ユークリッドの互除法の計算方法とその原理を解説します。

ユークリッドの互除法とは『最大公約数を求める方法』のこと

　ユークリッドの互除法を一言で言うと、『最大公約数を求める方法』です。

　ユークリッドの互除法でおなじみの$a=bq+r$の式を用いて最大公約数を求めるわけですよね。

　これが何の式かわかりますか？

$a=bq+r$は、

$(割られる数)＝(割る数)×商+余り$

のことだね！

　つまりユークリッドの互除法とは、小学校でも習った$(割られる数)＝(割る数)×商+余り$の式を使って、最大公約数を求める方法ということです。

　では、なぜ$(割られる数)＝(割る数)×商+余り$の式で最大公約数が求められるのか。

　それは、この式には以下のような関係があるからです。

　$a=bq+r$で、$a=224，b=160$として、qとrを求めてみると以下のようになります。

　$224=160×1+64$

　上の画像の式に当てはめて考えてみると、224と160の最大公約数と160と64の最大公約数は同じになります。

　それなら、224と160の最大公約数よりも、数の小さい160と64の最大公約数を求めた方が簡単そうですよね。

でもそれなら

$160=64×2+32$として、

160と64の最大公約数よりも

64と32の最大公約数を求めた方が簡単！

　このような考え方で、最大公約数を求める2つの数をどんどん小さくしていくのがユークリッドの互除法での最大公約数の求め方なのです！

　では、ユークリッドの互除法で224と160の最大公約数を求めてみましょう。

なぜユークリッドの互除法が成り立つのかを解説

　これまではユークリッドの互除法で最大公約数を求められることをお話してきました。

　ここからは、なぜ$a = b q + r$で、a と b の最大公約数はb と r の最大公約数と同じになるのかを解説します。

小学校の復習『長方形に敷き詰める正方形』

　ユークリッドの互除法の原理を解説する前に、次の問題を解いてみてください。

　ユークリッドの互除法の原理を理解するためには、この問題が解けなくてはなりません。

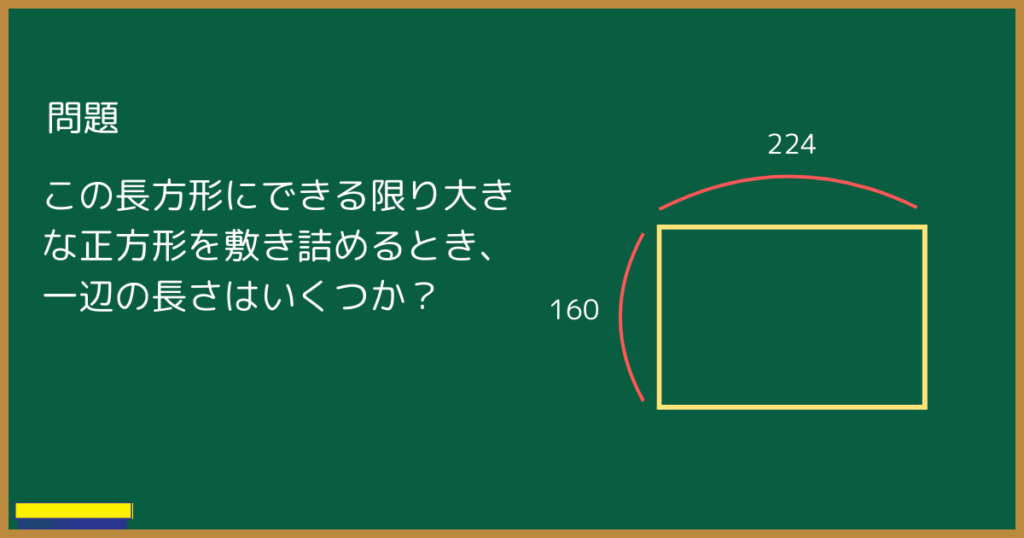
　長方形の中に正方形を敷き詰める問題は、実は小学校の時に習っています。

縦と横の最大公約数を求めればいいね！

　224と160の最大公約数は32です。

　つまり、横が224、縦が160の長方形を敷き詰められる正方形の中で、一番大きな正方形の一辺の長さは32です。

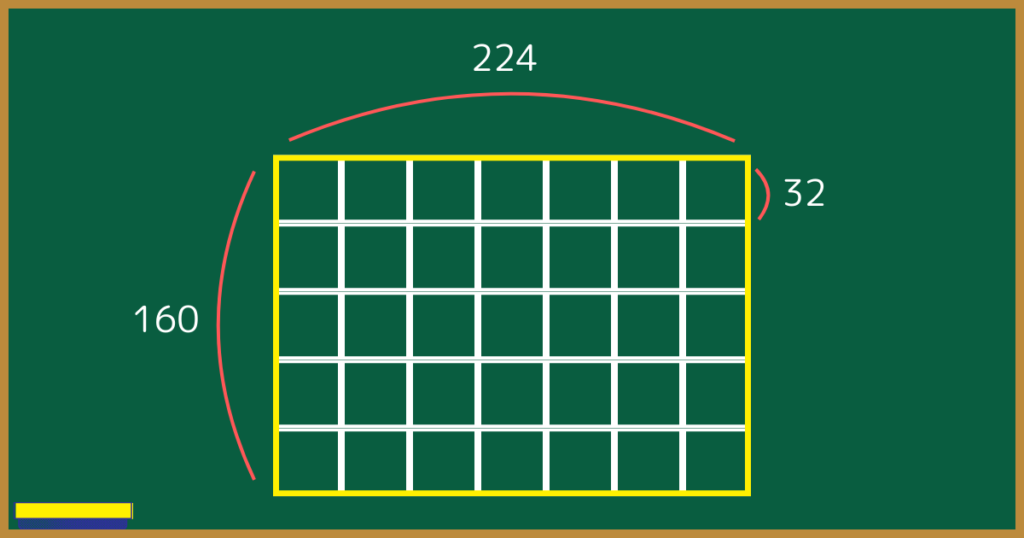
ユークリッドの互除法の原理

　224と160の最大公約数が32であることがわかった上で、改めて求めてみましょう。

　ユークリッドの互除法で224と160の最大公約数を求めるとき、まずは以下の式を書きますよね。

$224＝160×1+64$

この式を作ることによって、

224と160、160と64の最大公約数が同じであることがわかるんだよね。

　以上のことを図で表してみましょう。

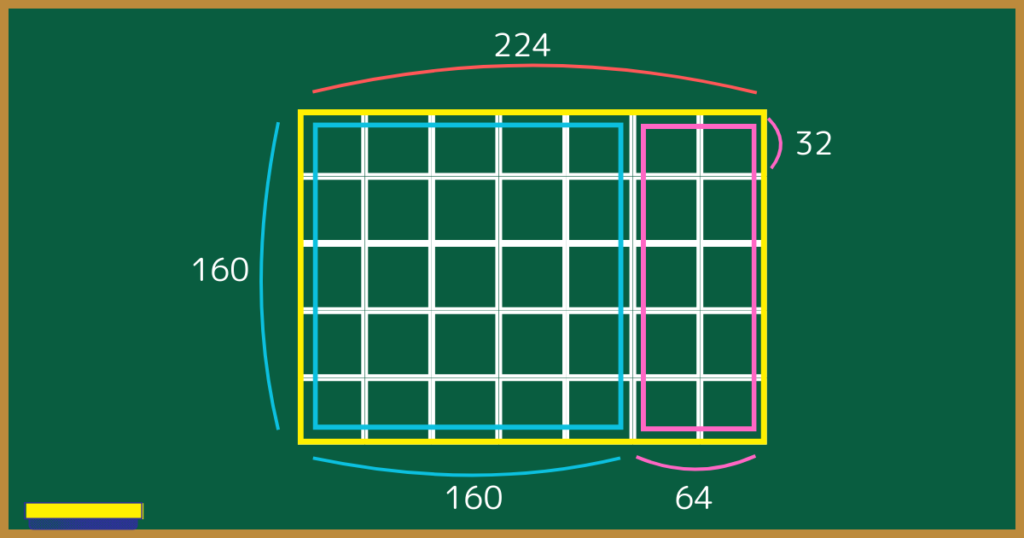
　$224＝160×1+64$と表されるとき、224と160、160と64の最大公約数が同じであることがわかります。

　これは、160×224の長方形の中に160×64の長方形ができ、2つの長方形の中にできる正方形の一辺の長さが等しいことから説明できます。

　長方形の中にできる正方形の一辺の長さはつまり、最大公約数のことですよね。

　以上のように、ユークリッドの互除法の原理は、小学校で習った『図形と最大公約数の関係』で説明がつくのです。

まとめ

　ユークリッドの互除法は最大公約数の求める方法です。式を用いて最大公約数を求める2つの数をどんどん小さくし、最大公約数を求めやすくしていきます。

　ユークリッドの互除法で最大公約数を求める原理は、小学校で習った『図形と最大公約数の関係』で説明ができます。ポイントは、正方形の一辺の長さ(＝最大公約数)が変わらないことでした。

　ユークリッドの互除法は計算方法が複雑に見えるので、あなたは苦手に感じてしまったのでしょう。

　しかし、算数を知っていれば理解できる内容ですので、複雑な見た目に怯まず、ユークリッドの互除法の問題にチャレンジしていきましょう。