【中高生必見】二次関数の概形を描くときのポイント4選+2を解説

　数学の授業で、二次関数のグラフを描いて問題を解くよう指導されるかもしれません。

　しかし、方眼紙に定規を使って書く方法は知っていても、問題を解く途中でグラフの概形(がいけい)を描くにはどうしたら良いか分からないという人がいるのではないでしょうか。

　この記事では二次関数のグラフの概形を描くときのポイントを解説します。

　このポイントさえ押さえれば、二次関数のグラフの概形を描き、スムーズに問題を解けるようになりますよ！

二次関数のグラフの概形を描くのが重要な理由

　一次関数でも二次関数でも、関数の問題ではグラフを描かないと問題文で言われている状況がわかりません。

　図形の問題だって、問題文中に示された条件を元に図形を描きますよね？

　それと同じように、関数のグラフも描かないと問題文を正しく理解することができないのです。

　例えば二次関数の変域を求める問題で、xの変域からyの変域を求める問題です。

　xの変域が0をまたぐか否かによって、yの変域は少し考えなくてはいけませんよね。

　中学で習う二次関数ぐらいなら、まだグラフを描かずに対応できるかもしれません(おすすめはしませんが)。

　しかし、高校ではそうはいきません。

　グラフの概形を描けないと、まず問題を解けません。

　中学にせよ高校にせよ、問題文を読み取りグラフの概形が描けないのであれば、問題の本質を理解して問題を解けているとは言いがたいので、グラフの概形を描けるようにしておきましょう。

二次関数のグラフの概形を描くポイント4選+2

　二次関数$y=ax^2$のグラフを描くにはいくつかポイントがあります。

• aが正の数なら下に凸、負の数なら上に凸
• aが大きければ大きいほど幅が狭くなり、小さければ小さいほど幅が広くなる
• 座標は比率を意識する
• 変域の端を含むなら黒丸、含まないなら白丸を描く
• 【高校生】軸と頂点を描く
• 【高校生】x切片、y切片を求める

　①～④は全員共通で必要な内容です。

　⑤と⑥は高校生の内容なので、中学生は読み飛ばしてOKです。

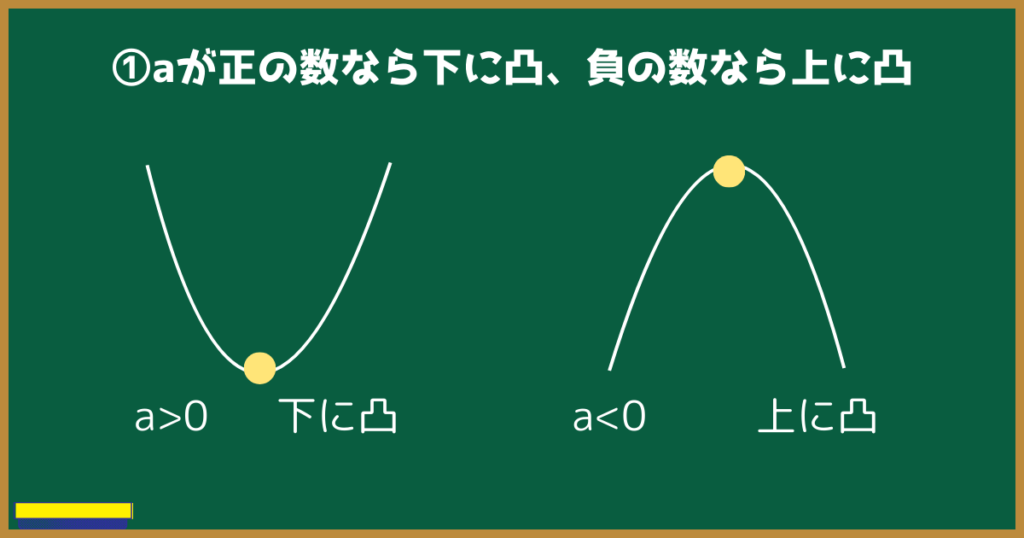
①aが正の数なら下に凸、負の数なら上に凸

　二次関数$y=ax^2$のaの正負で、グラフの向きを決めます。

　aが正の数なら下に凸(とつ)、負の数なら上に凸(とつ)です。

　凸(とつ)とは二次関数の閉じた部分のことです。

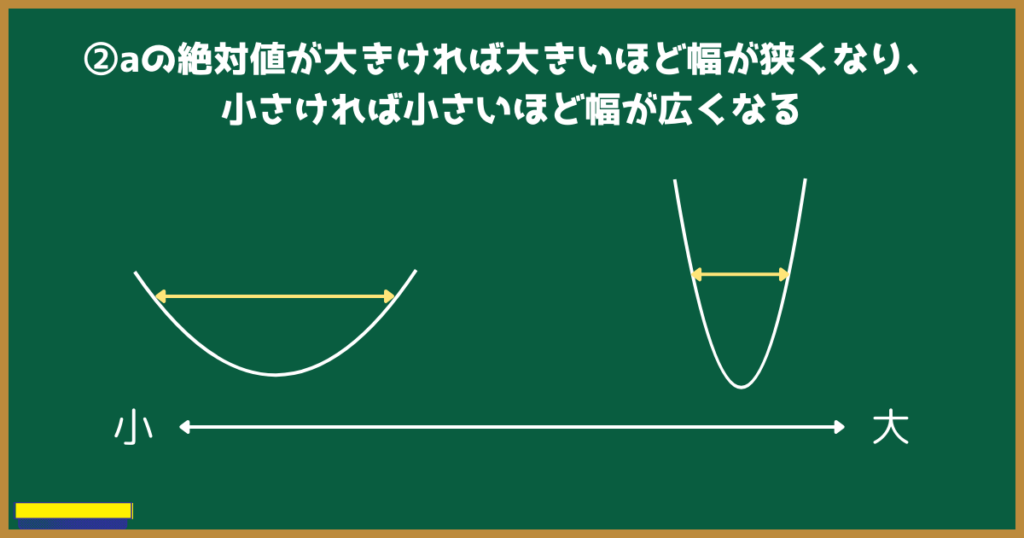
②aの絶対値が大きければ大きいほど幅が狭くなり、小さければ小さいほど幅が広くなる

　二次関数$y=ax^2$のaの絶対値で、グラフの幅を決めます。

　aの絶対値が大きければ大きいほど幅が狭くなり、小さければ小さいほど幅が広くなるのです。

　例えば$y=2x^2$と$y=-3x^2$では、どちらの方が幅が狭いでしょうか？

aの絶対値が大きいのは$y=-3x^2$だから、

$y=-3x^2$の方が幅が狭いね！

　幅を決めるコツは、aが1より大きいか小さいかを見ることです。

　aが1より大きければ幅を狭く、小さければ幅を広くすることを意識しましょう。

③座標は比率を意識する

　グラフの概形を描くときに、座標も描くことがあるでしょう。

　特に変域を描くことは多くあります。

　例えば$y=x^2$のグラフを$-1<x≦2$で描くときはどうなるか。

　このときxの変域の両端であるx=-1とx=2、すなわち座標(-1,0)と(2,0)を書き入れることになります。

　さてあなたは、座標(-1,0)と(2,0)の原点からの距離を意識しましたか？

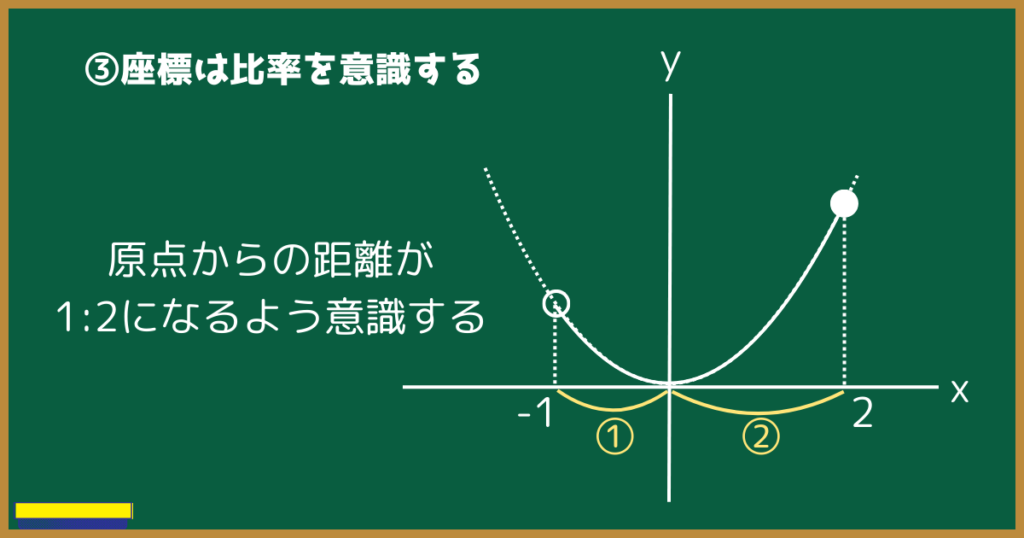
　x軸を数直線とみると、座標(-1,0)と(2,0)の原点からの距離の比は1:2になりますよね。

　方眼紙に描いたような正確なグラフは必要はありませんが、目測で明らかに1:2に見えないグラフはNGです。

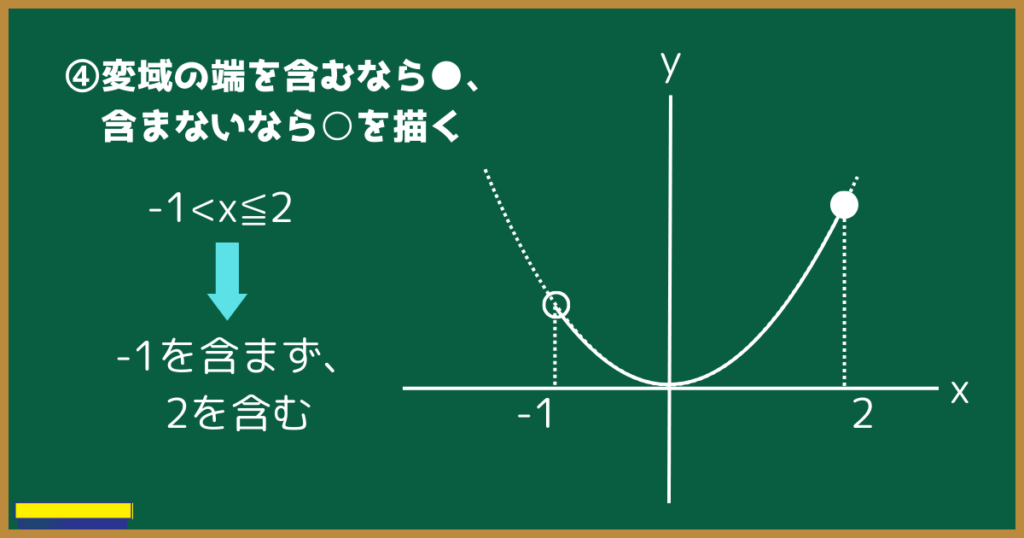
④変域の端を含むなら黒丸、含まないなら白丸を描く

　数学の授業などで先生が何気なく描いているであろう、グラフの○や●の意味をわかっていますか？

　○や●は、変域の両端を示しています。

　2つの違いは、端の数を含まないなら○、含むなら●を描くことです。

　例えば$-1<x≦2$は、-1を含まず、2を含むということです。

　$y=x^2$のグラフを$-1<x≦2$で描くとき、-1は○で、2は●を描きます。

【高校生】⑤軸と頂点を描く

　高校生は上で紹介した①～④のポイントに加えて、⑤と⑥のポイントも勉強しましょう。

　軸と頂点がある二次関数のグラフでは、概形を描くときに始めに軸と頂点を求めましょう。

　軸と頂点がわかれば第何象限にグラフがあるのかがわかるので、概形を描きやすくなりますよ。

　x切片、y切片を求める

【高校生】⑥x切片、y切片を求める

　軸と頂点があるということはx軸やy軸と交点ができます。よって、必要であればx切片、y切片を求めましょう。

　ただし問題によっては必要ないこともあります。

　x切片、y切片の具体的な求め方は以下の例題で示します。

【実践】二次関数のグラフの概形を描いてみよう

　これまでの内容を活かして、グラフの概形を描いてみましょう。

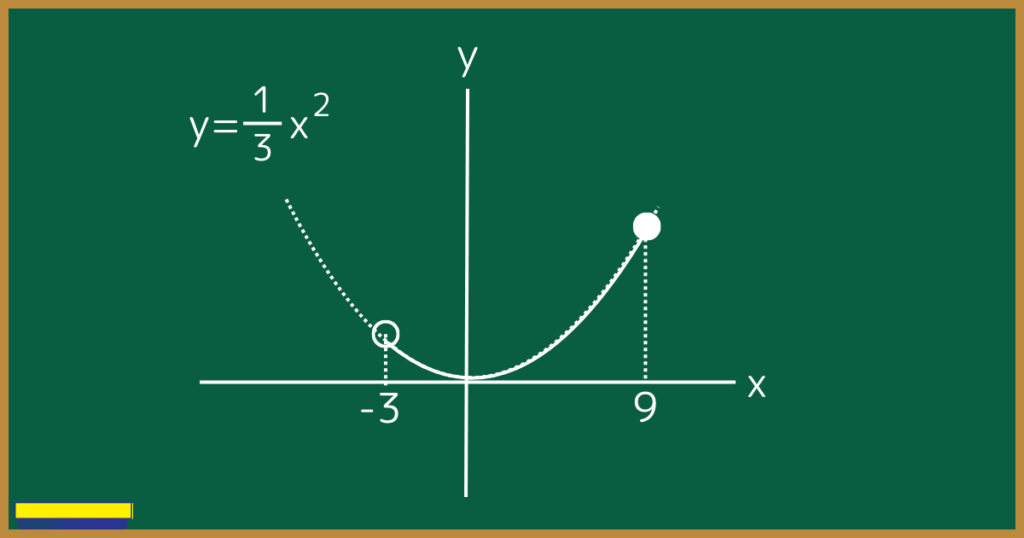
　①について。

　$y=\frac{1}{3}x^2$はaが正の数なので下に凸です。

　また、aの絶対値が1よりも小さいので、幅を広めに描きましょう。

　さらに変域が$3<x≦9$より3を含まず9を含むので、3を○、9を●にします。

　②について。

　$y=-3x^2$はaが負の数なので上に凸です。

　また、aの絶対値が1よりも大きいので、幅を狭めに描きましょう。

　さらに変域が$-1≦x<3$より-1を含み3を含まないので、-1を●、3を○にします。

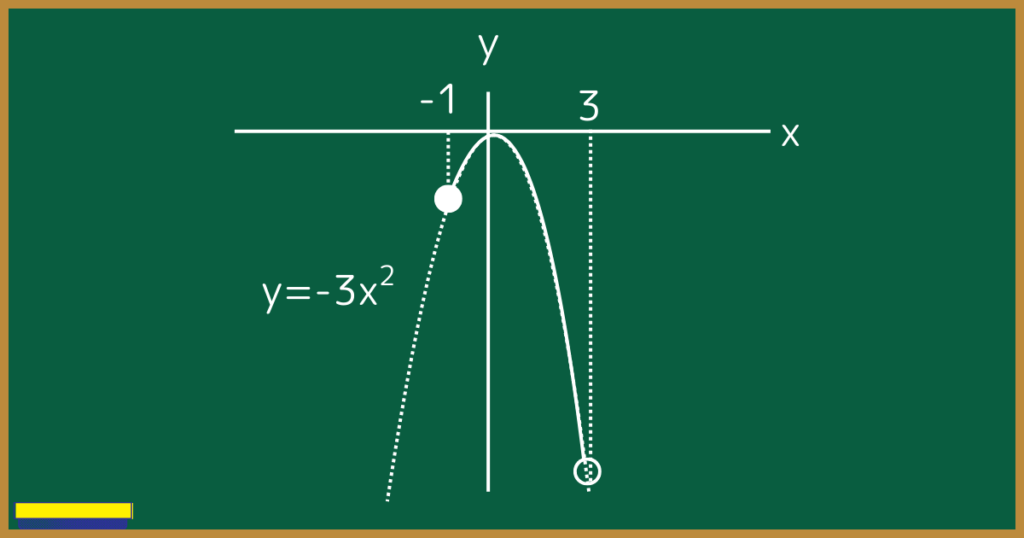
　③について。

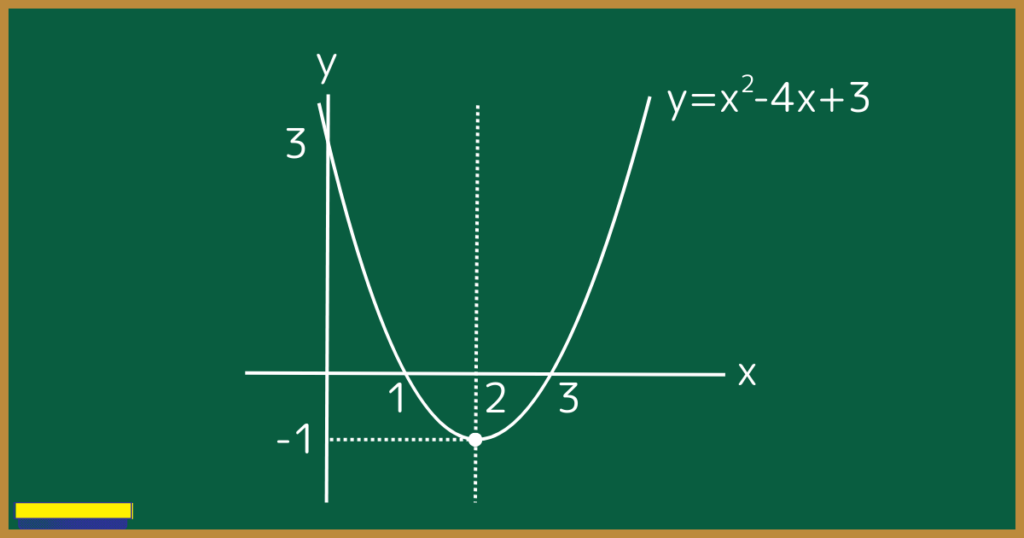
　軸と頂点があるので、まずはそれらを求めます。

　軸と頂点を求めるには、平方完成をするんでしたね。

　$y=x^2-4x+3$
　$y=(x-2)^2-1$

　軸はx=2で、頂点は(2,-1)です。

　次に、x切片とｙ切片を求めましょう。

　x切片はy=0なので、$0=x^2-4x+3$としてxの値を求めます。

　$0=x^2-4x+3$
　$(x-1)(x-3)=0$
　$x=1,3$

　さらにy切片はx=0なので、$y=x^2-4x+3$よりy=3です。

　よってx切片はx=1,3で、y切片はy=3です。

　最後にグラフの向きと幅です。

　$y=x^2-4x+3$は$y=ax^2+bx+c$の形です。

　x^2の係数aが正の数なので下に凸、さらにa=1なので幅は狭くもなく広くもなくいきましょう。

まとめ

　二次関数の概形の描き方についてまとめます。

　グラフの概形を描けるようになれば、問題文の状況を正しく、視覚的に理解できるようになります。

　関数の問題が苦手だというあなたでも、グラフの概形を描けるようになれば苦手克服へ大きく前進できますよ。