【高校受験】模試が解けないなら見て！合同の証明問題の解き方を例題で解説

　高校受験生のあなたにとって、合同証明の問題は鬼門でしょう。

　高校入試にはよく出るけど、模試で合同証明の問題をなかなか解けないという人が多いはずです。

　なぜなら、あと一つの合同条件を見つけにくいから。

　この記事では、模試で合同証明の問題を解けない高校受験生に向けて、合同証明を解くポイント『あと一つの合同条件の見つけ方』をお話しします。

　その後で例題を行い、先に解説したポイントを押さえた解説をします。

　そもそも合同条件を覚えていない！　という人は、以下の記事から読んでください。

合同証明は『あと一つの条件』が見つかれば解ける

　合同証明で難しいのは、合同条件を満たす根拠があと一つ見つからないことです。

　ここからはそのことについて少しお話しした後、『あと一つの条件』を見つけるコツを解説します。

合同条件を満たす根拠が『あと一つ』見つからないから難しい

　合同証明で難しいのは、合同条件を満たす根拠があと一つ見つからないことです。

　例えば『二組の辺とその間の角が等しい』が答えの場合、二組の辺が等しいことはパッと見ただけでわかっても、その間の角が等しいといえる根拠が見つからないときがありませんか？

　このように高校入試問題や模試では、合同条件があと一つ見つからないことがあります。

　逆に言えば、『あと一つの条件』さえ見つけられれば、合同証明の問題はそこまで難しくはないのです。

『あと一つの条件』を見つけるコツ

　あと一つの条件を見つけるコツは、あと一つ、どこが等しいと言えれば証明できるかな？　と逆算して考えることです。

　例えば合同を証明したい三角形の二組の辺が等しいことがわかったとしましょう。

　このとき、あと一つ何が等しいとわかれば合同であると言えるでしょうか？

二組の辺の、間の角が等しいと言えればいいね！

残りの辺が等しいことが言えてもいいね！

　このように、あと一つ何が等しいとわかれば合同と証明できるのかを考えてから、等しいと言える根拠を探すのです。

　あと一つ何が等しいとわかれば合同を証明できるかを考える練習も、ぜひやってみてくださいね。

【例題】『あと一つの条件』がなかなか見つからない合同証明

　ここからは『あと一つの条件』がなかなか見つからない合同証明の例題を解いてみましょう。

例題

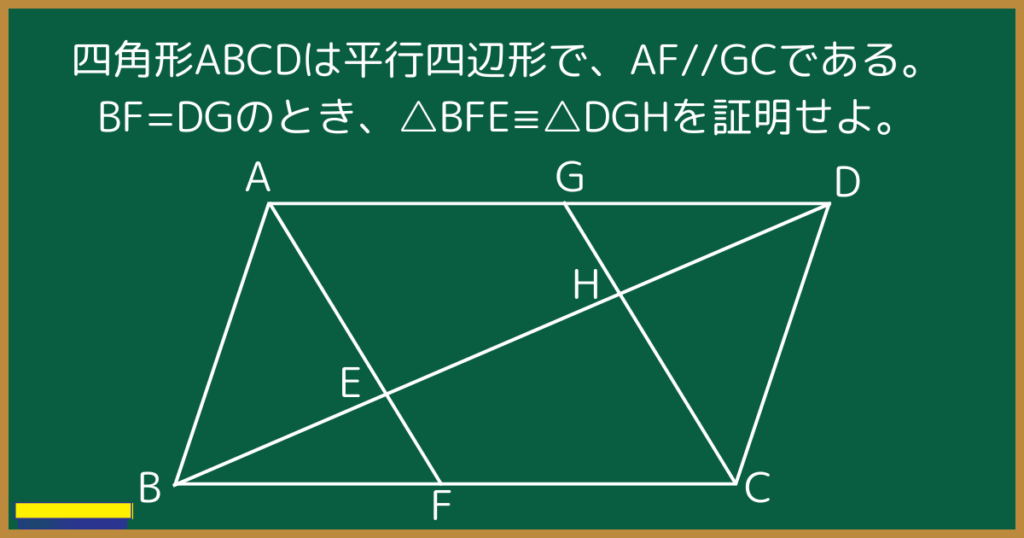
　問題文よりBF＝DG

　また、平行四辺形の向かい合った辺は平行なので、平行線の錯角より∠EBF＝∠HDGであることはパッと見てわかりますね。

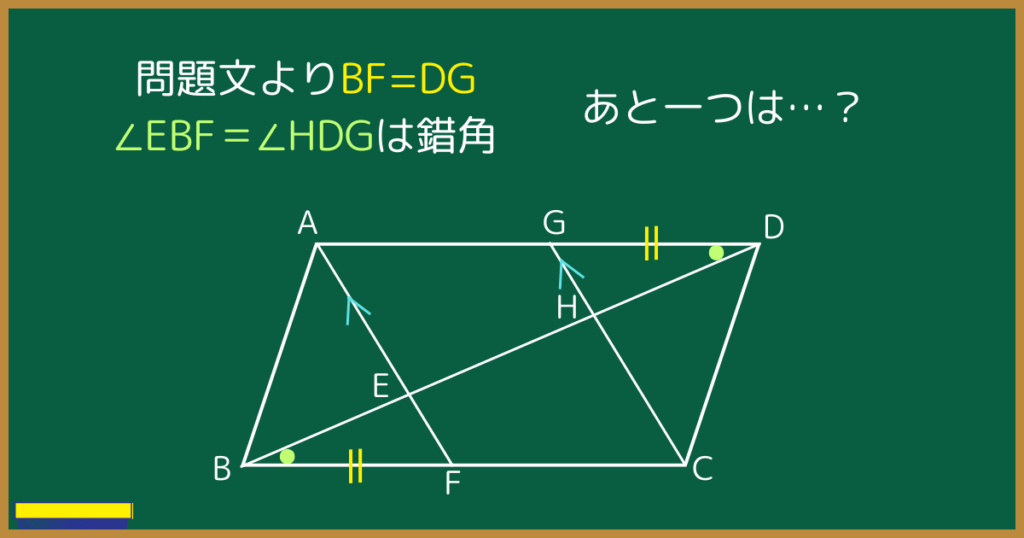
　さて、あと一つの条件が見つけられませんね。

　では、あとは何が等しいと言えれば△BFE≡△DGHを証明できるでしょうか？

∠BFE＝∠DGHが言えれば、『一組の辺とその両端の角が等しい』ことから合同と言えるね。

BE=DHが言えれば、『二組の辺とその間の角が等しい』と言えるね

　この問題では、実は∠BFE＝∠DGHが言えます。

大体こういうときは、角が等しいと言えるパターンが多いです。

もしも辺の長さが等しいと言えるパターンであれば、問題文の見落としが考えられます。

　さて、ここからは∠BFE＝∠DGHである根拠を探しましょう。

　根拠の見つけ方は上でお話した通りです。

　今回は角度∠BFE＝∠DGHが等しいことを言いたいので、錯角や同位角を用いていきましょう。

　まず、平行線の錯角より∠BFE＝∠EAGですね。

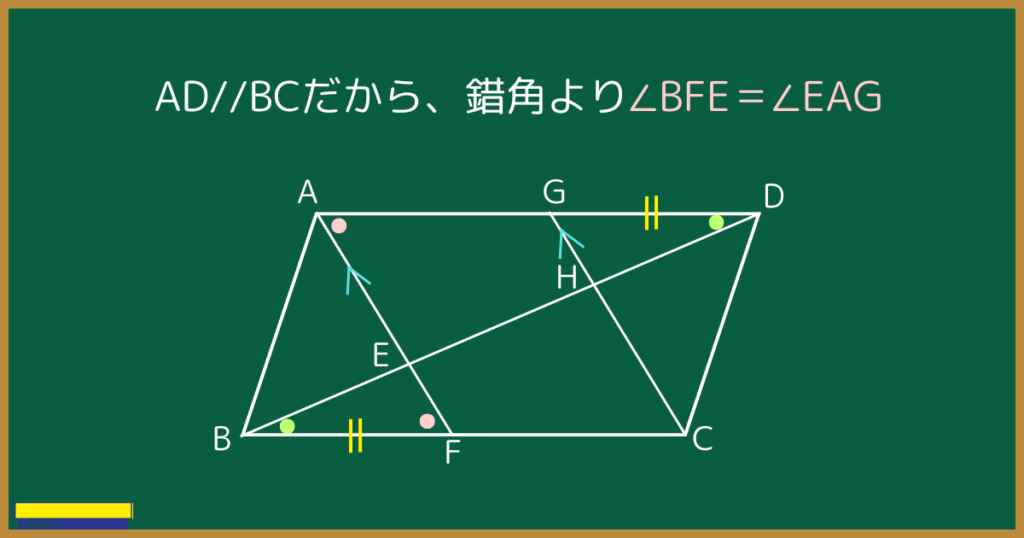
∠BFE＝∠DGHを言いたいのに、

∠BFE＝∠EAGの話？

　次に、∠EAGの同位角を言いましょう。

　問題文よりAF//GCなので、∠EAGの同位角は∠DGH

　つまり∠DGH＝∠EAGですね。

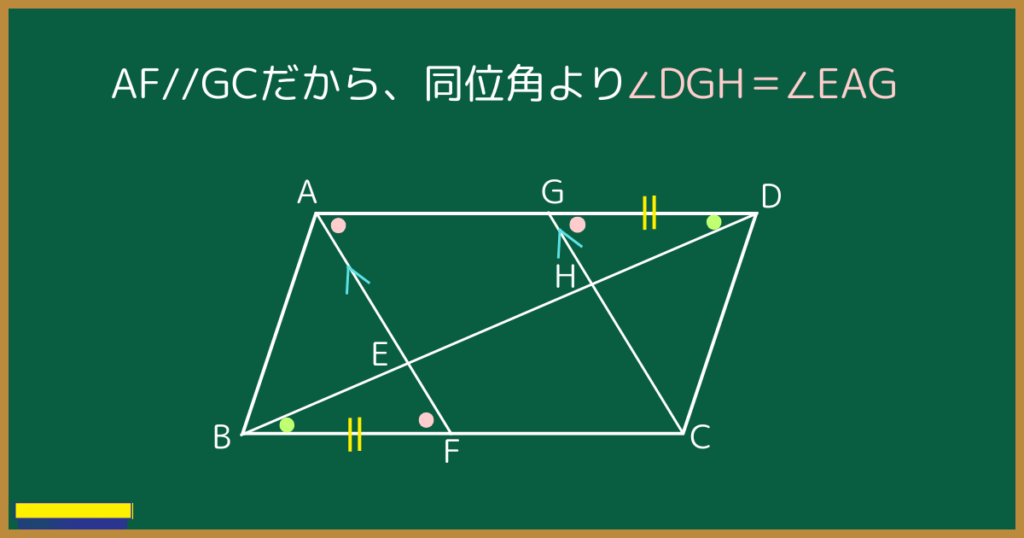
　よって平行線の錯角より∠BFE＝∠EAG

　さらに同位角より∠DGH＝∠EAG

　つまり∠BFE＝∠DGHと言えます。

　このように錯角や同位角を用いて、『あと一つの条件』を見つけるのです。

　以下で解答をまとめます。

解答

　△BFEと△DGHにおいて、

　問題文よりBF＝DG…①

　平行線の錯角より∠EBF＝∠HDG…②

　また、平行線の錯角より∠BFE＝∠EAG…③

　AF//GCなので同位角より∠DGH＝∠EAG…④

　③と④より∠BFE＝∠DGH…⑤

　①、②、⑤より一組の辺とその両端の角がそれぞれ等しいので

　△BFE≡△DGH

まとめ

　図形の証明問題を苦手とする中学生は多くいます。

　しかし合同証明が難しいときの対処法を知っていれば、簡単に問題を解けるようになります。

　この記事で学んだことを活かして、模試や入試を頑張っていきましょう！