【合同・相似】証明問題ができない高校受験生必見！条件を見つけるコツを紹介します

　図形の証明が得意！　という高校受験生はそういないでしょう。

　合同条件や相似条件を覚えても、なかなか実践で得点できない人が多いのではないでしょうか。

　その原因の一つに、合同条件や相似条件を『あと一つ見つけられない』ことがあります。

　等しい辺や角をいくつか見つけられても、合同条件や相似条件に合わず証明ができなかったという経験がありませんか？

　この記事では合同条件や相似条件をあと一つ見つけられない理由とその対策を解説します。

　その後で、合同条件や相似条件をあと一つ見つけられるようになる問題を行っていきます。

図形の証明問題ができない理由とその対策

　図形の証明問題がどうしても解けない原因の一つに、合同条件や相似条件を『あと一つ見つけられない』ことがあります。

　なぜ条件をあと一つ見つけられないのか？

　どうしたら条件を見つけられるようになるのか？

　まずはこの2つを解説します。

合同条件や相似条件を『あと一つ見つけられない』から証明ができない

　図形の証明問題がどうしても解けない原因の一つに、合同条件や相似条件を『あと一つ見つけられない』ことがあります。

　問題を解いているとき、一度はこう思ったことがあるでしょう。

条件に合わない……

　ここの直線の長さが同じ。

　あそこの角度が同じ。

　いろいろと合同条件や相似条件になりそうな要素は見つかるけれど、例えば『三組の辺がそれぞれ等しい』とか『二組の辺とその間の角がそれぞれ等しい』とかいう合同条件や相似条件に当てはまらない。

　そんなことがあるはずです。

図形の証明問題の条件『あと一つ』を見つけられない理由

　図形の証明問題の条件『あと一つ』を見つけられない理由は、あと一つの条件はパッと見ではわからないからです。

　他の条件がすぐ見つかるのは、『AB=CDである』とか『∠ABC＝∠DEFである』などどあらかじめ問題文中に書いてあるから。

　また、錯角や平行四辺形の対辺・対角など、パッと見でわかりやすいからです。

　しかしあと一つの条件は、錯角や同位角、平行四辺形や二等辺三角形などの性質を駆使して、自分で見つけないといけないことが多いのです。

　例として以下の問題を見ていきましょう。

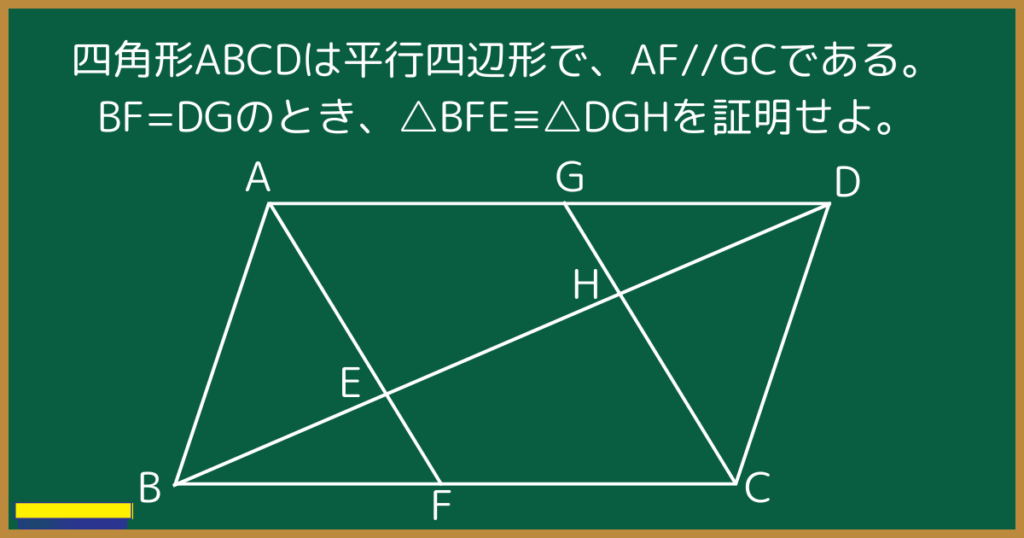
　この問題を見て、問題文よりBF=DG、平行線の錯角より∠EBF＝∠HDGであることはパッとわかるでしょう。

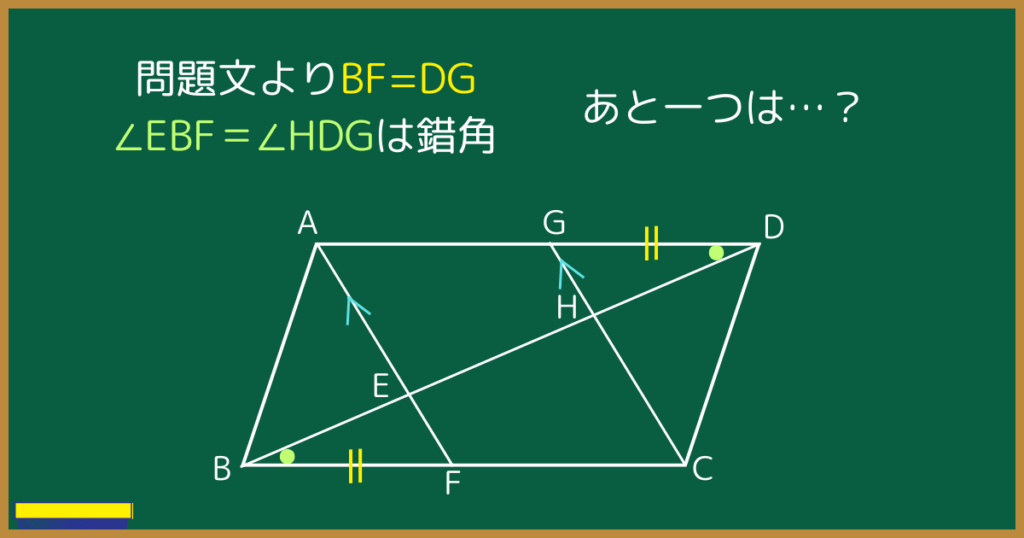
　でも、パッとわかる条件だけでは合同を証明できませんよね。

　実はこの問題、錯角と対頂角を駆使してあるもう一つの角が等しいことを言わなければならないのです。

　そこが難しいために、証明が解けないということになるのです。

『あと一つ』の条件を見つけられるようになるには？

　パッと見ただけでわからない条件を見つけるのは、なかなか骨が折れます。

　そこで、あと一つ、どこが等しいと言えれば証明できるかな？　と逆算して考えるのです。

　では、上の合同証明の問題は、あと一つどこの辺や角が等しければ合同条件がそろうと思いますか？

DG＝BFなら、2組の辺とその間の角が等しくなるね

∠DHG＝∠BEFなら、1組の辺とその両端の角が等しいと言える！

　このように、どこの辺や角が等しければ合同条件・相似条件がそろうかを考えます。

　その後で、その辺や角が等しくなる理由を探すのです。

　なんの当てもなく等しい辺や角を探そうとするよりは遥かにラクですよ。

図形の証明問題の条件『あと一つ』を見つけられるようになる問題

　ここまでで、図形の証明ができない原因の一つに、あと一つの合同条件または相似条件を見つけられないことをあげました。

　あと一つの条件を探すためには、どこの辺や角が等しければ良いかを考えてから、辺や角が等しい理由を考えましょうとお話しました。

　ここからは、あと一つ何が等しければ合同または相似であると言えるかを考える問題を行いましょう。

　この問題を行うことで、

三角形の合同編

問題

次の2つの三角形は、あと一つ何が等しいといえれば合同であるといえるか答えなさい。

また、その時の合同条件も答えなさい。

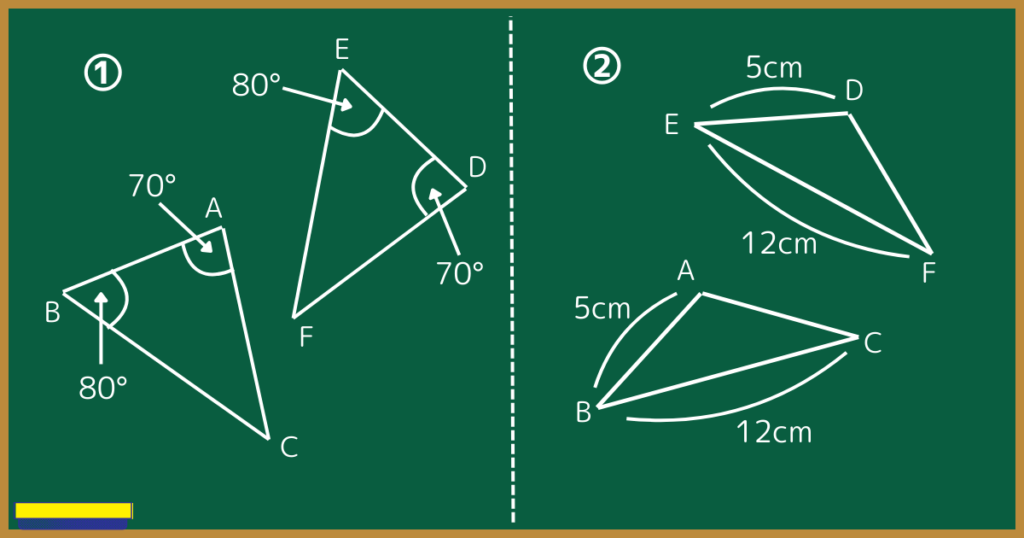
　①について。

　角度が2つわかっているので、あとはAB＝DEが言えれば、『一組の辺とその両端の角が等しい』と言えます。

　②について。

　2組の辺が等しいとわかっているので、∠B＝∠Dと言えれば『二組の辺とその間の角が等しい』と言えます。

　また、AC＝DFが言えれば『三組の辺がそれぞれ等しい』と言えますね。

相似編

問題

次の2つの三角形は、あと一つ何が等しいといえれば相似であるといえるか答えなさい。

また、その時の相似条件も答えなさい。

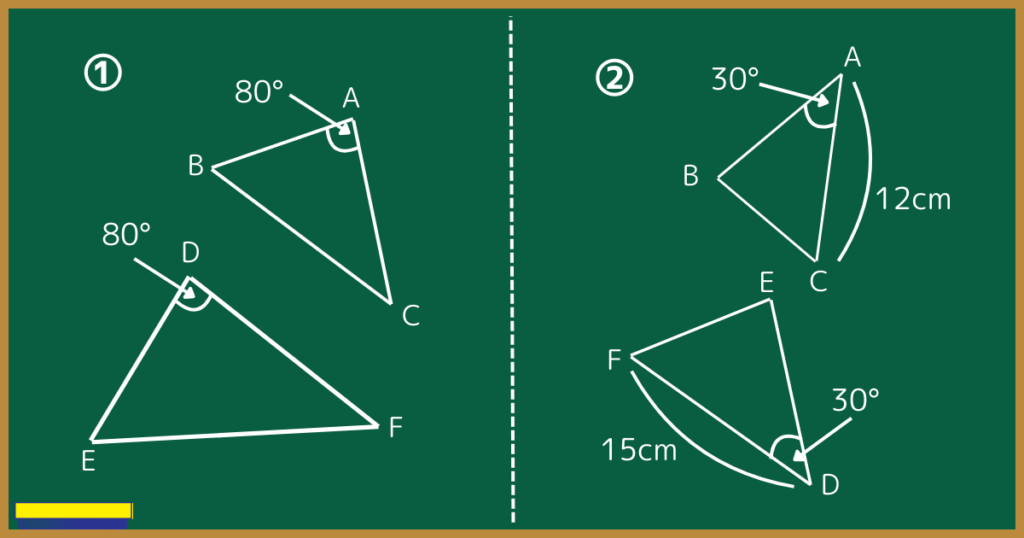
　①について。

　角度が1つわかっているので、あとは∠B＝∠Eまたは∠C＝∠Fがいえれば、『2組の角が等しい』といえます。

　②について。

　角度が1つと、辺が1組わかっています。

　辺の比はAC：DF＝12：15＝4：5ですね。

　つまり、BC：EF＝4：5であるとわかれば『2組の辺の比とその間の角』が等しいと言えます。

まとめ

　多くの高校受験生は、証明問題を苦手としています。

　だからこそ、あなただけはぜひ証明問題を解けるようにしてほしいのです。

　ライバルに差を付けて、志望校合格を目指しましょう！