【中3数学】円周角の定理の逆とは何か?基礎から解説【同じ側とは？】

　円周角の定理の逆について、教科書を読んでもよくわからなかったという人がいることでしょう。

　そもそも円周角の定理とはなんなのかを、あなたは説明できますか？

　円周角の定理がなんなのかを説明できなければ、その逆と言われてもピンとこないのは当然です。

　この記事では円周角の定理の逆とは何かを解説します。

　前提知識である円周角の定理から確認しているので、知識に不安がある人でも安心して読んでくださいね。

　また、円周角の定理の逆でよく出てくる『同じ側』という説明が何を意味するのかも解説しています。

【前提知識】円周角の定理とは？

　円周角の定理の『逆』を学習する前に、まず円周角の定理とは何かを説明できますか？

　円周角の定理では、下図のように円周上の4点を結ぶと円周角が等しくなることを言います。

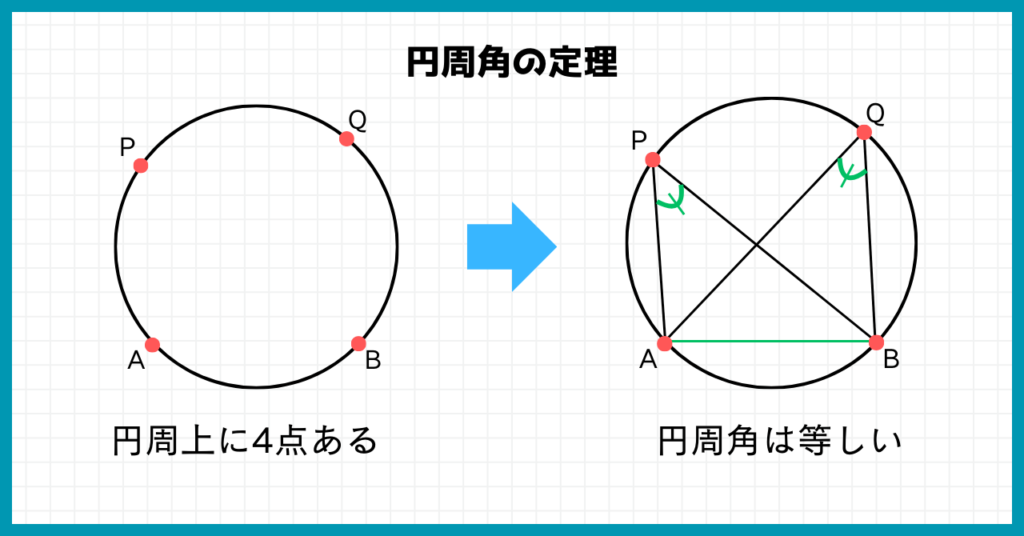
　つまり円周角の定理とは『4点が円周上にある⇒円周角が等しくなる』ことを言っているのです。

　ここからは円周角の定理の逆について解説します。

　また、『円周角の定理の逆』の説明でよく出てくる『同じ側』とはどういう意味かも解説します。

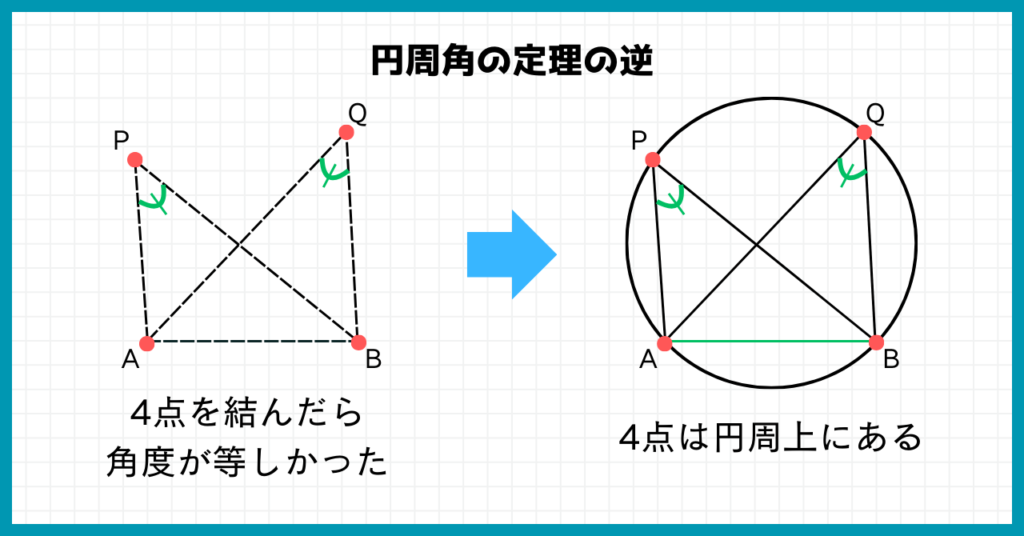
　円周角の定理の逆とは、文字通り『円周角の定理』の『逆』を言っているに過ぎません。

　円周角の定理とは『4点が円周上にある⇒円周角が等しくなる』ことを言っているのでしたね。

　『円周角の定理の逆』とはつまり、『4点を結んだら角度(円周角)が等しい⇒4点が円周上にある』ことを言っているのです。

　円周角の定理の逆について教科書で調べてみたら、『同じ側』というワードがよく出てくるかと思います。

　『同じ側』とは下の図でいうと、直線ABに対して点Pと点Qの2点が弧の同じ側にあるということなのです。

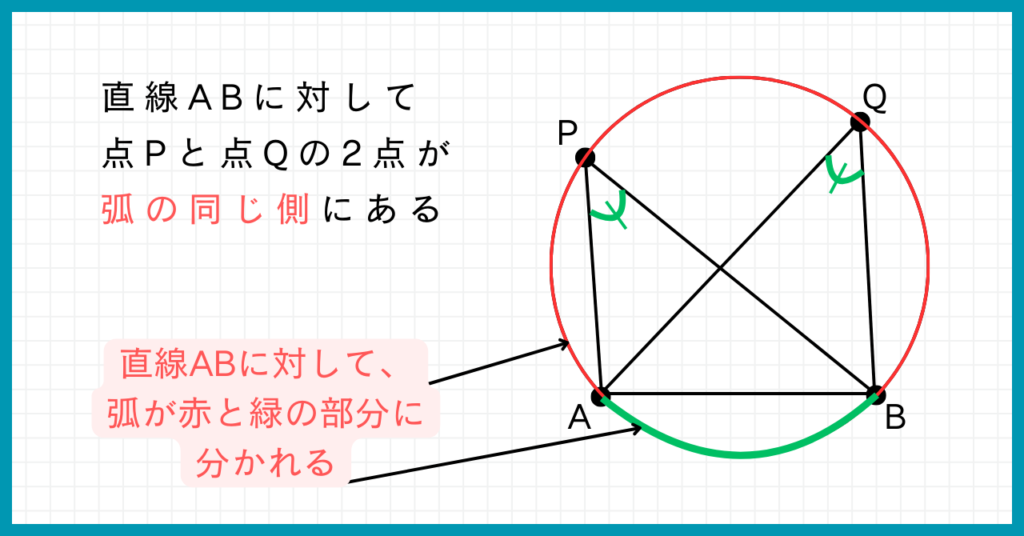
　直線ABは、弧を2つに分けていますよね。

　点Pと点Qが2つとも同じ側の弧にないと、円周角の定理の逆が成り立たないのです。

　ちなみに、直線ABに対して点Pと点Qがそれぞれ弧の逆側にある場合は以下の図のようになります。

　円周角の定理の逆を理解するには、説明を図で正しく表す必要があります。

　あまり登場頻度は高くないので、円周角の定理とは何かを忘れがちです。

　しばらくしたらまた復習しましょう。