【相似】平行線と比の公式は丸暗記不要!今すぐ理解できる解説をします

平行線と比の公式は、AB:AD=AC:AEなど、パッと見ただけではわかりにくいですよね。
さらに図と照らし合わせて覚えなければいけないので、理解するのに苦労することでしょう。
しかし平行線と比の公式は、2つの三角形が相似であることがわかれば、苦労して暗記するまでもなく理解し問題を解けるようになるのです。
この記事では平行線と比の公式について、丸暗記せずに理解できるよう解説します。
この記事を読めば、複雑に見える公式でもスッキリ理解できますよ。
【ポイント】2つの三角形は相似である
平行線と比の公式を理解するポイントは、下の図でBC//DEのとき△ABC∽△ADEであることです。
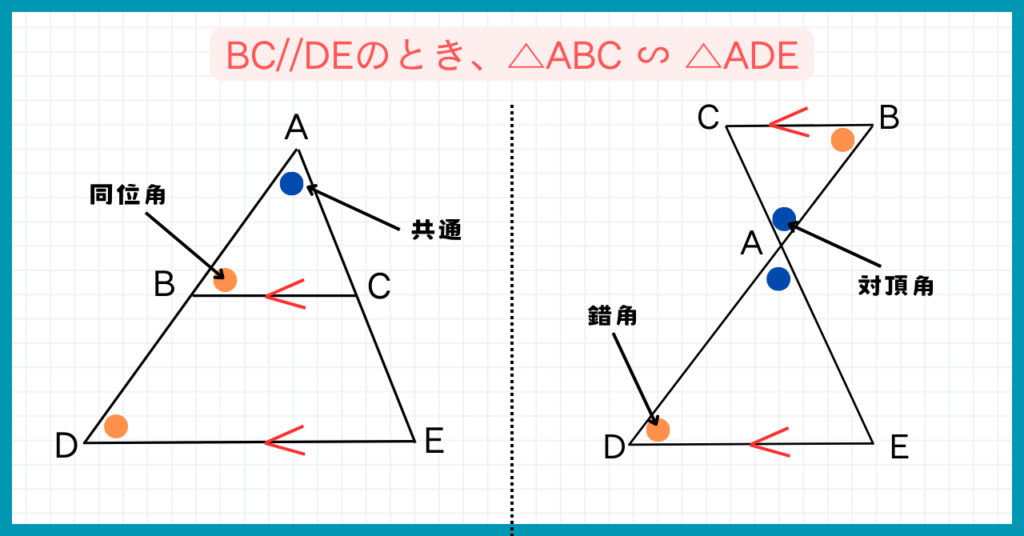

△ABCと△ADEが相似なことと公式がどう関係するの?
相似な図形であれば、対応する辺の比が等しいことは覚えていますか?
実は平行線と比の公式は、相似な図形の対応する辺の比が等しいことを言っているに過ぎないのです。
平行線と比の公式
ここまでで、平行線と比の公式に出てくる2つの三角形は相似であることをお話しましたね。
実は平行線と比の公式は、2つの相似な三角形の対応する辺の比が等しいことを言っているに過ぎません。
以下で公式を詳しく解説します。
【基本】AB:AD=AC:AE
平行線と比の公式で、まずは基本を確認しましょう。
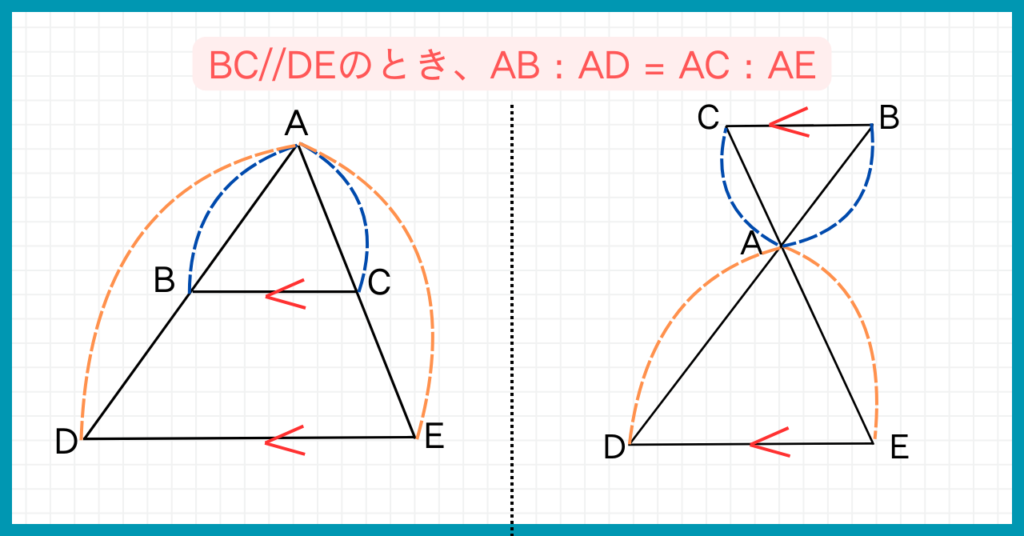
これは△ABCと△ADEが相似であることがわかっていれば、簡単に理解できるはずです。
相似な図形は対応する辺の比が等しいので、上の図でAB:AD=AC:AEが成り立ちます。
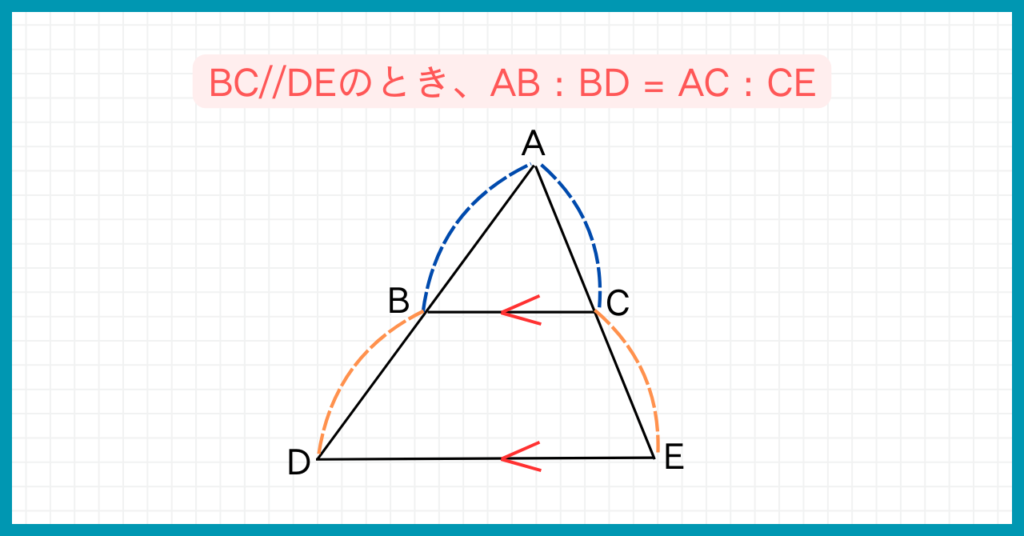
【基本からの派生】AB:BD=AC:CE
次に基本から派生した公式を見ていきましょう。

BDとCEって、三角形の辺じゃないよね?
これまでで、平行線と比の公式は2つの三角形が相似であることから来ているとお話してきました。
ゆえに、三角形の辺ではないBDやCEが出てきて戸惑っている人がいるかもしれません。
しかしこの公式は、平行線と比の公式①が基本となって成り立っています。
平行線と比の公式①より、△ABC∽△ADEなのでAB:AD=AC:AEが成り立つのでした。
ここで、△ABC∽△ADE=1:3としましょう。
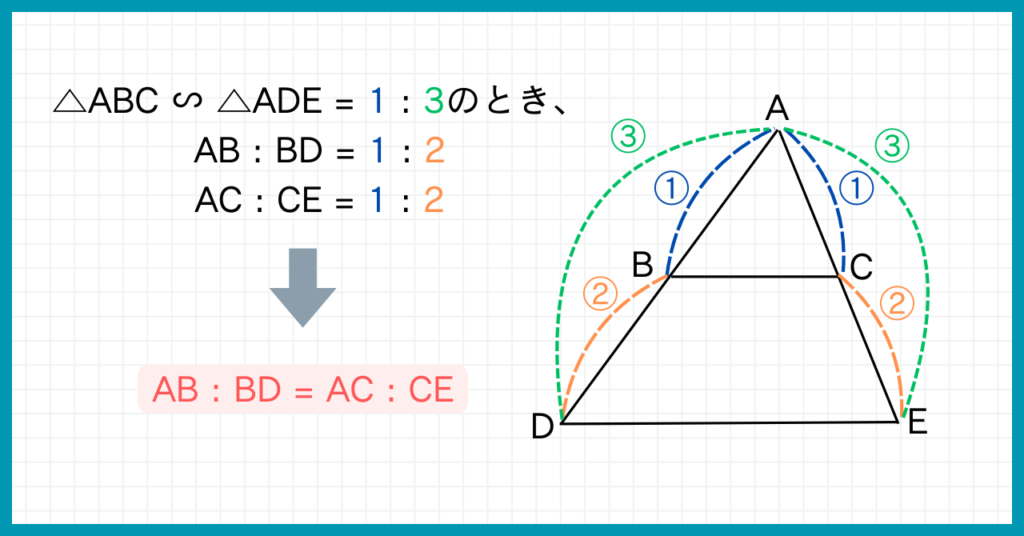
上の図のように、AB:AD=1:2になります。
また、AC:AE=1:2になりますよね。
このようにAB:ADとAC:AEが等しくなります。
よって、BC//DEのとき△ABC∽△ADEであり、このときAB:AD=AC:AEが成り立つのです。
まとめ
平行線と比の公式は、当たり前のことを言っているに過ぎません。
相似な図形の性質を理解していれば、特に苦労することなく覚えられますよ。
あとは学校の問題集などを用いて問題演習を行い、テストで得点源にしましょう!

コメントを残す