【中2数学】平行線と角の応用『星形』の内角の和が180°になる理由を解説

　星形の内角の和は180°だと習っても、なぜそうなるのかわからず困っている人は多いことでしょう。

　この記事では、平行線と角の応用『星形』の内角の和が、なぜ180°になるのかを解説します。

　決して難しくはありません。なぜなら、星形の前に習った『ブーメラン』の性質を覚えていればすぐに理解できるからです。

　『ブーメラン』の性質を忘れてしまった人のために、ブーメランの性質の説明もしているので、安心して読んでくださいね。

平行線と角『星形』

　『星形』の内角の和が180°になる理由を解説する前に、以下の前提知識を確認しましょう。

　前提知識は大丈夫！　という人は『星形の内角の和が180°になる理由』だけを読んでください。

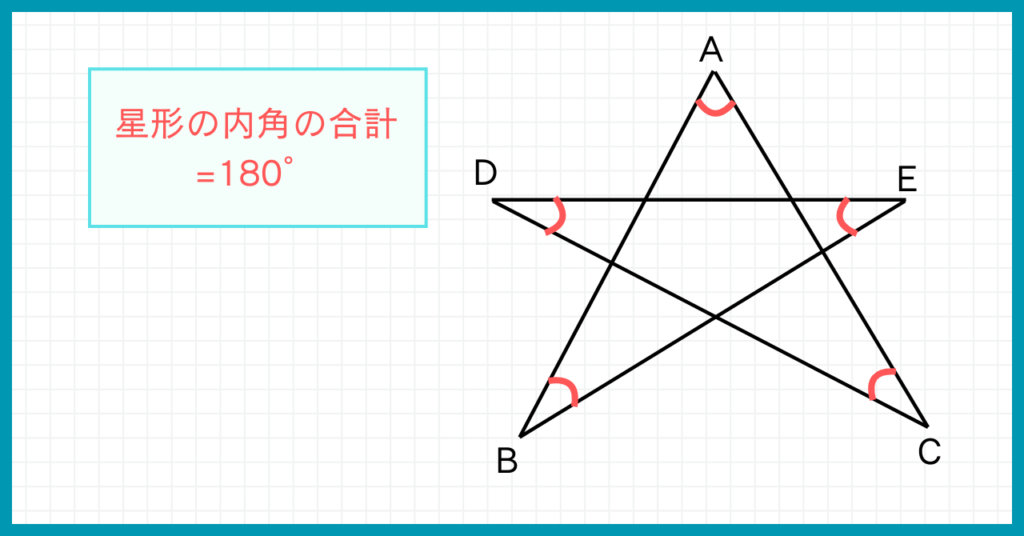
　上の図のように、星形の尖った部分の角度を全て足したら180°になります。

　星形の内角の和が180°になる理由を理解するには、星形の前に習った『ブーメラン』の性質を覚えている必要があります。

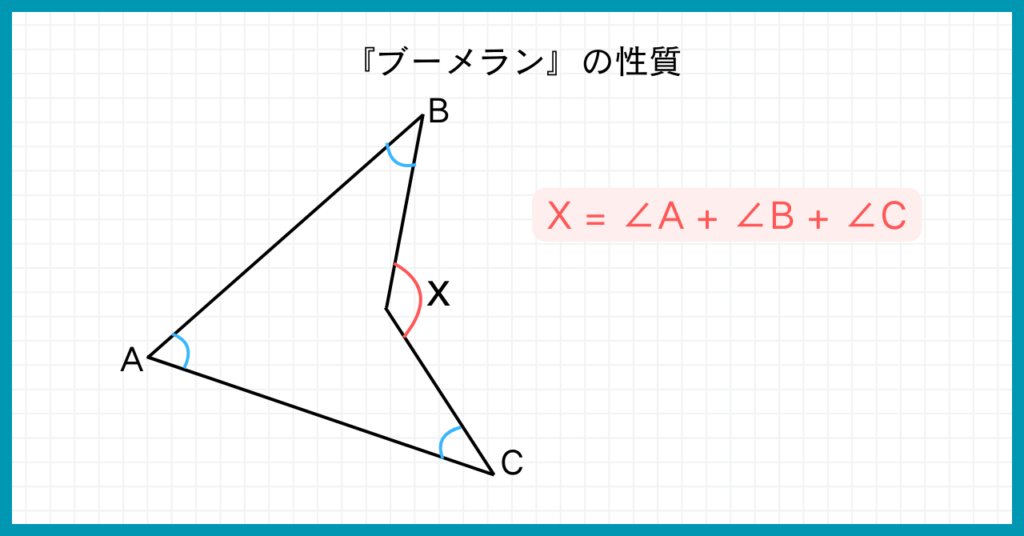
　上の図のように、ブーメランの内角の和はへこみの部分の角度と等しくなります。

　ブーメランについて忘れてしまった！　という人は以下の記事も読んでみてください。

【中2数学】平行線と角の応用『ブーメラン』の解き方を解説

　ここからは『星形』の内角の和が180°になる理由を解説します。

　ポイントは以下の2つです。

　まずは星形を、ブーメランと三角形に分けましょう。

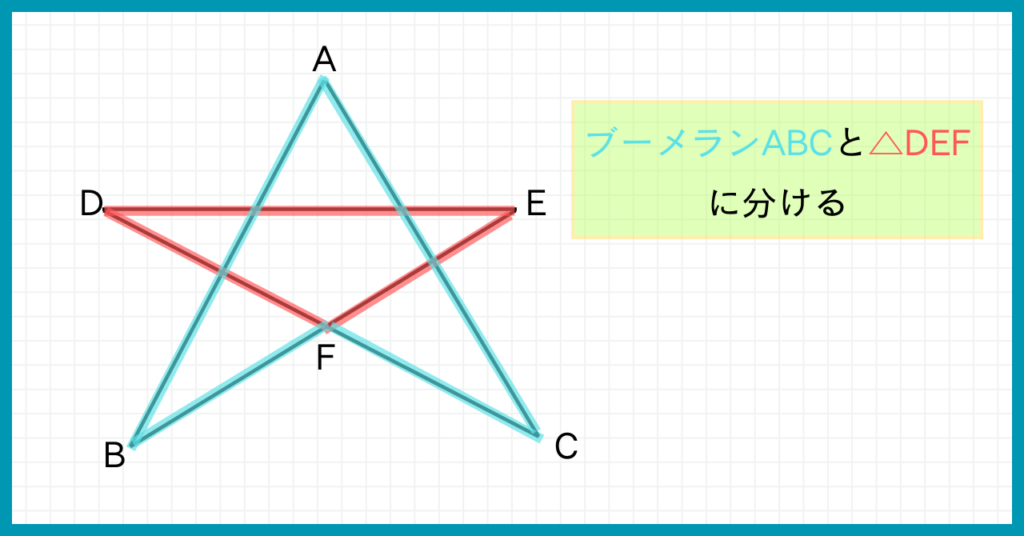
　ブーメランの方を見てみましょう。

　ブーメランの内角の和は、へこみの部分の角度と等しくなるのでしたね。

　さらに対頂角なので、へこみの部分∠BFC=∠DFEです。

　次に△DEFを見てみましょう。

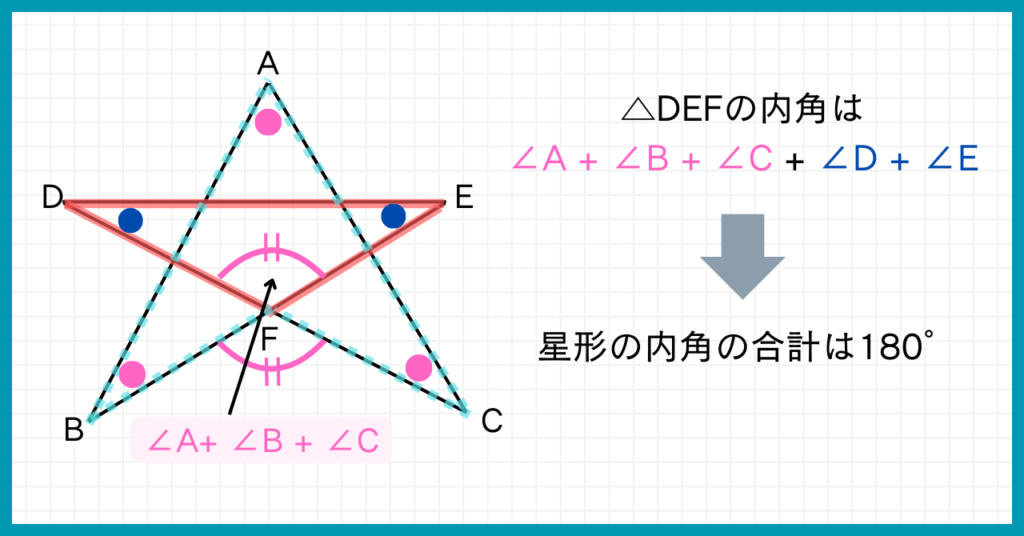
　△DEFにおいて∠DFE=∠A+∠B+∠Cです。

　△DEFの内角には、∠DEFに加えて∠Dと∠Eがあります。

　つまり△DEFの内角は、∠A+∠B+∠C+∠D+∠Eでできているのです。

　三角形の内角の和は180°でしたね。

　よって、∠A+∠B+∠C+∠D+∠E＝180°というわけです。

　平行線と角の応用『星形』は、ブーメラン形の性質や三角形の内角の和といった既習の内容を用いれば理解できましたね。

　星形だけでなく、応用問題を難しそうだと敬遠せずに基礎知識を駆使して新しい内容を理解していきましょう。