【全パターン共通】一次関数の式を求めるたった1つの考え方とその解き方を解説

一次関数の式を求める問いには様々なパターンがあります。
中学生のあなたは、どのパターンでどの解き方をすれば良いか迷ってしまうことでしょう。
しかし、一次関数の式を求める問いには全パターンで共通するたった1つの考え方があります。
この記事では、一次関数の式を求める問い全てに共通するたった1つの考え方を解説します。
この記事を読めば、一次関数の式を求める問いの本質がわかり、どんなパターンが出題されても迷うことなく解答できるようになりますよ!
【全パターン共通】一次関数の式を求めるたった1つの考え方
一次関数の式は$\color{red}{y=ax+b}$で表されますよね。
つまり一次関数の式を求めるには、$\color{red}{y=ax+b}$のaとbを求めればよいのです。
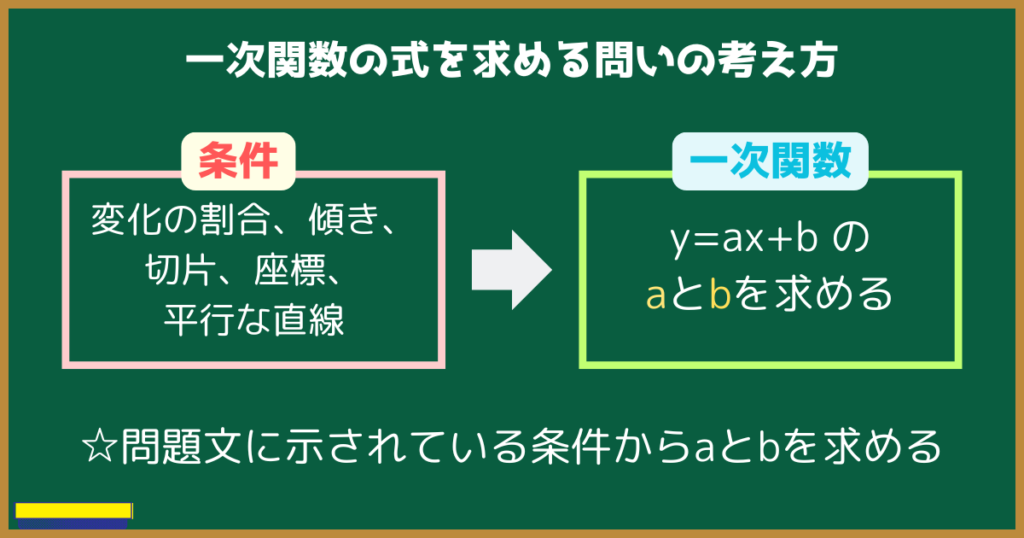
問題文中には様々な条件が示されます。
その条件を駆使して、一次関数のaとbを求めれば問題が解けるのです。
aとbを求めればいいんだ! と考えれば、解き方を覚えなくてもなんとか解けるものですよ。
【4パターン】変化の割合/傾き/切片/平行な直線+座標を与えられたときの解き方
まずは以下4パターンの解き方を解説します。
- 切片+座標
- 変化の割合+座標
- 傾き+座標
- ある一次関数と平行+座標
これらは条件を読んだだけで一次関数$y=ax+b$のaまたはbが分かる問いです。
aまたはbを$y=ax+b$に代入したあと、さらに座標をx,yに代入して一次方程式を解きます。
①切片+座標
まずは切片と座標が示されているパターンです。
例題
以下の条件の一次方程式を求めましょう。
切片が5で、座標(-1,2)を通る。
まず切片が5と言われているので、$y=ax+b$の$b=5$であることがわかります。
よって$y=ax+5$です。
さらに座標(-1,2)を通ることから、$y=ax+5$にx=-1,y=2を代入すればaも求められます。
$y=ax+5$
$2=-a+5$
$a=3$
よってa=3,b=5なので、答えは$y=3x+5$
②変化の割合+座標
例題
以下の条件の一次方程式を求めましょう。
変化の割合が-2で、座標(10,-6)を通る。
変化の割合とは$y=ax+b$のaのことなので、$y=ax+b$に$a=-2$を代入できます。
また座標(10,-6)を通ることから、x=10,y=-6を代入できるので、bを一次方程式で求められます。
$y=-2x+b$
$-6=-2×10+b$
$b=14$
よってa=-2,b=14なので、答えは$y=-2x+14$
③傾き+座標
例題
以下の条件の一次方程式を求めましょう。
傾きが5で、座標(3,8)を通る。
傾きが5ということは、$y=ax+b$に$a=5$を代入できます。
また座標(3,8)を通ることから、x=3,y=8を代入できるので、bを一次方程式で求められます。
$y=5x+b$
$8=5×3+b$
$b=-7$
よってa=5,b=-7なので、答えは$y=5x-7$
④平行な直線+座標
例題
以下の条件の一次方程式を求めましょう。
直線$y=6x+5$に平行で、座標(2,11)を通る。
直線$y=6x+5$に平行とはどういうことでしょうか。
求める一次関数が直線y=6x+5と平行ということは、求める一次関数の傾きは直線y=6x+5と同じということです。
つまり$a=6$として一次関数を求めます。
あとは③傾き+座標の解き方と同じです。
a=6,b=-1となり、答えは$y=6x-1$
【2パターン】座標2点を与えられたときの解き方
次に座標を2点与えられた時の一次関数の式を求める問いについて、2パターン解説します。
- (k,l)と(m,n)が与えられる
- (k,l)と(m,0)が与えられる
①は0を含まない座標、②は0を含む座標が与えられます。
①と②は同じ解き方でも問題なく解けますが、②の$(m,0)$が切片であることを用いれば簡単に解けます。
①(k,l)と(m,n)が与えられる
例題
以下の条件の一次方程式を求めましょう。
A(3,-4)とB(-1,12)を通る。
解き方は2つあります。
- 変化の割合を求めてから一次方程式を作る
- 連立方程式を作る
まずは①変化の割合を求めてから一次方程式を作る方法を解説します。
変化の割合とは、ある関数での、xの増加量1あたりのyの増加量のことでした。
つまり、yの増加量をxの増加量で割ればよいのでしたね。
座標Bから座標Aのxの増加量は3-(-1)=4
またyの増加量は-4-12=-16
よって変化の割合は$\color{red}{\frac{-16}{4}=-4}$
つまりa=-4であることがわかりました。
$y=ax+b$に$a=-4$を代入します。
さらにA(3,-4)を通ることからx=3,y=-4を代入すればbも求められますね。
$y=-4x+b$
$-4=-4×3+b$
$b=8$
よってa=-4,b=8となり、答えはy=-4x+8
次に②連立方程式を作る方法を解説します。
一次関数の式$y=ax+b$に座標を代入し、a,bを求めます。
座標は2つあるので式は2通りでき、連立方程式を立てられるのです。
A(3,-4)を通ることより、x=3,y=-4を$y=ax+b$に代入します。
$-4=3a-b$…①
また、B(-1,12)を通ることより、x=-1,y=12を$y=ax+b$に代入します。
$12=-a+b$…②
式①と②を連立することで、a,bを求めます。
\[
\left\{
\begin{array}{l}
-4=3a-b・・・① \\
12=-a+b・・・②
\end{array}
\right.
\]
これを解くとa=-4,b=8となり、答えはy=-4x+8

どちらの方法で解いても当然答えは同じになるから、
好きな方で解こうね!
②(k,l)と(m,0)が与えられる
例題
以下の条件の一次方程式を求めましょう。
A(5,37)とB(0,2)を通る。

(k,l)と(m,n)が与えられる問題と何が違うの?
一見すると2つの座標を与えられるタイプの問題です。
しかし、座標Bについて何か気づきませんか?

座標B(0,2)を通るということは、求める一次関数の切片が(0,2)ということ。
つまりb=2です。
この問いでは切片bが分かったので、あとは切片と座標が条件として示されているパターンと同じ解き方です。
$y=ax+2$に座標A(5,37)を代入します。
$37=a×5+2$
a=7
よってa=7,b=2となり、答えはy=7x+2
まとめ
一次関数の式の求め方についてまとめます。
一次方程式の式を求める問題は様々なパターンがありますが、全て同じ考え方で解けます。
あなたは各パターンの解き方をそれぞれ覚えるのではなく、解き方の本質『一次関数のa,bを求めることを考える』を理解しましたね。
あなたはきっと、テストでも迷うことなく解答できるでしょう。

コメントを残す