【連立方程式の利用】池の周りを歩く問題の考え方と解き方を解説【図解】

　連立方程式の利用で難しいのは、文章を読み取り自分で式を立てることですよね。

　連立方程式の利用『池の周りを歩く問い』では、特に2人の歩いた距離を引いて池の周りの距離との方程式を作る時に想像力が必要になります。

　この記事では連立方程式の利用『池の周りを歩く問い』の考え方を解説します。

　例題の解説だけでなく、どうやって式を立てるのか、またなぜそのような式が立つのかの理由を解説しています。

【連立方程式の利用】池の周りを歩く問いの考え方

　まずは池の周りを歩く問いの考え方を一言で簡潔に解説します。

　その後で、連立方程式の立て方とその式が立つ理由を、図を用いて解説します。

池の周りを歩く問いの考え方を一言で言うと？

　池の周りを歩く問いの考え方を一言で言うと以下のようになります。

　例えば、(Aさんが歩いた距離)+(Bさんが歩いた距離)＝(池の周りの長さ)のような式を立てます。

　歩いた距離を計算で出すにはどうすればいいか。そう、速さの公式を用いるのです。

　速さの求め方を忘れてしまった人は、始めに復習しておきましょう。

【図解】池の周りを歩く問いでの連立方程式の立て方

　池の周りを歩く問いでは、歩く速さの違う2人が以下のような行動をとります。

　池の周りを歩く問いでは、上に挙げた2人の行動を元に方程式を作ります。

　一つずつ詳しく解説します。

　①反対方向に歩き出し、後に出会う

　池の周りを2人が反対方向に向かって歩いたらどうなるでしょうか。

しばらくしたら2人が出会う！

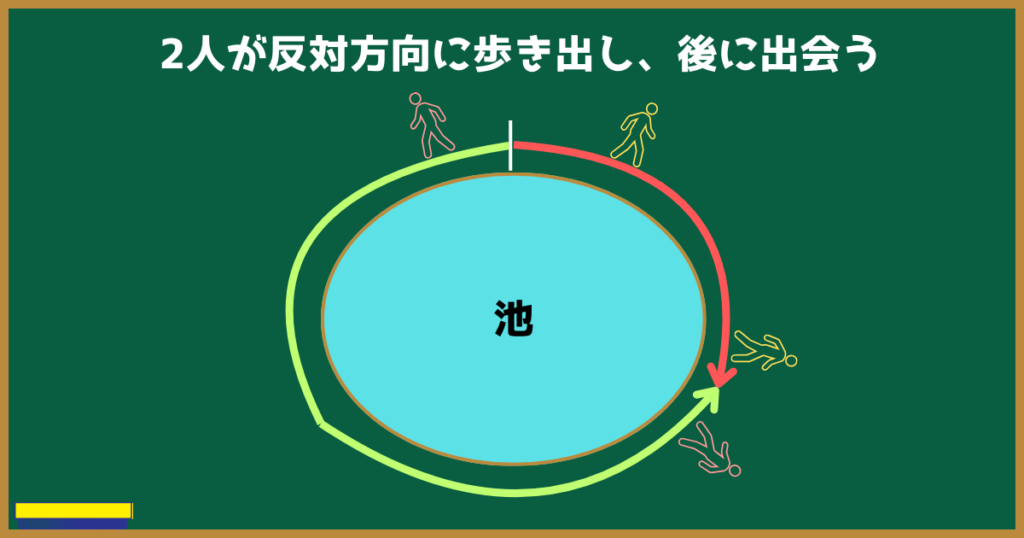
　さて、2人の歩いた距離と池の周りの長さの関係はなんでしょうか？

2人が同じ場所から反対側に歩いて行くから、

2人の歩いた距離の合計と池の周りの長さは等しくなるね！

　つまり、反対方向に歩き出し、後に出会うことから、以下のような方程式を作ります。

　②同じ方向に歩き出し、速く歩く方が遅く歩く方に追いつく

　これはよくイメージしましょう。

　歩く速さの違う2人が、同じ場所から同じ方向に向かって池の周りを歩くとどうなるでしょうか？

歩くのが速い方が追い抜くよね

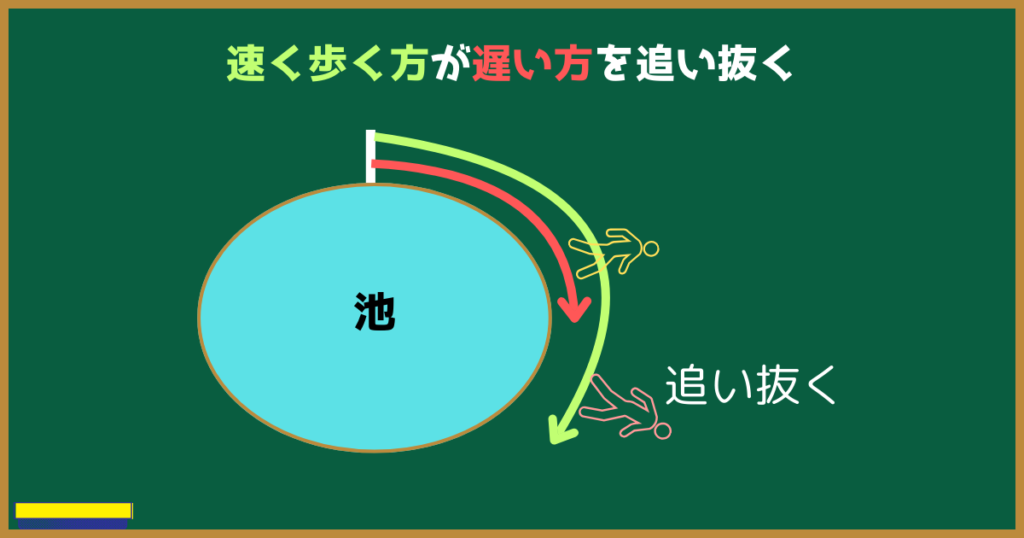
　そのまま歩き続けるとどうなる？

　ヒント、池は丸い。

歩くのが速いほうが、遅い方に追いつく？

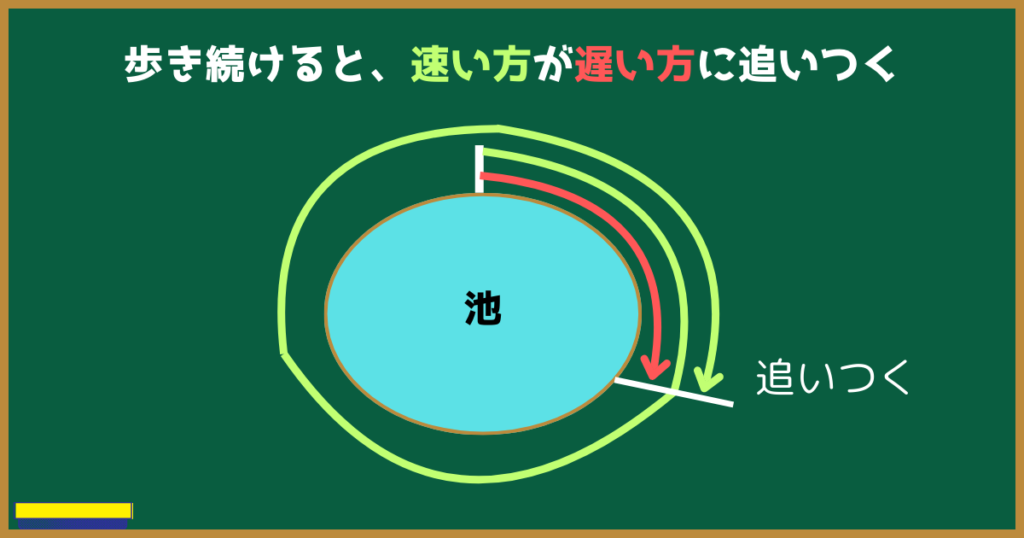
　この速いほうが遅い方に追いついた時に、池の周りとの方程式を作ります。

　ここで、速い方の歩いた距離を見てみましょう。

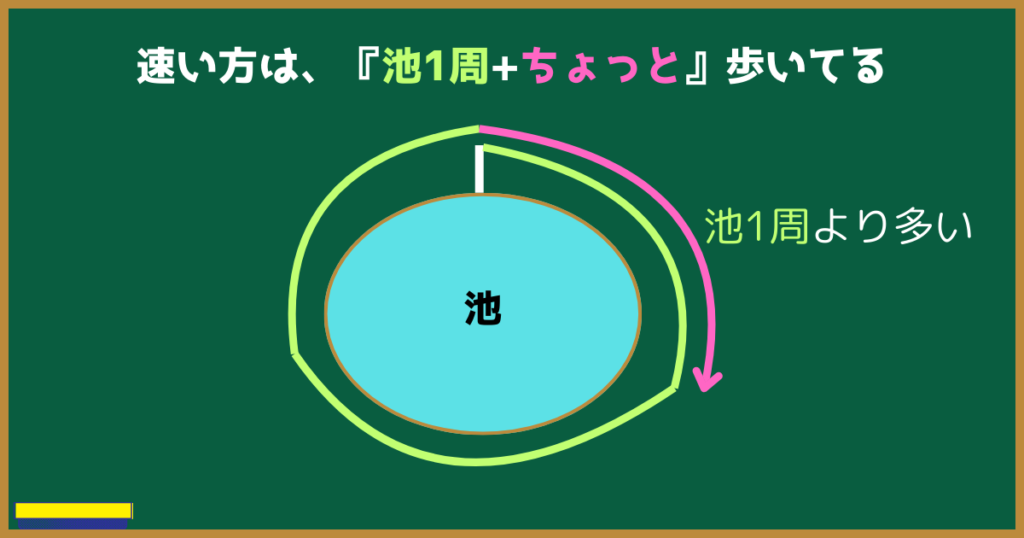
じゃあ、

(速い方が歩いた全部の距離)-(池1周よりも余計に歩いた距離)をすれば、

池1周分の長さになるね。

でも『池1周よりも余計に歩いた距離』って、どうやてわかるんだろう？

　では、池1周よりもちょっと歩いた分の、『ちょっと』とは何か。

　速い方の人は、遅い方の人が歩いた分だけ多く歩いているのです。

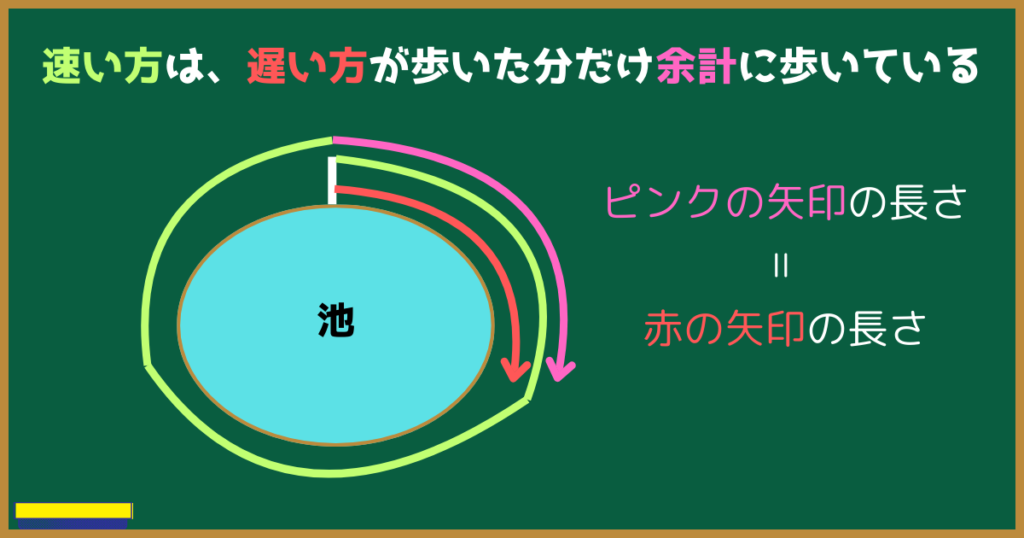
　つまり、以下のような方程式ができます。

【例題で解説】池の周りを歩く問いの解き方

　ここからは具体的な例題を用いて解説します。

　兄と弟の歩く速さを問われているので、兄の歩く速さを$x(m/分)$、弟の歩く速さを$y(m/分)$とします。

　次に式を立てていきます。

　①兄と弟が同時に反対方向に一定の速さで歩いたとき、出発から15分後に出会った

　2人は反対方向に歩いているので、15分後に2人が出会うまでに歩いた距離の合計が池1周分の距離と等しくなります。

　兄の歩く速さが$xm/分$、歩いた時間は15分なので、兄の歩いた距離は$15x(m)$です。

　また弟の歩く速さが$ym/分$、歩いた時間は15分なので、弟の歩いた距離は$15y(m)$です。

　2人の歩いた距離の合計が池1周分の距離に等しくなるので、以下の方程式ができます。

　$\color{red}{15x+15y=3600}$

　②兄弟が最初と同じ速さで、同じ場所から同時に同じ方向へ歩いたとき、3時間後に兄が初めて弟に追いついた。

　この情報から、歩くのが速いのはどっちでしょう？

池は丸いから、同じ場所から同じ方向に歩いたら、速い方が遅い方に追いつくよね。

ということは速い方は兄だ！

　つまり、兄が歩いた距離から弟が歩いた距離を引けば、池1周分の長さと同じになります。

　では、この時に兄と弟が歩いた距離は何mでしょうか？

2人は出発から3時間後に出会ってるから、

×兄が歩いた距離は3x(m)

×弟が歩いた距離は3y(m)

　こう考えた人、それは間違いです。

　兄の歩く速さを$x(m/分)$、弟の歩く速さを$y(m/分)$としましたよね。

　これは分速なので、時間とかけてはいけません。

じゃあ、3時間=180分として、

2人は出発から180分後に出会ってるから、

兄が歩いた距離は180x(m)

弟が歩いた距離は180y(m)

　このことから以下のような方程式ができます。

　$\color{red}{180x-180y=3600}$

　この話がピンと来ない人は、もう一度『連立方程式の立て方』を読んでください。

　以上より、連立方程式ができます。

\[
\left\{
\begin{array}{l}
15x+15y=3600 \\
180x-180y=3600
\end{array}
\right.
\]

上の式と下の式で$x$か$y$を消去して……

あれ？15と180の最小公倍数ってなんだ？

　このままでは計算しづらいので、まずは2つの式を簡単にしましょう。

　$15x+15y=3600$

　両辺を15で割ると、

　$x+y=240$

　また、$180x-180y=3600$は両辺を180で割ると、

　$x-y=20$

　つまり連立方程式は以下のようになります。

\[
\left\{
\begin{array}{l}
x+y=240 \\
x-y=20
\end{array}
\right.
\]

　これを解くと$x=130,y=110$

　よって答えは、兄の歩く速さは130 m/分、弟の歩く速さは110 m/分

まとめ

　池の周りを歩く問題の考え方と解き方についてまとめます。

　池の周りを歩く問いで難しいのは、同じ方向に歩き出し、速く歩く方が遅く歩く方に追いつくことから式を立てることでしょう。

　逆にこれさえ分かればすぐに解けるようになるはずです。

　文章に書いてある状況をよくイメージして、正しく式を立てましょう。