得意な人と苦手な人に分かれる数学。

　小学校の算数はできたけど、中学で数学を始めた途端に苦手になってしまった……という人が多いのではないでしょうか？

　算数とは違い、数学の問題を解くには3つの力が必要です。

　それは、計算力・抽象化力ちゅうしょうかりょく・国語力です。

　数学が苦手な人は特に、抽象化力と国語力が欠けていることが多いです。

　それを克服できれば、数学が得意になりますよ！

抽象化力ってなに！？

数学に国語力なんていらないでしょ！？

　そう思ったそこの君！　ぜひこのまま読み進めていきましょう。

　思わなかった君も、そのまま下へどうぞ↓↓

　まずは、数学の問題を解くのに必要な力『計算力・抽象化力・国語力』について解説します。

　これは一番イメージが湧きやすいのではないでしょうか。

　計算力とは、具体的に言うと速く、正確に計算する力のことです。

　これは算数の時から必要な力ですね。数学をする上で最も基本的な力です。

　計算力が足りないな……と感じる人は、まずは計算力を鍛えれば数学のテストで点数UPを狙えますよ！

抽象化ちゅうしょうかなんて初めて聞いた！

　数学の問題、特に文章題では抽象化が必須です。と言われてもよくイメージできないでしょう。

　例として以下の問題を見てみましょう。

　このように、具体的な事柄を抽象的に表すことを抽象化と言います。

　問題文を見てください。奇数は1，3，5，7，・・・、偶数は2，4，6，8・・・のように具体的な数字で表されています。

　でも、このままじゃ奇数、または偶数を表す数字を無限に書かなきゃいけないので大変ですよね？

　だから文字を用いて抽象化するのです。

　みなさんが勉強する数学に限って言えば、抽象化とは問題文で表された日本語を数式で表すこと、と理解してください。

　ね？　こういうの苦手でしょ？

　中1の文字式の利用で躓いた人は、間違いなく抽象化力が弱いです。

　算数ではあまり求められることがなかった抽象化力ですが、数学には必須なので、中学生のうちに身につけておきましょう。

　極端に言えば、国語ができないと数学もできるようになりません。

俺は国語より数学のが点数高いけど？

　正確に言い直すと、日本語の文章を正しく理解できないと数学ができるようにならないのです。

　上で説明した抽象化は、問題文を理解していないとできないからです。

　日本語で何が書いてあるのかわからないのに、それを数式に直すことができないことは想像にかたくないですよね？

　さらに、みんなが大嫌いな証明問題も国語力が必要です。

　三角形の合同の証明問題を例としましょう。

　△ＡＢＣと△ＤＥＦが合同であることを証明しなさい、と言われたら、誰が読んでも納得するような文章を書いて証明しなければいけないのです。

　このように、数学の苦手を克服するには国語力を身につけるのが必須なのです。

　数学に必要な3つの力『計算力・抽象化力・国語力』について解説してきました。

　ここからは3つの力を踏まえて、単元ごとの苦手克服法を解説していきます。

　さて、みなさんの苦手な単元を当てて見せましょう。

　方程式の利用、一次関数・二次関数、証明問題　ですね？

　3つの力のうち、特に重要なのは抽象化力と国語力。

　数学が苦手な人はこの2つの力が弱いことが多いです。

　そうなると、方程式の利用、一次関数・二次関数、証明問題が苦手になりやすいのですよ。

　方程式の利用と言えば、一次方程式、連立方程式、二次方程式の利用があります。

　多くの中学生が難しく感じる単元です。

　特に一次方程式の利用は、中学に入ってから始めの難関と言えるでしょう。

　その時に適当にやり過ごしてしまうと、多くの人がその後もつまづいてしまいます。

　なぜなら、方程式の利用は数学に必要な力『国語力』と『抽象化力』が必要な単元だからです。

　ここでこの2つの力をつけるかつけないかが、今後の明暗を分けるのです。

　方程式の利用を解くには、次の3ステップを踏みます。

• 問題文を正確に理解する
• 方程式を立てる
• 計算をする

　方程式の利用を解けない人の多くは、1か2でつまづいています。

　1に必要な力は国語力、2は抽象化力です。

　つまり、方程式の利用が苦手な人は国語力か抽象化力のどちらか、もしくはその両方が弱いということです。

　まずは第一ステップ、問題文を正確に理解しましょう。

こんなの小学生でもわかるよ！

　書いてあることをただ認識するのではなく、方程式の利用を解くには、何と何が『＝』で結ばれるのかを理解しなくちゃいけないんです。

　上の例題では、何と何が＝で結ばれるでしょうか？

鉛筆とボールペンの代金の合計＝800円

になれば良いね！

　そこまでわかれば、後は『鉛筆とボールペンの代金の合計』を文字式に表せばOK。

　改めて問題と解答を出しておきます。

　方程式の利用は、1．問題文を正確に理解する、2．方程式を立てる　さえ出来てしまえば後は大したことないですね。

その1と2が出来ないんだよ(泣)

　ここからは1と2が出来るようになる方法を解説します。

文章題ってだけで嫌いだ……

　まず、1．問題文を正確に理解するには、国語力を上げる必要があります。

　国語力を上げる方法は簡単です。国語の授業をしっかり受けましょう。

　特に説明文で、筆者が何を言いたいのかを理解するようにします。

　授業で説明文を習う前に、自分一人で一通り読んでみましょう。

　難しく感じるかもしれませんが、内容をあらかじめ知っていれば、授業での理解度が上がりますよ。

　数学の成績だけでなく国語の成績も上がるので一石二鳥ですね！

問題文は理解出来ても、その後どうしたらいいかわからない……

　2．方程式を立てるには、文章に書いてあることを数式で表す必要があります。

　ここが苦手な人は、中1で習った『文字式の利用』から復習をしてみましょう。

　書かれていることを文字で表す＝抽象化は、中学生にとって決して簡単ではありません。

　抽象化に慣れるには、たくさん問題を解いて練習しましょう！

　ｘ、ｙ、グラフ、変域……。

　たくさんの記号や用語が出てくるので、見た目で圧倒されることもしばしば。

　ゆえに、関数自体が苦手！　と思っていてもただの食わず嫌いな人がいます。

　でも、一度よ～く考えてみると、｢なんだ、簡単じゃん！｣と思える単元です。

　嫌だ嫌だという前に、まずは一口食べてみませんか？

　一次関数・二次関数が苦手になる理由は次の2つです。

• 関数の意味をイメージしづらい
• ぱっと見で難しそうに見える

1つずつ解説します。

　さて、質問です。

　関数ってなんですか？

　改めて聞かれると難しいですよね。

　関数とは、数字を入力したらそれに対応する数字が出てくる機械のようなものです。

　例を出します。

　一次関数$y=2x+1$に、$x=3$と入力すると、$y=7$が出てきますよね。

　このように、xの値に関係してyの値が決まるとき『yはｘの関数である』と言います。

　別の言い方をすると、『yはxにともなって変わる数』です。

　このイメージが出来ていないと、関数の利用が解けないんです。

　まずは関係式を作ることを考えましょう。

　問題文には、ともなって変わる2つの量があります。

お風呂の水の量と、水を入れている時間だ！

　その通り！

　時間が経てば経つほど、お風呂の水は増えていくよね。

　時間と水の量は関係がある。つまり、関数の式に当てはめることができます。

始めからお風呂に入っている水はどうなるの？

　もちろん、始めからお風呂に入っている水も考える。といっても、そんなに難しくないですよ。

　お風呂の水の量をyℓ、時間をx分として式を考えると以下のようになります。

　$お風呂の水の量＝2ℓ×時間(分)+3ℓ(始めから入っていた水)$

　$y＝2ｘ+3$

　始めから入っていた水は足してあげればいいですよね。

　さて、式が分かれば上の問題は簡単に解けます。

　方程式の利用のように、関数でも抽象化力が必須です。

　関数を食わず嫌いになってしまうのは導入でも少し触れました。

　小学校の時まではあまり扱われなかったグラフを本格的に扱うのが一次関数・二次関数なんです。

グラフを見ただけで頭が痛くなる……

　そんな食わず嫌いなあなたは、まずは冷静に、簡単な問題からでもいいので取り組んでみましょう。

　学校の問題集や教科書で構いません。どれだけ時間が掛かっても良いので、一つずつ丁寧に解いてみます。

　落ち着いて考えれば、案外できる！と思うはずです。

最初からわからないよ……

　そんな人は、関数の意味や用語の意味が分かるかを確認しましょう。

　関数の意味は上で解説したので省略します。

　関数では用語がたくさん出てきますよね。

　変域、変化の割合、傾き、切片……

　これらの意味や公式を全部覚えていますか？

　知らない用語がたくさんあると、それだけで圧倒されてしまいますよね。

　こうなってしまうと、関数という単元自体に苦手意識をもってしまうのです。

　次の2ステップで苦手克服をしましょう。

　まずは食わず嫌いの克服が必須です。

　そのために、変域や変化の割合などの求め方、グラフの描き方など基礎・基本から一つずつ丁寧に仕上げていきましょう。

　これだけでもかなり関数アレルギーが軽減されますよ。

　簡単な問題からで構いません。少しずつ確実に解けるようになってください。

　食わず嫌いが克服できたら、関数の利用の問題にも取り組んでみましょう。

　関数の利用でも、文章を正確に理解し、関数の式を立てる必要があります。

　つまり、方程式の利用だけでなく関数でも抽象化力が必須ということはすでに述べました。

　方程式の利用と異なるのは、文章から式を立てるだけでなく、関数のグラフも描けないといけないということです。

　中学2年生まで、つまり一次関数までならグラフが描けなくてもなんとかなるでしょう。

　しかし、中学3年生で二次関数を勉強する頃にはグラフを描けるようにならないとミスをしやすくなってしまいます。

変域の数を代入して、ｙの値を出せば良いじゃん！

　一次関数ではそのようにしましたね。

　では、答えを聞いてみましょう。

答えは、

2≦y≦8

　はい、不正解です！

　これは、グラフを描かずに考えてしまう人の典型的な間違いなんですよ。

　二次関数y＝$\frac{1}{2}ｘ^2$のグラフを描いて、変域の所をペンでなぞってみましょう。

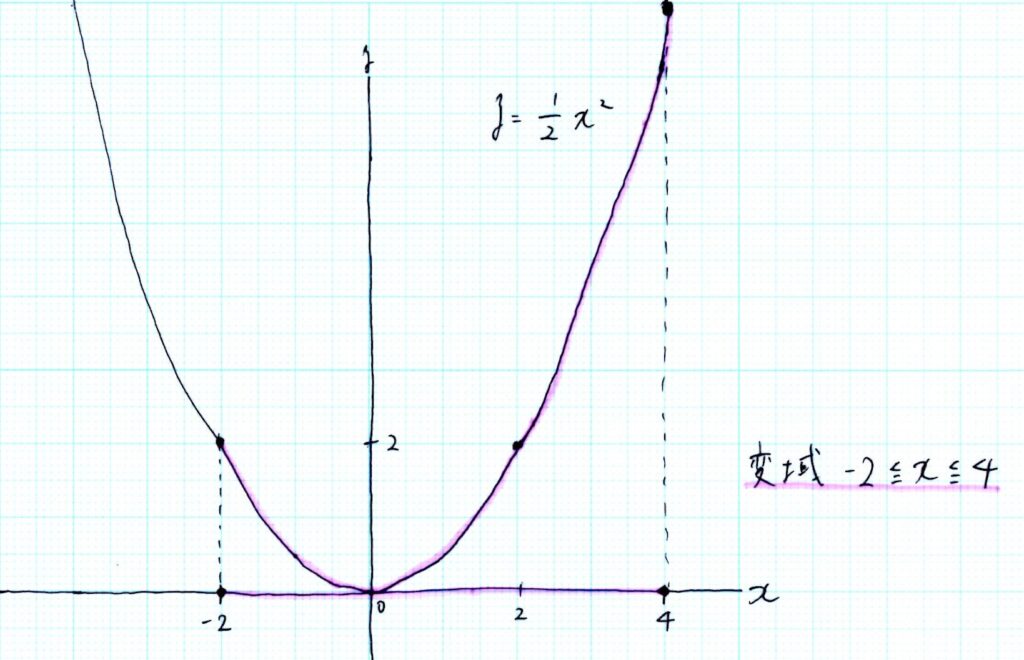
　変域が原点をまたいでいるのがわかりますか？

　つまり、-2≦x≦4の範囲ではyの最小値は0です。

　よって、答えは0≦y≦8です。

　証明問題というとどんなイメージがあるでしょうか？

数学なのに文章を書かなきゃいけない……

　小学校で習った算数ではまず出てこなかったタイプの問題ですよね。

　文章(問題文)を読んで、文章を書かなくてはいけない。それだけで圧倒されてしまう中学生が非常に多いです。

　でも、中学でならう証明問題は、型さえ覚えてしまえば入試まで役に立つので、一度マスターしてしまえば入試で得点源になります。

　ここからは『図形の証明』と『文字式を用いた証明』について解説します。

　図形の証明は中2、文字式を用いた証明は中3の単元です。

　図形の証明にしろ文字式を用いた証明にしろ、文章を書かないといけないですよね。

　つまり、証明問題は国語力がないと満点を取れないのです。

　また、文字式を用いた証明では国語力だけでなく抽象化力が必要です。

　こうして見ると難しそうに感じるでしょうか？

　文章をたくさん書かなければいけないというだけで苦手意識を感じてしまう中学生が多いんです！

　高校入試の模試では、証明問題は考える前に諦めてしまう人がいます。

　そうです。関数と同じように、食わず嫌いをしてしまう中学生がたくさんいるのです。

　　証明問題も食わず嫌いの中学生が多発する科目なので、まずは少しずつ慣れていくことから始めましょう。

　教科書の例題レベルの簡単な問題でいいので、一つずつ丁寧に解いていきます。

どうやって解答を書いたらいいかわからないよ

　慣れないうちは解答を丸写ししても構いません。

　証明の基本的な流れを身につけるのと、どうしたらみんなに伝わる文章が書けるのかを勉強しましょう。

　中2で合同証明、中3で相似の証明を習います。

　図形の証明は国語力があれば解くことができます。つまり、証明の文章を書くことができれば後は基礎知識の暗記をすれば問題ありません。

　合同条件や相似条件、錯覚・同位角といった図形の性質をしっかり覚えましょう。

　中1で文字式の利用を習い、中3では文字式を用いた証明を習います。

　これは国語力だけでなく、問題文に書かれていることを文字式で表す抽象化力が必要です。

　この単元でつまづいている人は、方程式の利用も苦手ではないでしょうか？

　受験まで時間がある冬休み前までには抽象化力を身につけておきましょう。

　数学の苦手を克服するには、抽象化力と国語力がいかに大切かわかってもらえたでしょうか？

　中学生のみなさんは、計算はよくできます。

　しかし、日本語の文章から式を立てる抽象化、自分の言いたいことをわかりやすく伝える国語力が必要な問題が苦手な人がとても多いです。

　数学の本質は速く正確に手で計算ができることではなく、自分の頭で考え、一つの答えを出すことにあります。

　日本の明るい未来のため、そして数学を心から楽しむために、今日から苦手を克服していきましょう！