【中3数学】y=ax^2の利用『振り子』の式と問題の解き方を解説

　$y=ax^2$の利用『振り子』は、関係式が難しく見えるだけでなく、聞きなじみのない『周期』という言葉が出てきたりするため勉強するのが嫌になってしまいますよね。

　この記事では$y=ax^2$の利用『振り子』の問題を解くために必要な、糸の長さと周期の関係式の解説から始めます。

　図を用いて言葉の意味から解説しているので、安心して読んでくださいね

　その後で振り子の問題を解いて理解を深めていきましょう。

振り子の糸の長さと周期の関係式

　振り子の糸の長さと周期の関係式を見ていきましょう。

　振り子の糸の長さは周期の2乗に比例するので、以下の式が成り立ちます。

周期ってなに？

　周期とは振り子が一往復する時間のことです。

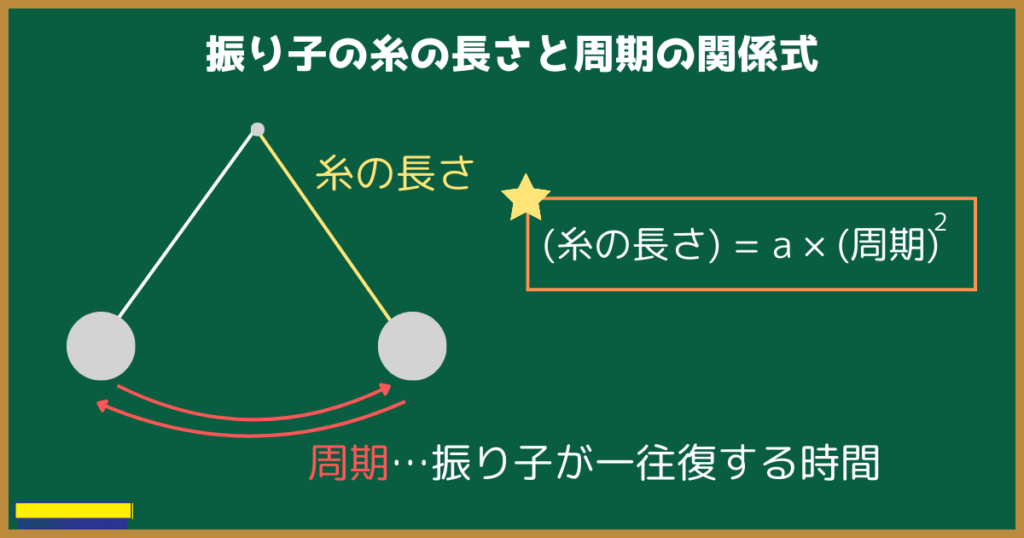
この式『$(振り子の糸の長さ)=a×(周期)^2$』で言っている通り、

周期が長ければ長いほど振り子の糸は長いってことだね！

【例題】$y=ax^2$の利用『振り子』

　ここからは】$y=ax^2$の利用『振り子』の例題をやっていきましょう。

　①について。

　振り子の糸の長さが周期の2乗に比例するので、振り子の糸の長さをy、周期をxとすると『$y=ax^2$』の形になります。

でもaがわからないよ？

　問題文を読むと振り子の糸の長さが3mのとき、周期は6秒と情報があるので、それを『$y=ax^2$』に代入すればaを求められます。

　$y=ax^2$より

　$3=a×6^2$

　$a=\frac{3}{36}$

　$a=\frac{1}{12}$

　よって振り子の糸の長さをy、周期をxとするとき、yをxで表すと、$\color{red}{y=\frac{1}{12}x^2}$

　②について。

　①より、糸の長さと周期の関係式は$y=\frac{1}{12}x^2$だとわかったので、周期が18秒のときの振り子の糸の長さは、この式にx=18を代入すれば求められます。

　$y=\frac{1}{12}x^2$より

　$y=\frac{1}{12}×18^2$

　$y=\frac{1}{12}×324$

　$y=27$

　よって糸の長さは27m

　③について。

　今度は振り子の糸の長さがわかっていて、周期を求める問いですね。

ということは、

$y=\frac{1}{12}x^2$にy=12を代入して、

xを求めればいいんだね。

　$y=\frac{1}{12}x^2$より

　$12=\frac{1}{12}x^2$

　$x^2=144$

　$x=±12$

あれ？

x=±12ってことは、周期は12秒と-12秒…？

　周期は時間なので、当然正の数です。

　つまり、x>0なので答えは12秒です。

まとめ

　$y=ax^2$の利用『振り子』は、言葉の意味と関係式さえ理解できれば、そんなに難しくありません。

　文章題というだけでめげそうになるかもしれませんが、ぐっとこらえて式と言葉を理解しましょう。