【二次関数】yの変域で『0』がでる理由はグラフでわかる！丁寧に解説【0≦y≦a/a≦y≦0】

　二次関数の変域を求める問いで、このような疑問をもつ人は多いでしょう。

なんでyの変域に0が出てくるの？

　そう思うあなたはずばり、二次関数のyの変域を、xの変域を代入しただけで求めていますね？

　一次関数の変域を求める時はそれでも良いでしょう。しかし、二次関数ではそうはいかないのです。

　二次関数の変域で0が出てくる理由は、二次関数のグラフを描けばわかります！

　どういうこと？　と思ったあなた！　この記事ではそれを詳しく解説していま

yの変域で0が出てくるのはxの変域が0をまたぐとき

　yの変域で0が出てくるのはどんなときでしょうか。

　それは、xの変域が0をまたぐときです。

　xの変域が0をまたぐとは、変域が$-1≦x≦3$や$-5≦x≦8$などのときです。

　ことのき、x=0になることもあるということです。

　では、x=0のときのyはいくつでしょうか？

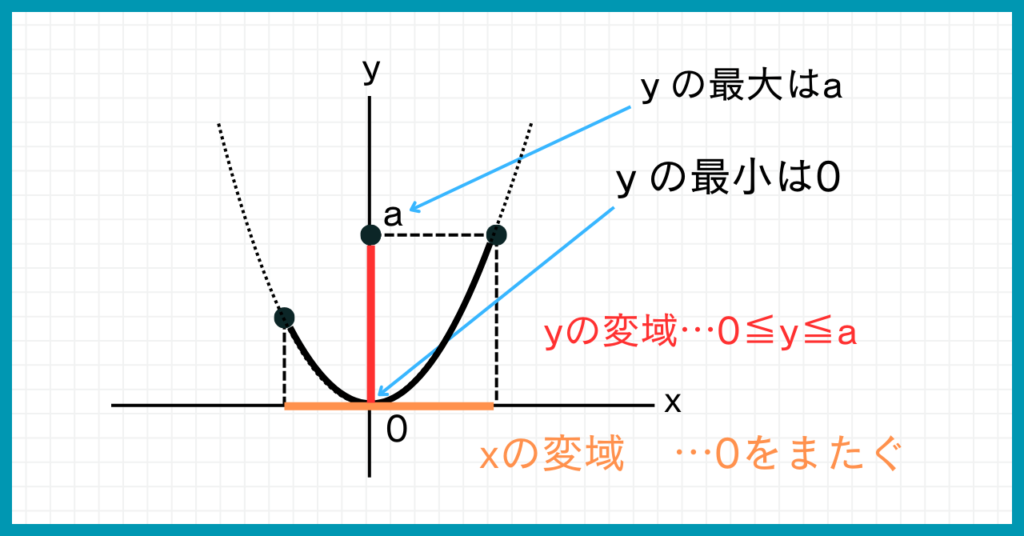
　上の図を見ると、x=0のときにy=0を通っていますよね。

　つまり、上の図のグラフでいうと、yの最小値は0です。

　つまり、yの変域は0≦y≦aのように表されるのです。

【例題で解説】グラフを描いて二次関数の変域を求める方法

　ここからは具体的な問題を解きながら、yの変域に0が出てくる問いを解説します。

【例題①】yの変域が0≦y≦aまたはa≦y≦0になる問い

　①について。

　まずは$y=x^2$のグラフをざっくりと描きます。

　xの変域も反映させましょうね。

グラフがどんな形になって、xの変域がどこからどこまでなのかがわかればいいから、

ざっくり描けばいいんだね。

　グラフを描くと、yの最小値は0であることがわかるでしょう。

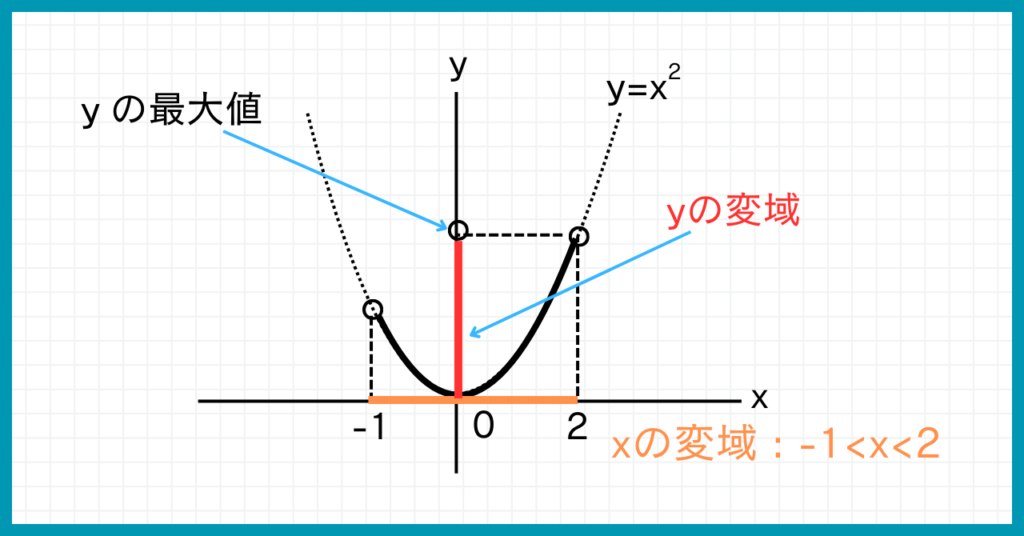
　では、yの最大値はxがいくつのときでしょうか？　グラフを見て考えましょう。

x=2のとき、yの値が一番大きくなるね！

　$y=x^2$より、x=2のときのyの値は、$y=2^2=4$です。

　よってyの最大値は4です。

　以上より、yの変域は0<y<4です。

　次に②について解説します。

　まずは$y=-2x^2$のグラフを描きます。

今度は上が閉じたような形になるね！

　①の例題とは逆で、y=0のときにyの値が最大になります。

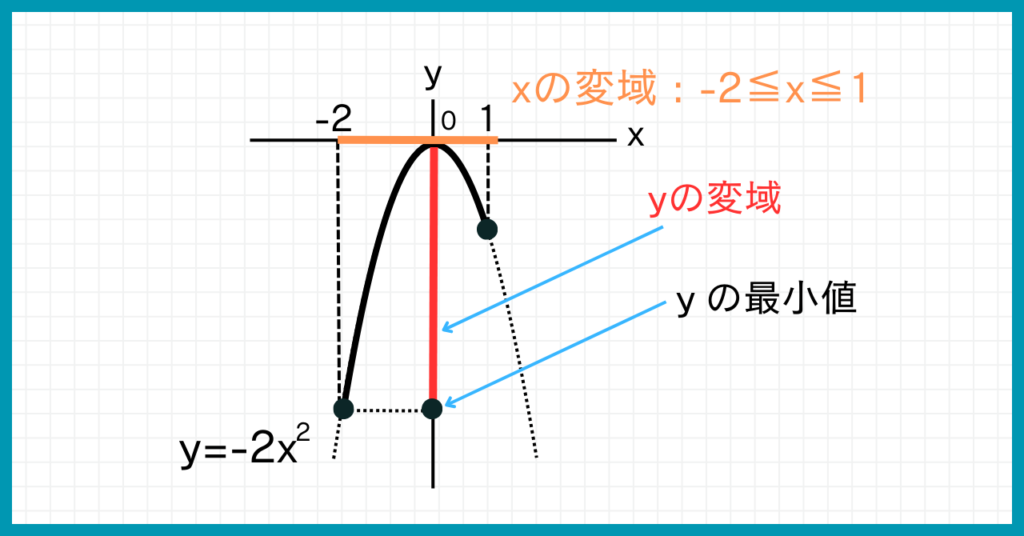
　では、yの最小値はxがいくつのときでしょうか？　グラフを見て考えましょう。

x=-2のとき、yの値が一番小さくなるね！

　$y=-2x^2$より、x=-2のときのyの値は、$y=-2×(-2)^2=-8$です。

　よってyの最小値は-8です。

　以上より、yの変域は-8≦y≦0です。

【例題②】yの変域がa≦y≦bになる問い

　ここからは、xの変域が0をまたがないとどうなるか、例題を用いて解説します。

　変域を求める問いでは始めにグラフを描きます。

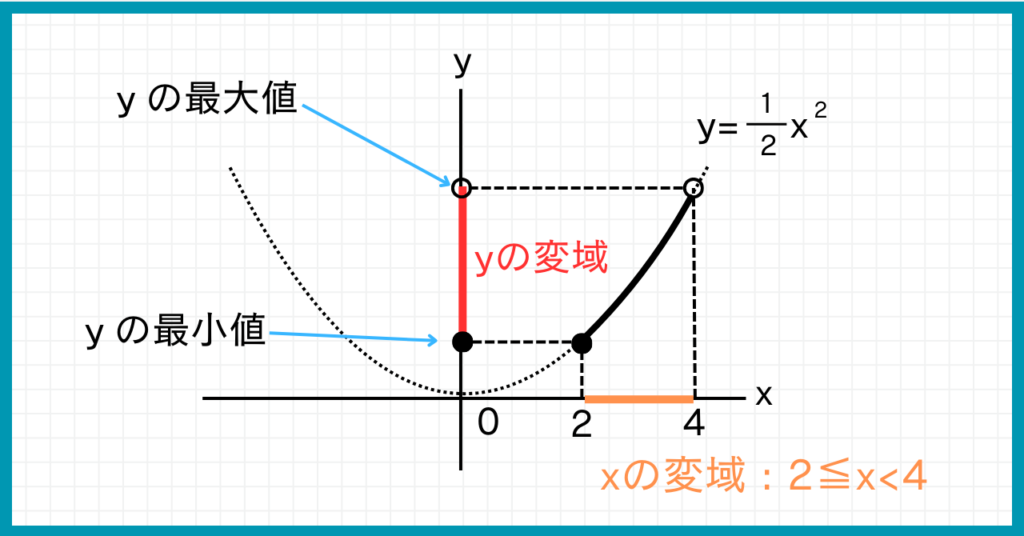
　グラフを見ると、yの変域に0が含まれないことがわかりますね。

　では、xがいくつのとき、yの値は最小、または最大になるでしょうか？

x=2のときにyの値が最小、

x=4のときにyの値が最大だね！

　$y=\frac{1}{2}x^2$より、

　x=2の時は$y=\frac{1}{2}×2^2=2$

　x=4のときはy=8

　以上より、yの変域は2≦y<8です。

まとめ

　二次関数において、yの変域で『0』が出てくる理由についてまとめます。

　二次関数の変域を求める問いでは、グラフを描いて考えることが重要です。

　一次関数の変域を求める問いで、単に代入しただけで解いていた人にとってはグラフを描くのは面倒に感じるかもしれません。

　しかし、そもそも代入しただけで変域を求められると思っているならば、それは問題の本質を理解しているとは言いがたい状態です。

　ミスを防止する意味でも、変域をきちんと理解して解くという意味でも、必ずグラフを描いて問題を解きましょう。