【超簡単】正負の数の加法・減法(足し算・引き算)のシンプルなやり方を解説
中学校の数学で最初に習う『正負の数』の加法と減法。
小学校の算数には無かったルールがいきなり登場してきて、中1のあなたが混乱してしまうのも無理はありません。
そんなあなたにおすすめしたいのは、かっこの外し方を真っ先に覚えることです。
さらに数直線をイメージすれば、以下のような正負の数の加法・減法を簡単に解けるようになります!
$(-1)-(+2)$
$(-1)+(+3)$
一方、正負の数が混ざった式でかっこを付けたまま計算するとなると、正負の数の加法・減法のルールがごちゃごちゃしています。
しかしこんなルールを覚えなくても、かっこの外し方を理解し、数直線をイメージするだけで正負の数の加法と減法をできるようになるのです!
この記事ではまず、『正負の数の式』でかっこを外す方法を解説します。
次に数直線と正負の数の関係をイメージできるように解説し、正負の数の加法・減法を数直線を用いて解けるようにします。
かっこの外し方と数直線のイメージを踏まえて、正負の数の加法・減法の簡単なやり方を解説します。
最後に基礎問題4パターンの例題を用いて、具体的な解き方を解説します。
正負の数の加法・減法をするために押さえること2選
正負の数の加法・減法は難しいルールを覚えなくても、以下の2つを押さえれば簡単に解けるようになります。
以下で詳しく解説します。
①式のかっこを外す(外し方)
正負の数の加法・減法では、以下のようにかっこのついた式が出てきます。
$(+3)-(-2)$
正負の数の加法・減法をするときは、まずはこのかっこを外してしまいましょう。

①について
例えば$(+3)+(+2)$だったらかっこを外したあと、
$+3++2$みたいになっちゃダメってこと?
上の例だと、『+』と『+』が直接並んでいるからダメです。
『+』と『+』が直接並ばないようにかっこが付いていたわけです。
では、かっこを外したときに符号が直接並んでしまうときはどうすればいいか。
それは、以下のルールに則って符号を変化させることで解決します。
正負の数のかっこの外し方は4パターンあるように見えて実は2パターンです。
例えば$(+3) + (+4)$のように『+ +』と同じ符号が並んでいるときは、かっこを外したら以下のように『+』になりますよね。
$(+3) + (+4)=3 + 4$
もう一度『かっこの外し方』を見て、同じ符号の時は『+』で、異なる符号のときは『-』になっていることを確認しましょう。
②数直線で正負の数をイメージする
正負の数の加法・減法は、数直線上の移動だけで理解できます。
そのためにはまず、数直線をイメージできるようになりましょう。
数直線とは、その名の通り数が順番に並んだ直線のことです。
小学校までは0が一番小さな数として扱われていましたね。
しかし中学校からは0よりも小さな数――負の数が登場したので、数直線は以下のようになります。
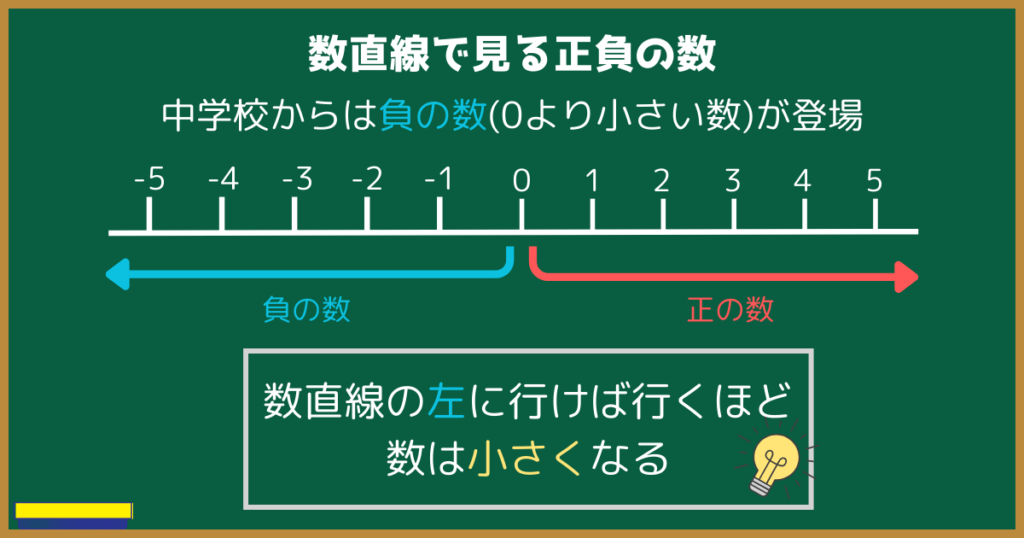
数直線の右に行けば行くほど、数は大きくなります。
逆に、数直線の左に行けば行くほど、数は小さくなります。

例えば『-4』と『-1』なら
『-4』の方が数直線の右側にあるから
『-1』より『-4』の方が小さいんだね!
つまり、加法(足し算)をすることは数直線の右に進むことです。
逆に、減法(引き算)をすることは数直線の左に進むということなのです。
正負の数『加法・減法』のやり方
ここからはいよいよ、正負の数の加法・減法のやり方を解説します。
正負の数の加法・減法の手順は以下です。
この手順通りに、正負の数の加法・減法をやっていきましょう。
①正しくかっこを外す
正負の数の加法・減法のやり方を、以下の例題を使って解説します。
問題
次の計算をしましょう。
- $(+1)+(+2)$
- $(+3)-(+2)$
まずはかっこを外しましょう。
問題
かっこを外したら以下のようになる。
- $(+1)+(+2) = 1 + 2$
- $(+3)-(+2) = 3 – 2$
かっこを外してしまえば、あとは簡単な算数の問題ですね。
しかしあえて、これらの計算を数直線上で表してみましょう。
②加法・減法を数直線上の移動でイメージする
まずは①$1 + 2$から見ていきましょう。
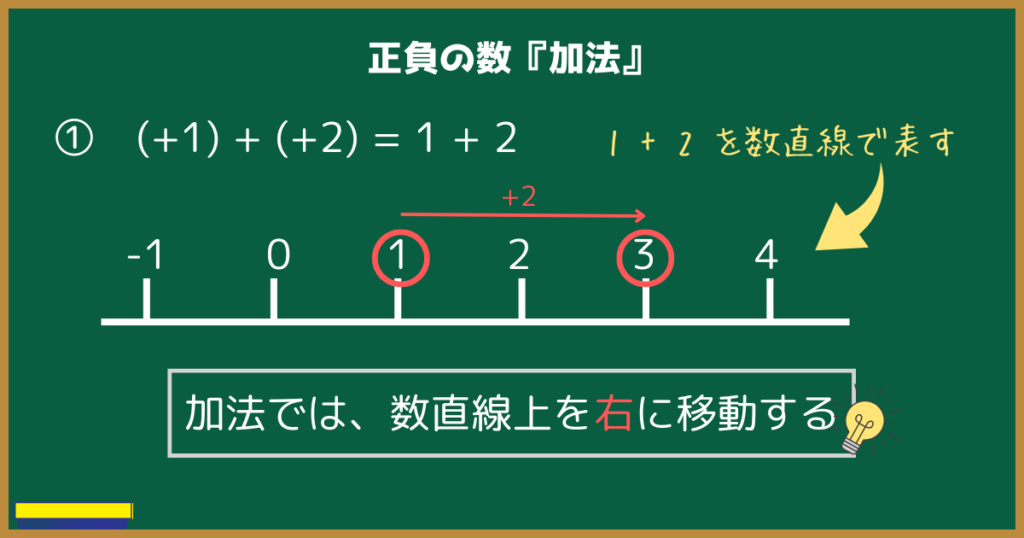
$1+2$は言葉で説明すると、1に2を足すことですよね。
数直線上では、1から右に向かって2だけ進んで、3に到達していますね。
つまり、加法とは数直線上で右に進むことなのです。
次に②について見ていきましょう。
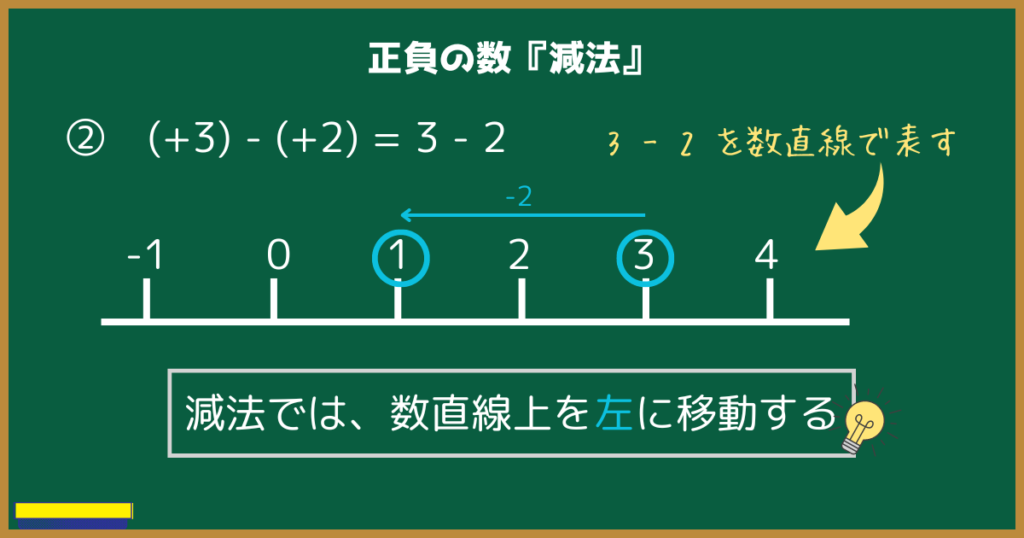
$(+3)-(+2)$は言葉で説明すると、3から2を引くことです。
数直線上では3から左に向かって2だけ進んで、1に到達しています。
つまり、減法とは数直線上で左に進むことです。
このように、加法・減法は数直線上の移動であると考えられます。
この考え方ができれば、正負の数の加法・減法を簡単に攻略できますよ!
【基礎4パターン】正負の数『加法・減法』を例題を用いて解説
ここからは本格的に、中学範囲の加法・減法を解説します。
問題
- $(+1)+(-3)$
- $(-1)-(+2)$
- $(-1)+(+3)$
- $(-4)+(+3)$

まずはかっこを外すんだよね!
上の問題のかっこを外した式は以下です。
問題
かっこを外したら以下のようになる。
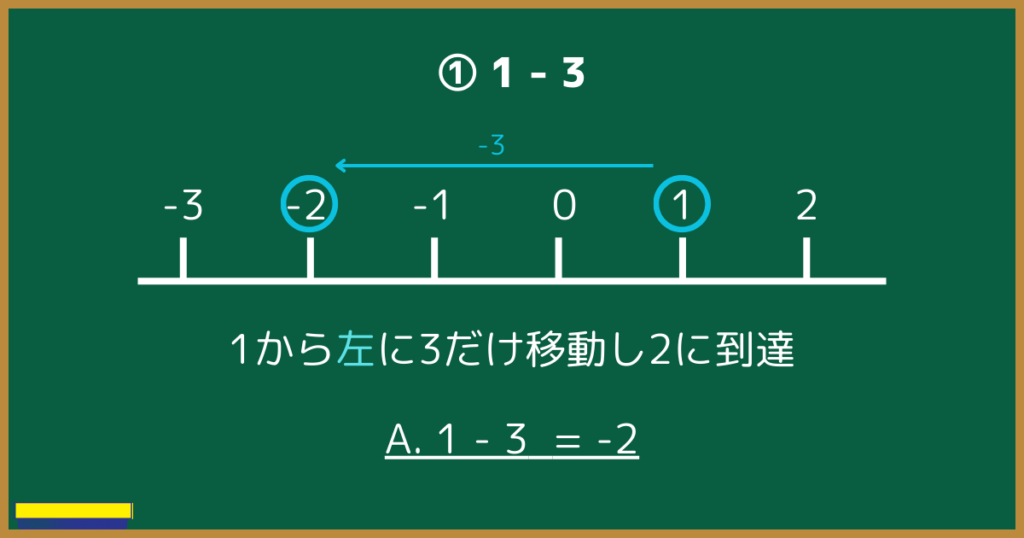
- $1-3$
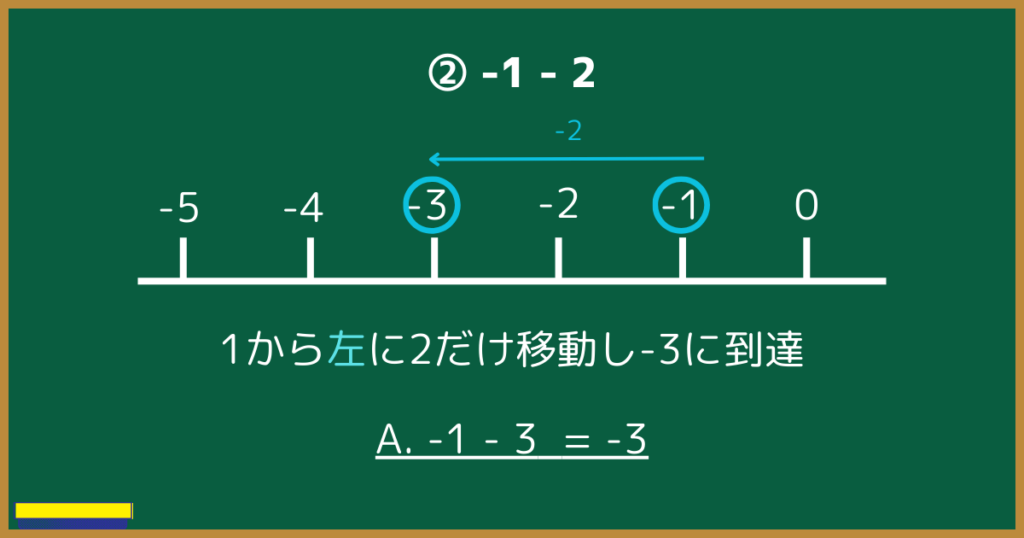
- $-1-2$
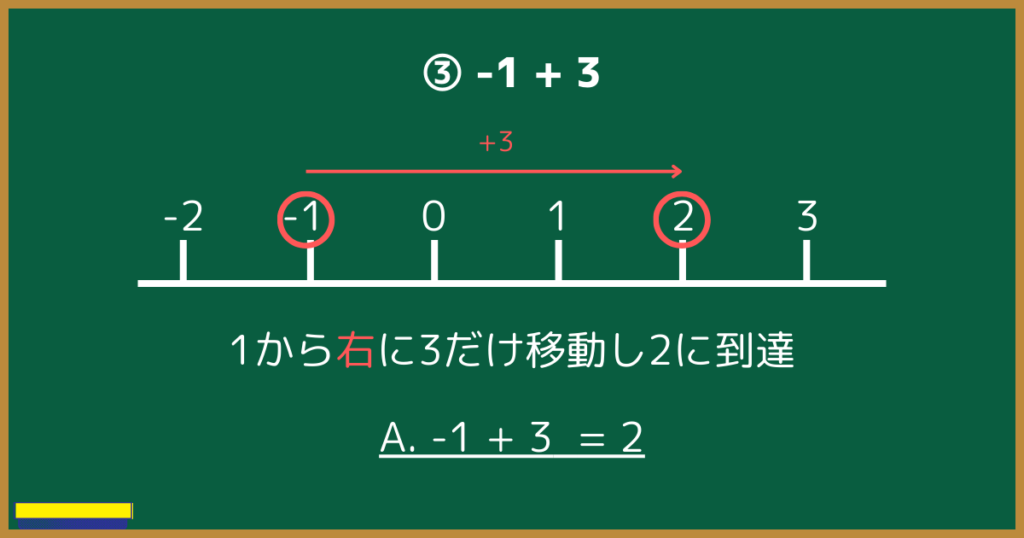
- $-1+3$
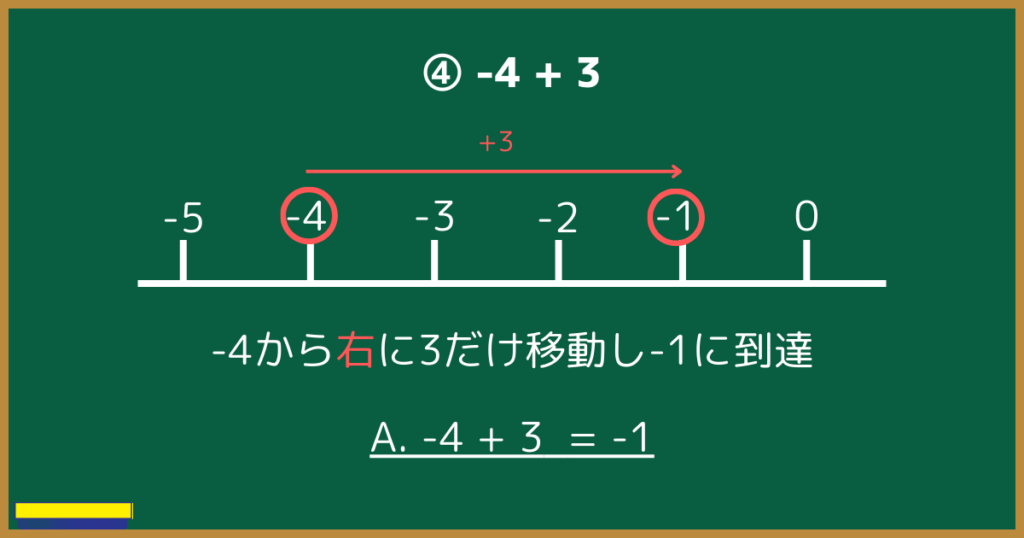
- $-4+3$
かっこを外すルールは、同符号なら『+』、異符号なら『-』にすることでしたね。

かっこを外した後は、加法・減法の数直線上の移動を考えればいいんだね
①(正の数)+(負の数)
①は、正の数から0をまたいで負の数になる問いです。
②(負の数)+(負の数)
②は、負の数からさらに引き算(減法)をしています。
つまり、-1よりさらに小さな負の数が答えになります。
負の数は、数字が大きくなればなるほど、数は小さくなります。

例えば-1と-10を比べると、
$-10<-1$
だね
③(負の数)+(正の数)【正の数が大きい】
③は負の数から0をまたいで正の数になる計算です。
④(負の数)+(正の数)【正の数が小さい】
最後に④は、負の数に足し算(加法)をした結果、負の数になる計算です。
以上のように、正負の数の加法・減法は数直線の移動で説明できます。
慣れてきたら、数直線を頭に思い浮かべるだけで計算できるように計算練習をしましょう。
まとめ
正負の数『加法・減法』の解き方をおさらいしましょう。
正負の数の計算は、中学だけでなく高校・大学と数学を学ぶ上で必ずできるようにならないといけません。
算数にはなかった負の数の概念に戸惑うこともあるかと思いますが、数直線をイメージできれば難しいことはないのです。
学校のワークや市販の問題集でたくさん計算練習をして、数学の世界に慣れてくださいね。


コメントを残す