【中3】これだけ押さえて!三角形の相似条件の覚え方【相似は拡大縮小コピー】

中学3年生のあなた! 三角形の相似条件は完璧ですか?
相似の単元では証明問題があります。
ということは、まずは相似条件を覚えなくてはいけませんよね。

三角形の相似条件が覚えられない

合同条件とごちゃごちゃになっちゃう
三角形の相似の証明は、合同の証明と同じで高校入試でよく出題されます。
中3のあなたは、過去問や模試で相似の証明が出題されているのを見た瞬間に解くのを諦めてしまうのではないでしょうか?
もしくは頑張って解答しても得点ができないのではないですか?
証明問題は配点が高いので、相似条件が覚えられなくて得点できないなんてもったいない!
この記事を読んで、ぜひ三角形の相似条件を覚えましょう。
丸暗記ではなく、なぜそのような条件で相似だとわかるのか?を理解しながら覚えられますよ!
まずは相似とは何かを確認しましょう。
その後、なにかと混同しがちな合同との違いを確認します。
相似とは何か
相似とは、形は同じだけど大きさが違う二組の図形のことです。
つまり、拡大・縮小コピーの関係なのだと覚えておきましょう。
まったく同じ形、同じ大きさの2つの三角形を思い浮かべてみてください。
そのうち片方を拡大もしくは縮小コピーすると、角度と辺はどうなるでしょうか?

拡大、縮小コピーをしても図形の角の大きさは変らないね

2倍、3倍・・・と拡大コピー、
もしくは\frac{1}{2}倍、\frac{1}{3}倍・・・と縮小コピーをしたら、辺も2倍、3倍・・・もしくは\frac{1}{2}倍、\frac{1}{3}倍・・・となるね!
つまり、相似な図形は辺の比が等しくなります!

角についてはわかったけど、辺の比についてはよくわからないな
そんな人は以下の図を見てイメージしてみましょう。
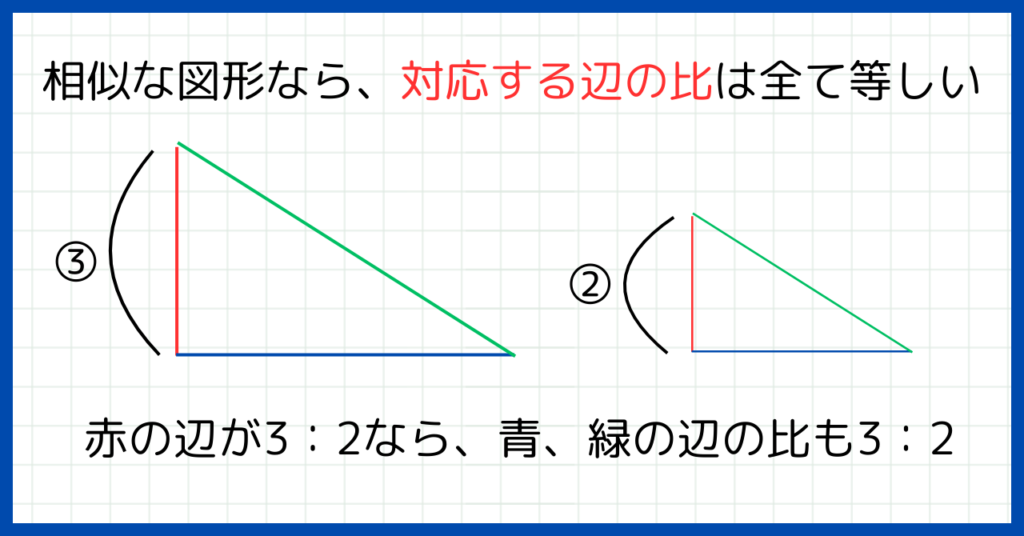
相似な図形の特徴
- 対応する角の大きさはそれぞれ等しい
- 対応する辺の比はそれぞれ等しい
相似の意味をしっかり押さえることで、相似条件を理解しやすくなりますよ!
相似と合同の違いは?
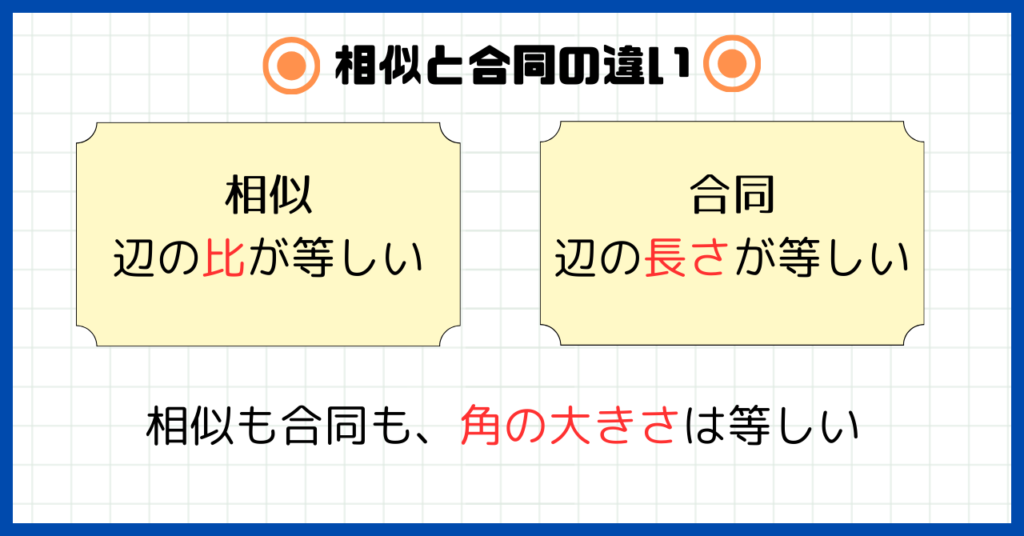
相似は形が同じだけど大きさが違う二組の図形のことでした。
それに対して合同は、形も大きさも同じ二組の図形のことです。
相似が拡大・縮小コピーの関係なら、合同は『そのままコピー』の関係です。
合同な図形の特徴
- 対応する角の大きさはそれぞれ等しい
- 対応する辺の長さはそれぞれ等しい
つまり相似と合同の違いは、対応する辺の関係にあるのです。
合同について復習したい人はこの記事を見てください。
三角形の相似条件3つを確認
3つの相似条件を確認しておきましょう。
三角形の相似条件
- 3組の辺の比が全て等しい
- 2組の辺の比が等しく、その間の角が等しい
- 2組の角がそれぞれ等しい
2つの三角形が相似であることの証明は、三角形の相似条件のうち1つを示すことができればOKです。
なぜその条件で相似だと証明できるのか?ひとつひとつ解説
相似条件が覚えられないあなたのために、なぜこの条件で相似であると証明できるのか?を理解できるよう解説していきます。
相似は拡大・縮小コピーの関係であることを思い出しましょう。
これだけ押さえていれば、相似条件も簡単に理解できますよ。
3組の辺の比が全て等しい
相似な三角形同士は拡大・縮小コピーの関係です。
ということは、ある辺と、それに対応する辺の比は全て等しくなりますよね。

つまり、3組の辺の比が全て等しいことがわかれば、相似であると言えます。
2組の辺の比が等しく、その間の角が等しい
2組の辺の比が等しく、その間の角が等しいとは、以下の図のような状態のことです。
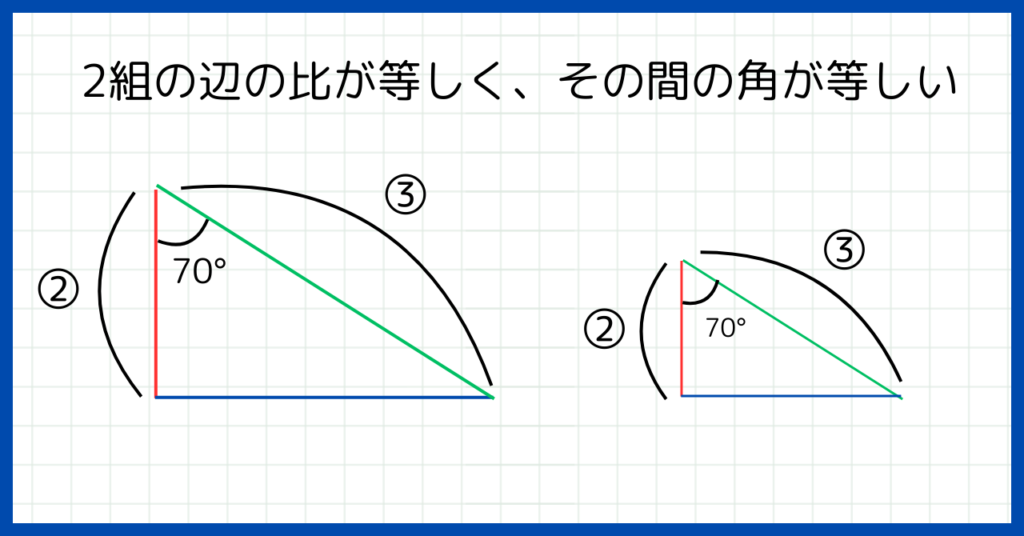
比が分かっている二組の辺(上の図で言うと赤と緑の辺)の間の角が決められていたら、他の辺(青の辺)は2組の辺の終点を結べば書くことができますよね。
つまり、2組の辺の比とその間の角が決まれば他の辺が自動的に決まるので、2組の辺の比が等しく、その間の角が等しいなら相似であると言えるのです。
2組の角がそれぞれ等しい
相似な図形同士は拡大・縮小コピーの関係です。
つまり、三角形の大きさは異なっても角度は同じなのです。
2組の角がそれぞれ等しいとは、以下の図のような状態です。
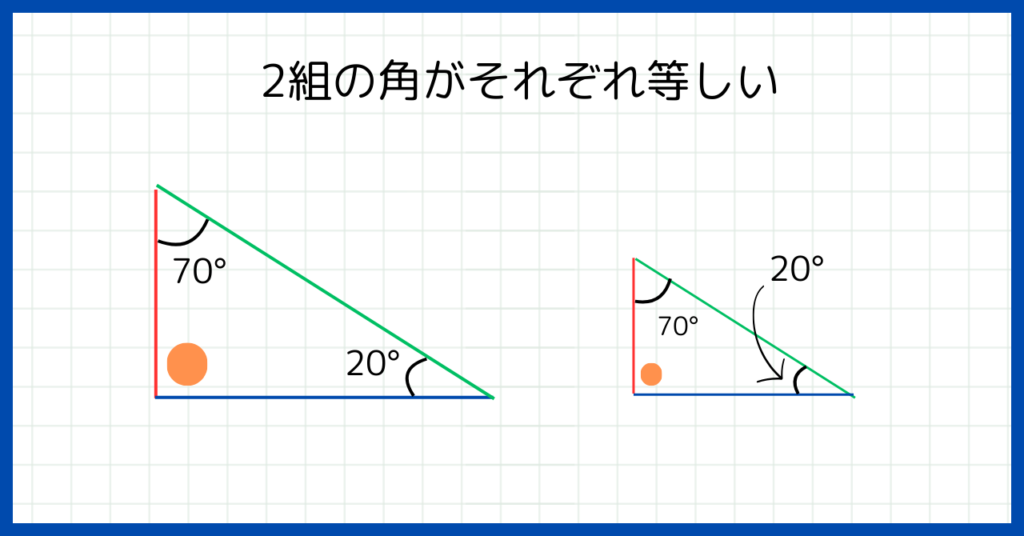
三角形の内角の合計は180°と決っています。
つまり、対応する二組の角が等しいことがわかれば、自動的に他の角も等しいということになります。
上の図のどちらの三角形も、オレンジの○が90°になりますよね。
つまり、2組の角がそれぞれ等しいことがわかれば他の角も等しいことがわかり、相似であると言えるのです。
まとめ
相似とは拡大・縮小コピーの関係です。
このことさえ理解していれば、三角形の相似条件を理解することに繋がり、証明問題が解けるようになります。
中学生のみなさんの中にはまだ拡大コピーや縮小コピーをしたことがない人がいるかと思います。
相似のイメージがまだ湧かない!という人は、コンビニにあるコピー機でも拡大コピーや縮小コピーができるので、やってみるといいでしょう。

コメントを残す