【小学生でもわかる】等差数列と等比数列『一般項の公式』の覚え方！公式の成り立ちを解説

　等差数列と等比数列の公式を丸暗記しようとはしていませんか？

　数学Bの『数列』ではたくさんの公式が出てくるので、それらを全て丸暗記しようとするといずれ限界が来てしまいます。

　そこでまずは、等差数列と等比数列の一般項がなぜあの形になるのか？を理解しましょう。

公式の成り立ちを理解するなんてめんどくさい！

　実は等差数列と等比数列『一般項の公式』は、中学受験をする小学生でも理解しているのです！

　高校生のあなたに理解できないはずがないですよね？

　難しい公式を丸暗記するだけ損！　わかりやすい説明を聞いて、公式をラクに覚えていきませんか？

数列の公式は小学生でも知ってる！？

　あなたが苦しんで覚えようとしている数列の一般項の公式、実は小学生でも知っています。なぜなら中学受験の算数で出題されるからです。

　といっても、$a_{n}=a_{1}+(n-1)d$や$a_{n}=a_{1}･r^(n-1)$のような記号で出てくるわけではありません。というか、小学生には文字では説明できません。

　ならどうしているのかというと、等差数列はこういう数列だよと具体的に説明しています。

　逆に言えば、数列の一般項の公式は、具体例を用いて小学生でも理解できるように説明できるのです。

　それなら、難しい文字列である公式の丸暗記するだけ損だと思いませんか？

　小学生でも理解できる説明を聞いて、公式を理解して忘れにくくしましょう。

等差数列の公式を解説

　まずは等差数列の公式を確認し、その次に成り立ちをわかりやすく解説します。

等差数列の公式$a_{n}=a_{1}+(n-1)d$

　まずは等差数列の公式を確認しましょう。

等差数列の一般項の公式が成り立つ理由

　そもそも等差数列とはなにか、あなたは説明できますか？

　等差数列の一般項の公式が成り立つ理由を読む前に、まずは等差数列とはなにかを確認しましょう。

　等差数列とはなにかをわかったところで、等差数列の一般項の公式が成り立つ理由を見ていきましょう。

　等差数列の一般項の公式『$a_{n}=a_{1}+(n-1)d$』は、数列の『n番目の数』を表しています。

　なぜn番目の数が『$a_{n}=a_{1}+(n-1)d$』で表されるのかを調べるため、○番目の数を具体的に求めてみましょう。

　この数列の公差はいくつでしょう？

公差は『3』だね！

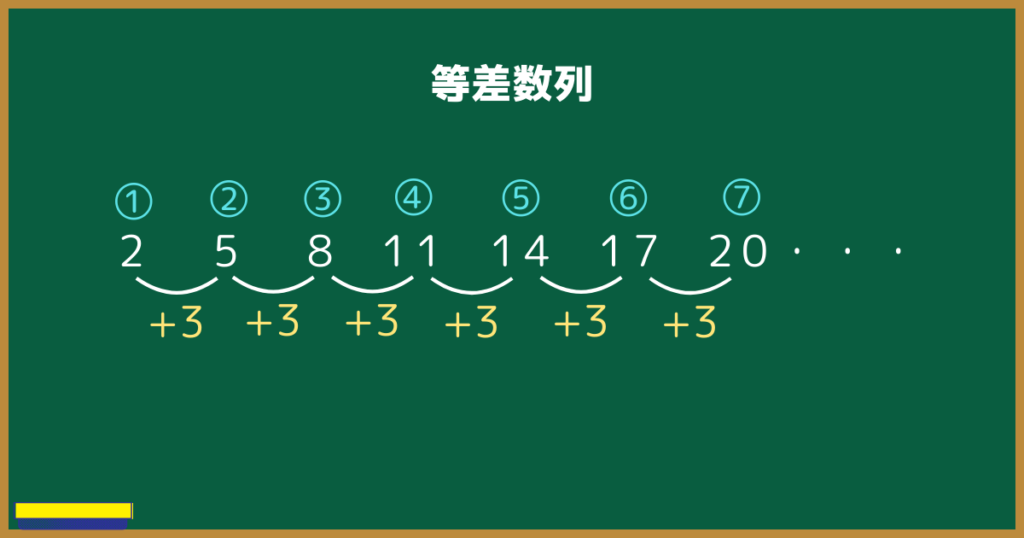
　○番目の数を具体的に求めるためには、初項2に、公差3をいくつか足します。

　ここでは3番目、5番目、7番目の数を求めてみます。

• 3番目の数($a_{3}$)は初項2に、公差3を2つを足す
  ⇒$2+3×2＝8$

　同じように上の図を見ながら、5番目と7番目の数を求めましょう。

• 5番目の数($a_{5}$)は初項2に、公差3を4つを足す
  ⇒$2+3×4＝14$
• 7番目の数($a_{7}$)は初項2に、公差3を6つを足す
  ⇒$2+3×6＝20$

　何番目の数でも、初項に公差を足すことは変わりません。

　では、公差をいくつ足すか？

　3番目の数を求めるときは公差を2つ足す

　5番目の数を求めるときは公差を4つ足す

　7番目の数を求めるときは公差を6つ足す

『○番目の数よりも1小さい数』だけ公差を足すんだね！

　では、『n番目の数』を求めるにはどうしたら良いでしょうか？

　初項$a_{1}$、公差dの数列のn番目の数を求めるには、初項$a_{1}$に、公差dを$n-1$つ足すと、式は以下のようになります。

　$a_{n}=a_{1}+(n-1)d$

　これが等差数列の一般項の公式です。

等比数列の公式を解説

　まずは等比数列の一般項の公式を確認し、その次に成り立ちをわかりやすく解説します。

等比数列の公式$a_{n}=a_{1}･r^{n-1}$

　まずは等比数列の公式を確認しましょう。

　等比数列とはなにかをわかったところで、等比数列の一般項の公式が成り立つ理由を見ていきましょう。

等比数列の公式が成り立つ理由

　等差数列の公式が成り立つ理由とほとんど同じです！

　でも理由を説明する前に、そもそも等比数列とはなにかを確認しておきましょう。

　等比数列の一般項の公式『$a_{n}=a_{1}･r^{n-1}$』は、数列の『n番目の数』を表しています。

　なぜn番目の数が『$a_{n}=a_{1}･r^{n-1}$』で表されるのかを調べるため、○番目の数を具体的に求めてみましょう。

　この数列の公比はいくつでしょう？

公比は『2』だね！

　○番目の数を具体的に求めるためには、初項3に、公比2をいくつか掛けます。

　ここでは3番目、5番目、7番目の数を求めてみます。

• 3番目の数($a_{3}$)は初項3に、公比2を2つ掛ける
  ⇒$3×2^2＝12$

　同じように上の図を見ながら、5番目と7番目の数を求めましょう。

• 5番目の数($a_{5}$)は初項3に、公比2を4つ掛ける
  ⇒$3×2^4＝48$
• 7番目の数($a_{7}$)は初項3に、公比2を6つ掛ける
  ⇒$3×2^6＝192$

　何番目の数でも、初項に公比を掛けることは変わりません。

　では、公比をいくつ掛けるか？　図と照らし合わせながら考えましょう。

　3番目の数を求めるときは公比を2つ掛ける

　5番目の数を求めるときは公比を4つ掛ける

　7番目の数を求めるときは公比を6つ掛ける

『○番目の数よりも1小さい数』だけ公比を掛けるんだね！

　では、『n番目の数』を求めるにはどうしたら良いでしょうか？

　初項$a_{1}$、公差rの数列のn番目の数を求めるには、初項$a_{1}$に、公比rを$n-1$個掛ける。すると式は以下のようになります。

　$a_{n}=a_{1}･r^{n-1}$

　これが等比数列の一般項の公式です。

まとめ

　以上で、等差数列と等比数列の一般項の公式が成り立つ理由を解説しました。

　改めて解説されると『あたりまえじゃん！』と思うような内容だったかと思います。

　このように小学生でも理解できる内容ですので、難しい公式を丸暗記するだけ損です。

　公式の成り立ちを理解し、公式を忘れにくく、忘れたとしても思い出せるようにしましょう。