平方根を用いた二次方程式の解き方を解説【$x^2=○$/$(x\pm \square {)}^2=○$】

　中3になってから特に、数学を難しく感じている人がいるかもしれませんね。

　今回はその苦手意識を少しでも軽くするために、平方根を用いて解く二次方程式『$x^2=○$』と『$(x\pm \square {)}^2=○$』の解き方を、分かりやすく説明します。

　この記事では具体的な解き方を解説する前に、二次方程式を解くときのの基本的な考え方をお話しします。

　考え方がわかれば、二次方程式を解くための操作の目的を理解しやすくなります。

　そのあとで平方根を用いた『$x^2=○$』と『$(x\pm \square {)}^2=○$』の解き方を解説します。

　『$(x\pm \square {)}^2=○$』については、平方完成をするパターンも解説します。

　最後に平方根を用いて解く二次方程式の問題演習を用意しているので、実践力を磨いていってください。

二次方程式を解くときの基本的な考え方

　まずは二次方程式を解く考え方を整理しましょう。

　では、二次方程式『$x^2=○$』『$(x\pm \square {)}^2=○$』を『x=○○』の形にするにはどうすればよいか。

　両辺を2乗される前の数にすれば、『x=○○』になります。

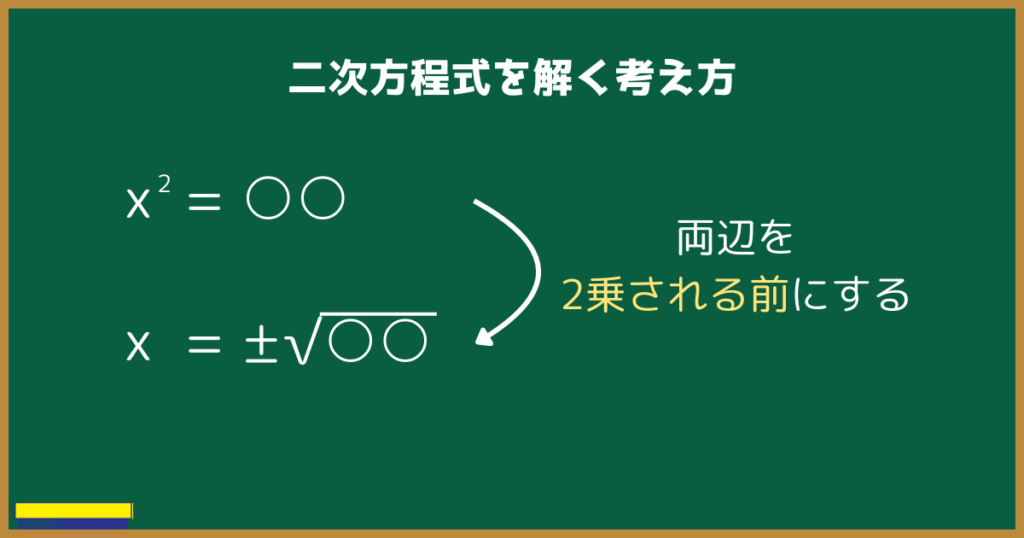
　左辺$x^2$の2乗される前は、当然『$x$』です。

じゃあ右辺の数は、2乗される前はどんな数だったんだろう？

　このように二次方程式を解くために、右辺の2乗される前の数はなんだろう？と考えるのです。

二次方程式『$x^2=○$』『$(x\pm \square {)}^2=○$』の解き方

　ここからは平方根を用いた二次方程式の解き方を3パターン解説します。

それぞれについて、以下で詳しく解説します。

①$x^2=○$の解き方

　まずは①について。

　$x^2=4$を解くには、両辺を2乗される前の数にします。

　左辺$x^2$の2乗される前は$x$

　では、4の2乗される前はなんでしょうか？

4が2乗される前は『2』だね！

　2乗される前の数は正の数だけではありません！

　よって、4の、2乗される前の数は『2と-2』です。

　次は②について。

　①と同じように、両辺を2乗される前に戻しましょう。

右辺『7』の2乗される前の数ってなんだろう？

　7は4のように、2乗される前の数を整数で表すことはできません。

　こういうときはルートを用いて答えます。

　ルートを用いて表すときも、プラスとマイナスの両方があるのがポイントです。

②$(x\pm \square {)}^2=○$の解き方

　まずは①について。

　左辺が$(x+2{)}^2$と式になっていますが、両辺を2乗される前に戻すという考え方は同じです。

左辺$(x+2{)}^2$の2乗される前は$x+2$

また、右辺9の2乗される前の数は±3だね。

　よって式は以下のようになります。

　$(x+2{)}^2=9$

　$x+2=\pm 3$

　$x=-2\pm 3$

　計算はこれで終わりではありません。

　$x=-2\pm 3$は、$-2+3$と$-2-3$の2つを表しています。

　したがって、$x$の値を求めるためには$-2+3$と$-2-3$の計算をします。

　次は②について。

　①と同じように、両辺を2乗される前に戻しましょう。

　$(x-3{)}^2=5$

　$x-3=\pm \sqrt{5}$

　$x=3\pm \sqrt{5}$

　最後に『-3』を移項したら終わりです。

整数とルートの数は計算できないもんね

③【発展】平方完成を用いた$(x\pm \square {)}^2=○$の解き方

　ここからは発展編、平方完成を用いた$(x\pm \square {)}^2=○$の解き方を解説します。

　問題の式『$x^2+4x=7$』を②$(x\pm \square {)}^2=○$の解き方で解くために、一手間を加えて因数分解できるようにします。

　その一手間こそが、平方完成です。

　問題の式『$x^2+4x=7$』の左辺って、ちょっと惜しいですよね。

もし左辺が『$x^2+4x+4$』だったら、

『$(x+2{)}^2$』に因数分解できるのに

　それなら左辺に4を足してしまいましょう！

勝手に数字を足しちゃっていいの？

　もちろん、数字を足しただけだと問題が変ってしまうのでダメです。

　4を足したら、同時に4を引くのです。

　そして、足した4だけを使って因数分解します。

　あとは②$(x\pm \square {)}^2=○$の解き方と同じです。

　平方完成についてもっと詳しく知りたい人は、以下の記事も参考にしてくださいね。

【問題演習】二次方程式『$x^2=○$』『$(x\pm \square {)}^2=○$』

　これまでで習ったことを活かして、問題演習を行いましょう。

　以下、解答です。

①$x^2=25$

　両辺を2乗される前に戻します。

　$x^2=25$

　$x=\pm 5$

　5だけでなく『-5』も忘れずに！

②$(x+3{)}^2=16$

　②について。

　両辺を2乗される前に戻します。

　$(x+3{)}^2$の2乗される前は$x+3$ですよね。

　$(x+3{)}^2=16$

　$x+3=\pm 4$

　$x=-3\pm 4$

　ここまで来たら、$-3+4$と$-3-4$を計算し、答えとします。

　$x=-3\pm 4$

　$x=1,-7$

③$(x-1{)}^2=18$

　②と同じように、両辺を2乗される前に戻します。

　$(x-1{)}^2=18$

　$x-1=\pm \sqrt{18}$

　$x=1\pm 3\sqrt{2}$

　整数とルートの数は計算できないので、これで終わりです。

　また、$\sqrt{18}$は忘れずに$3\sqrt{2}$に変形しましょう。

④$x^2-8x=6$

　$x^2-8x=6$を解くには、平方完成をします。

　平方完成をすることで右辺を$(x\pm \square {)}^2$の形にし、平方根を用いて二次方程式を解きます。

　平方完成をするには、$(x\pm \square {)}^2$の形に因数分解するために、ある数を足して、引くのでした。

$x^2-8x$には、16を足したら$(x\pm \square {)}^2$の形に因数分解できるね

　右辺を、16を足して引く式にすれば、$(x\pm \square {)}^2$の形に因数分解できます。

まとめ

　二次方程式『$x^2=○$』『$(x\pm \square {)}^2=○$』の解き方についてまとめます。

　これらの解説と練習問題を通じて、二次方程式の解き方に自信を持つことができるようになります。

　今後も学校の教科書や問題集なども使って問題演習を重ねていきましょう！