【中3数学】円周角の定理のポイント3選+1！基礎知識と基礎問題を丁寧に解説

　円周角を求める問いは、高校入試で頻出です。

　しかし円周角の定理を使いこなせずに、模試や過去問で正解できずに困っている人がいることでしょう。

　この記事では、円周角の問題を解くために必須な知識を3つにまとめて解説します。

　その後で問題演習を行い、知識の定着を図ります。

　また、都立高校入試でよく問われる知識も確認するので、ぜひそれも見てみてください。

円周角の定理のポイント3選+1

　まずは円周角を求める問いで、ポイントとなる知識を3つ解説します。

　その後で、都立高校入試でよく問われる知識も解説します。

①円周角は中心角の半分

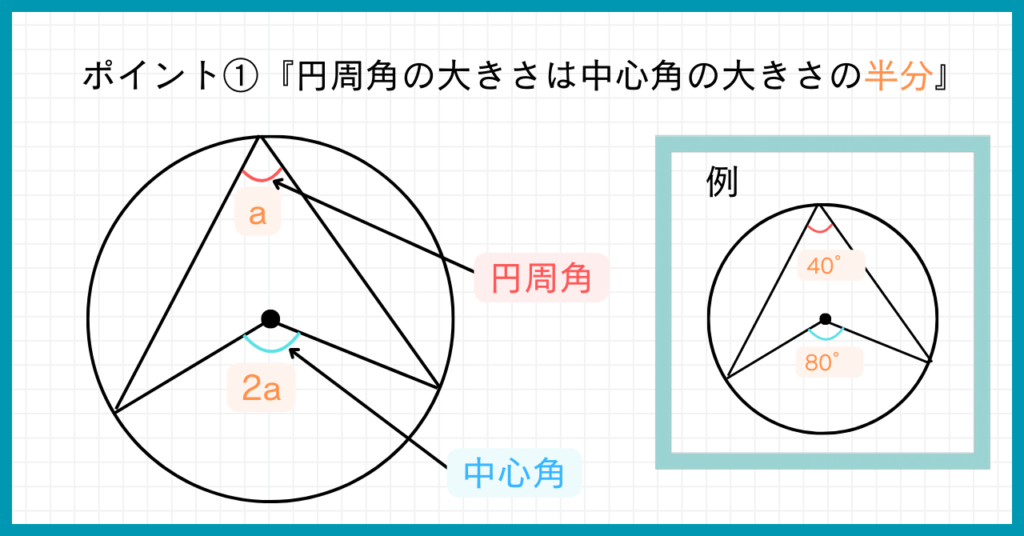
　まずは基礎中の基礎『円周角の大きさは中心角の大きさ半分』です。

　例えば中心角が80°であれば、円周角は40°です。

②直径に対する円周角は90°

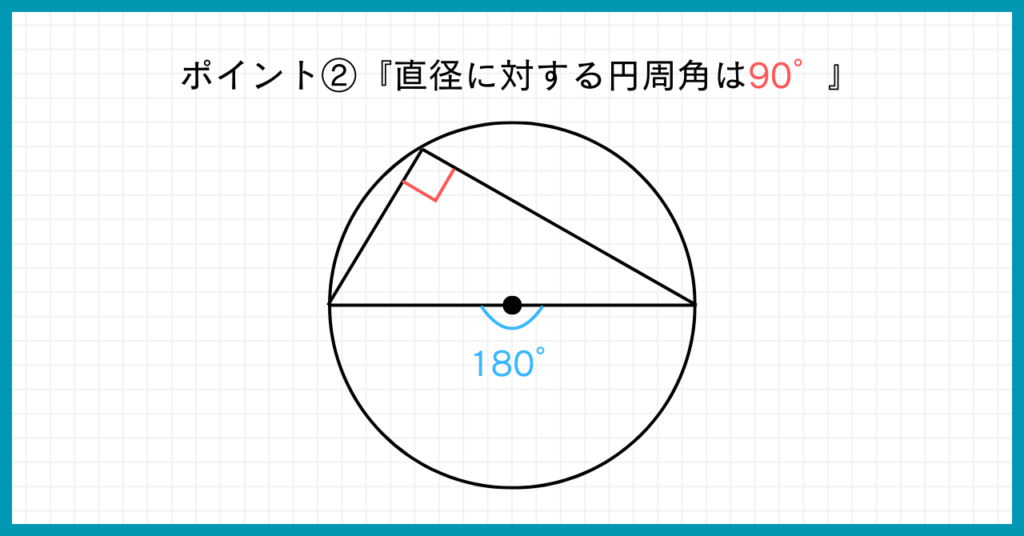
　円周角の大きさは中心角の大きさの半分であれば、中心角が180°の時の円周角、つまり直径に対する円周角は何°でしょうか？

円周角は中心角の半分なんだから、中心角が180°なら円周角は90°だね！

③同じ弧や同じ長さの弧に対する円周角は等しい

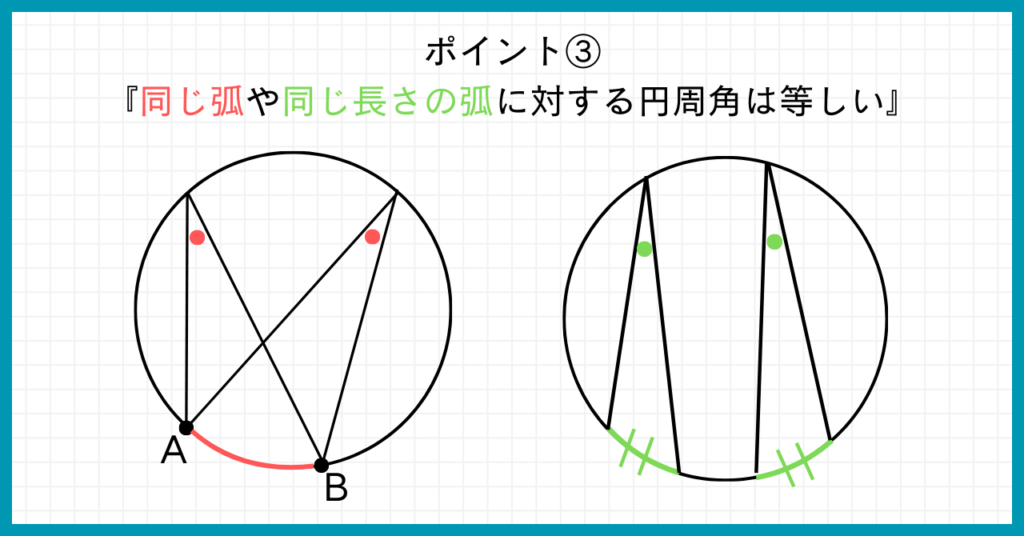
　これまでは円周角と中心角の関係を見てきました。

　ここからは円周角と弧の関係を見ていきましょう。

　同じ弧に対する円周角は等しくなります。

　また弧の長さが等しいなら、円周角も等しいです。

【都立高校入試】円周角の大きさは弧の長さに比例する

　ポイント③で、同じ弧、また弧の長さが等しいなら円周角の大きさも等しいとお話しました。

　では、弧の長さが2倍、3倍……と大きくなったら、円周角の大きさはどうなるでしょうか？

　そう、円周角の大きさも2倍、3倍……となります。

つまり、円周角の大きさは弧の長さに比例します

　この知識を用いて角度を求める問いが最近、都立高校入試の大問1で出題されています。(2024年11月現在)

　大問1は得点源になるので、都立高校入試を受験する人は必ず覚えておいてくださいね。

　もっと詳しく知りたい人は、以下の記事も読んでくださいね。

【問題演習】円周角の大きさを求める

　ここからは、今まで習ったポイントを用いて円周角を求める問題を行いましょう。

問題

次の角度xを求めなさい。

ただし、③において中心を通る直線はその円の直径である。

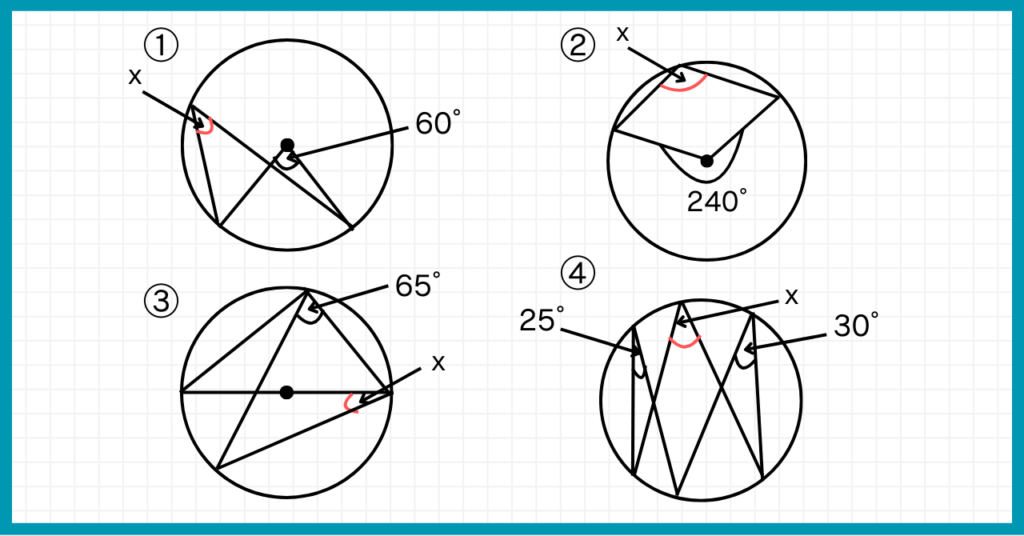
①円周上を移動させる

　初めて円周角の問題を解く人は、一瞬戸惑ってしまうかもしれませんね。

　しかしポイント③より同じ弧に対する円周角は等しいので、下図のように円周角を移動できます。

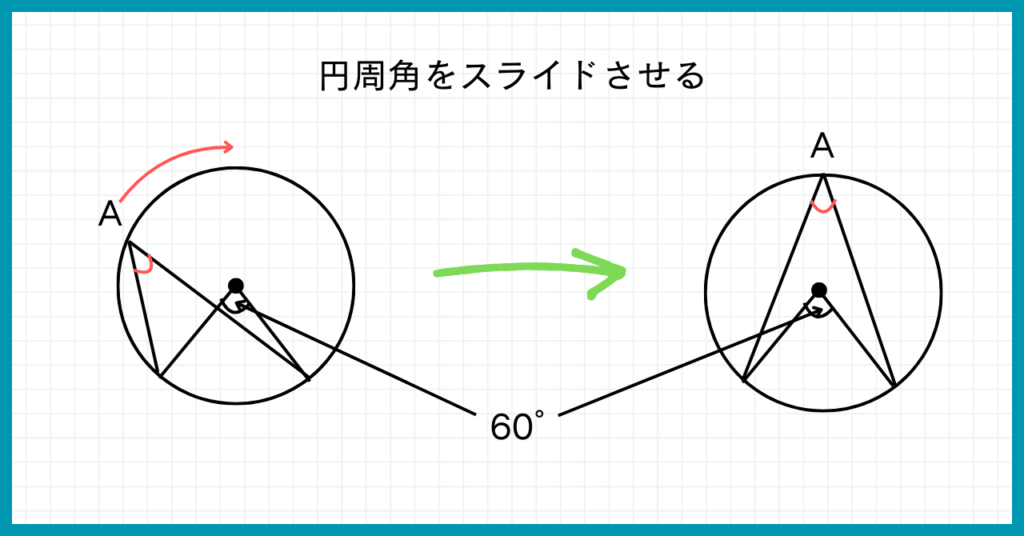
　よって円周角は中心角の半分なので、60÷2=30よりx=30°

②中心角が180°以上

四角形みたいなのがある！

こういうときはどうすればいいんだろう？

　このタイプの問いで戸惑ってしまう人がいるかと思いますが、解き方は変りません。

　この図形では中心角が240°なので、円周角はその半分でx=120°です。

③直径に対する円周角を利用

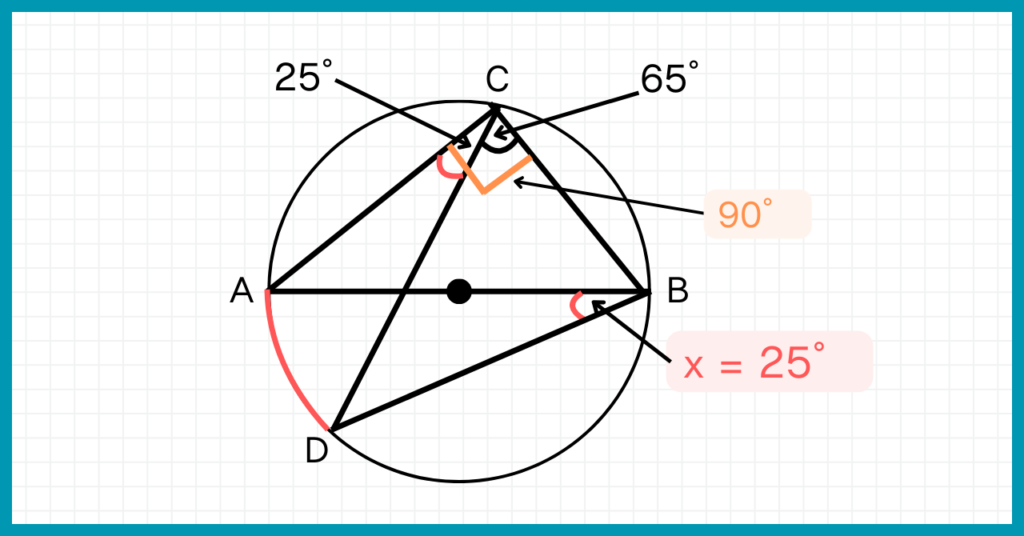
　直径に対する円周角に気づいたでしょうか。

　直径に対する円周角∠ACBが90°なので、∠ACB=90-65=25°ですね。

　さて、円周角の定理より∠ACB＝∠ABD=25°なので、x=25°

④補助線を引く

　この問いは、図をじーっと眺めているだけでは解けません！

　円周角の定理を使うために、補助線を引きましょう。

　EBに補助線を引くと、∠ADB＝∠AEB、∠BEC＝∠BFCであるとわかります。

　よってx=25+30=55°

まとめ

　今まで図形は得意だったという人でも、円周角の定理を使いこなすのに苦労することがあるでしょう。

　相似の証明でも円周角の定理が根拠になることがあります。

　相似の証明といえば、入試で頻出の問いですよね。

　志望校に合格するためにも、円周角の定理をきちんと使いこなせるようにしていきましょう。