【図解】円錐の表面積の求め方をわかりやすく！裏技も紹介

　空間図形の体積や表面積を求める問題の中で、一番難しいのは円錐の表面積を求める問題でしょう。

　問題集の解説を読んでみてもよくわからない！　という人が多いのではないでしょうか。

　円錐の表面積を求めるには、円錐の展開図やおうぎ形の面積を求める公式といった前提知識が必要です。さらに、それらを使いこなせないと解くことができないのです。

　この記事では円錐の表面積の求め方を、前提知識からわかりやすく解説します。

　さらに円錐の表面積の求め方の裏技も紹介します。

　この記事を読めば円錐の表面積を求めるポイントがわかり、さらに裏技を覚えて周りと差を付けられますよ！

円錐の表面積を求めるのに必要な知識3選

　円錐の表面積を求めるには以下の前提知識が必要です。

　ドキッとするものがあったら、以下の解説を読んでください。

①円錐の展開図

　円錐の展開図はイメージできますか？

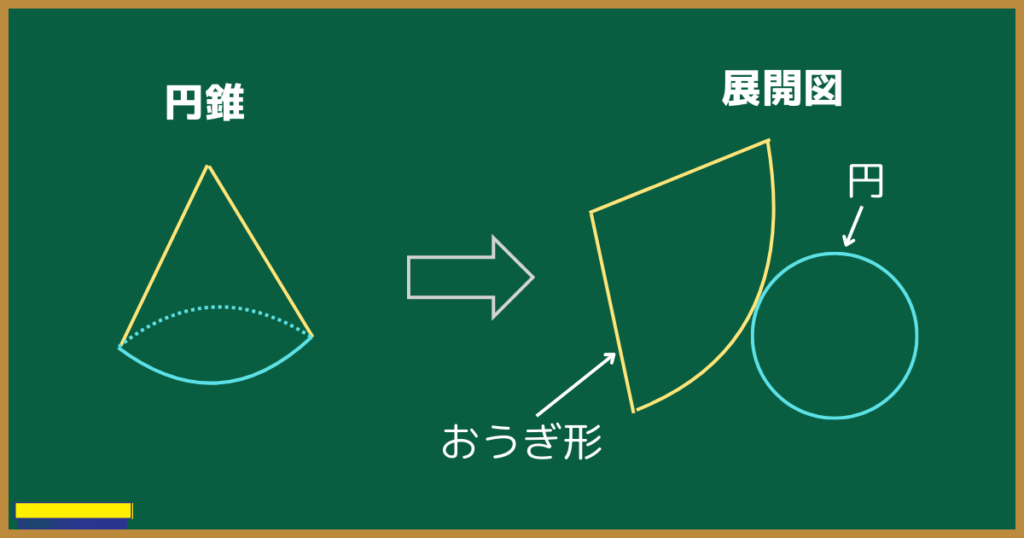
　このように、円錐の展開図は円の部分とおうぎ形の部分に分かれます。

②円の面積を求める公式

　円の面積を求める公式は大丈夫ですか？

　お馴染みの『半径×半径×円周率』を文字で表したものです。

　半径はrで、円周率はπなので、

　$半径×半径×円周率＝r×r×π＝πr^2$

　となるのです。

③おうぎ形の面積を求める公式と弧の長さを求める公式

　おうぎ形の面積を求める公式は以下です。

　おうぎ形の面積を求める公式の$πr^2$の部分が、円の面積と似ていますね。

　また、弧の長さを求める公式の$2πr$

　その理由は以下の記事に書いてあります。

円錐の表面積の王道の求め方と裏技を解説

　ここからは円錐の表面積の求め方を2パターン紹介します。

　初めは中学校で習う王道の求め方を解説します。

　次に公式を使った裏技を紹介します。

　裏技の方が解き方としてはラクですが、公式を忘れてしまったら解けません。

　テストで忘れてしまったら大変なので、裏技だけ読むのではなく王道の求め方から理解してくださいね。

【王道の求め方】側面の中心角aを求める

例題

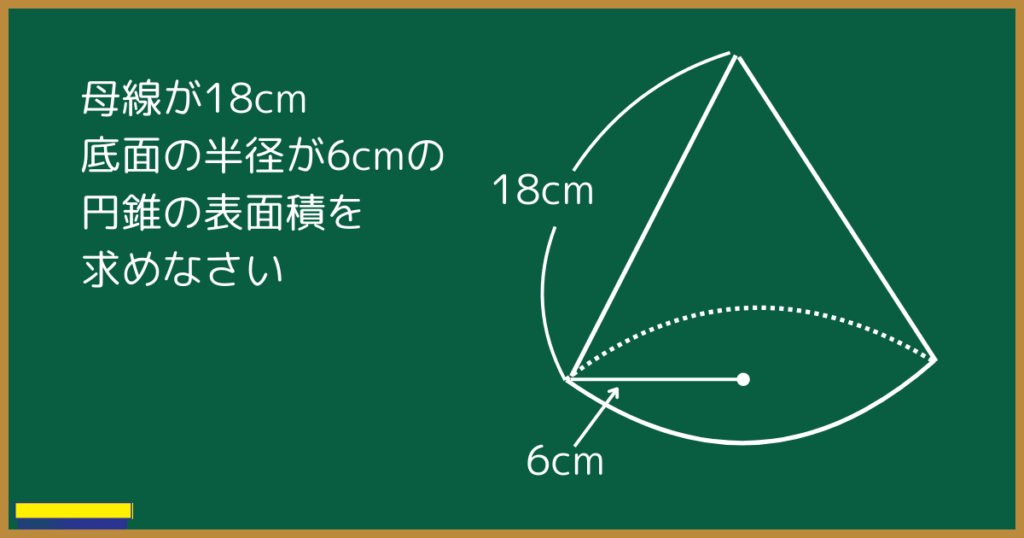
　円錐の表面積を求める手順は以下です。

①展開図を描く(慣れたら省略OK)

　角錐とは違って、円錐は側面積を求めるイメージがつきづらいですよね。

　そこで、円錐の展開図を描いてみましょう。

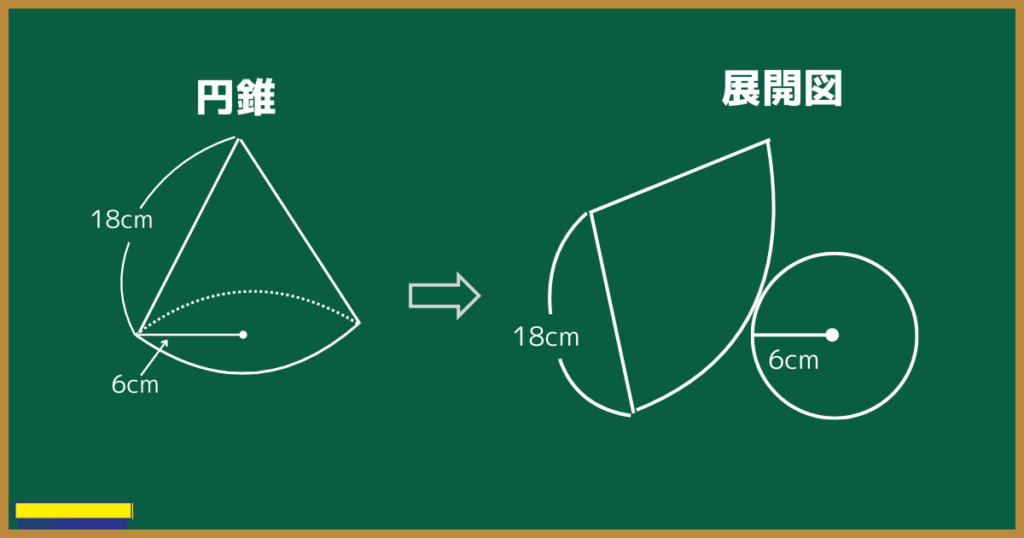
　このように、円錐は円とおうぎ形でできているので、それぞれの面積を求めて足せば、円錐の表面積を求められます。

②側面のおうぎ形の中心角aを求める

　円の面積は問題ないでしょう。

　難しいのは、おうぎ形の面積を求めることです。

　おうぎ形の面積を求める公式は以下です。

　$S=πr^2×\frac{a}{360}$

半径は問題に書いてあるけど、中心角がわからない！

　つまり、おうぎ形の面積を求めるためには、おうぎ形の中心角aを求める必要があります。

　その中心角を求めるため、おうぎ形の弧の長さを求める公式を用います。

　$弧の長さl=2πr×\frac{a}{360}$

　実は問題文の条件から、おうぎ形の弧の長さを求められます。

　半径も13cmとわかっていますから、半径と弧の長さを公式に代入すれば、一次方程式のようにaを求められます。

　まず、おうぎ形の弧の長さを求めましょう。

　おうぎ形の弧の長さは、円周の長さと同じです。

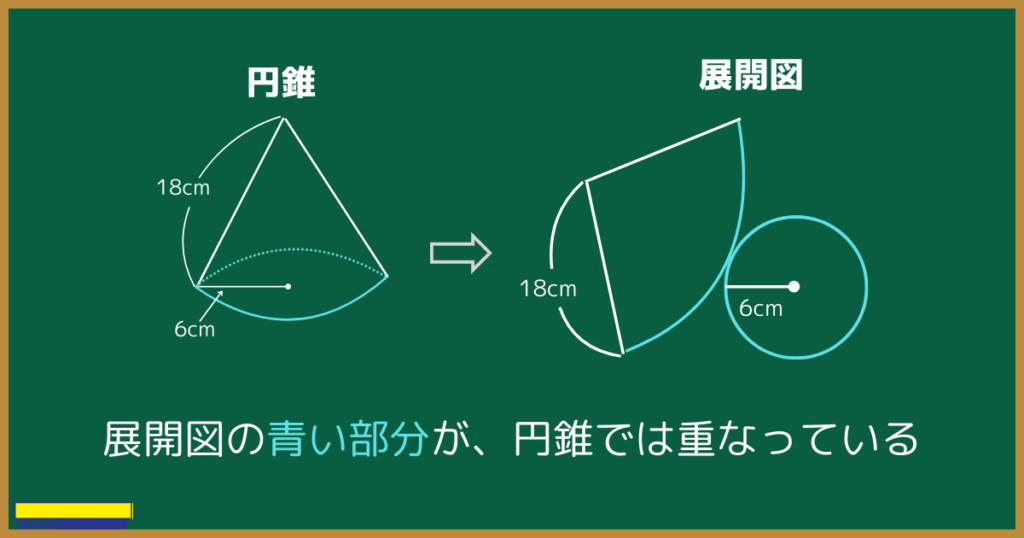
　つまりおうぎ形の弧の長さは、円周の長さ$\color{red}{2πr=2×π×6=12πcm}$です。

　この$12π$とおうぎ形の半径18cmを、おうぎ形の弧の長さを求める公式に当てはめ、中心角aを求めます。

　$弧の長さl=2πr×\frac{a}{360}$より

　$12π=2π×18×\frac{a}{360}$

　$12π×360=36π×a$

　$a=120$

　このようにして、おうぎ形の中心角の大きさがわかりました。

③おうぎ形の面積を求め、円の面積と足す

　円錐の表面積は(おうぎ形の面積)+(円の面積)で求められます。

　おうぎ形の面積は②で求めた中心角a=120°と、半径18cmを用いて求めます。

　また円の面積は、円の半径6cmを用います。

　円錐の表面積をSとする。

　(円錐の表面積)=(おうぎ形の面積)+(円の面積)なので

　$S=18^2×π×\frac{120}{360}+6^2×π$

　$S=324π×\frac{1}{3}+36π$

　$S=108π+36π$

　$S=144π$

　よって円錐の表面積は$\color{red}{144π}(cm^2)$

【裏技】円錐の側面積を求める公式

　円錐の表面積を求める問いで難しいのは、円錐の側面積を求めるため、おうぎ形の中心角を求めなければならないことです。

　実は、面倒な計算をしなくても一発で円錐の側面積を求める公式があるのです。

円錐の側面積を求める公式

円錐の側面積をS、母線を$l$、底面の半径をrとする。

$S=πlr$

　この公式は円錐の表面積のおうぎ形に使える公式です。

　普通のおうぎ形の面積を求める時には使えないので注意です。

　この公式を使って、さっきと同じ例題を解いてみましょう。

例題

　円錐の表面積は$S=πlr$で求められます。

　母線$l$=18cm、底面積の半径r=6cmなので、公式に当てはめると以下のようになります。

　$S=π×18×6$

　$S=108π$

　以上より側面積は$108π(cm^2)$です。

　底面の円の面積は$6^2π=36π$ですね。

　よって円錐の表面積は$108π+36π={\color{red}{144π(cm^2)}}$

　側面の中心角aを求める方法と答えが一致しましたね。

公式を使った方がラクじゃん！

　確かにこの裏技を知っていれば圧倒的に早く解けます。

　しかし公式を新たに覚えなければならないので、公式を忘れるリスクがあります。

　また、側面の中心角を求める方法で用いる『底面の円周と側面のおうぎ形の弧の長さが一致するという考え方』は、今後色々な問題で使います。

　裏技を使うのは、側面の中心角を求める方法を理解した上でお願いしますね。

まとめ

　円錐の側面積の求め方についてまとめます。

　表面積を求める問題は計算が複雑になるのでミスしやすいです。

　特に円錐の表面積を求める問いは中心角を求める必要があるので、計算過程が多くよりミスをしやすいです。

　公式を覚えてさえいれば簡単に計算できるのでミスを防げますが、肝心の公式を忘れてしまっては解答できないので、面倒でも王道の解法をしっかり理解してくださいね。