【例題でわかる】反比例の変化の割合は公式で求める!その方法を解説

一次関数の変化の割合を習ったあと、応用問題と称して『反比例の変化の割合』を問われることがあります。

反比例の変化の割合なんて習ってないよ?
実は反比例の変化の割合を求めるには、一次関数の変化の割合の公式を用いればよいのです。
しかし、一次関数のときにやったような、『y=2x+1だから変化の割合は2』という一発でわかる方法はありません。
なぜなら、反比例の変化の割合は一次関数と違って一定ではないからです。
この記事では反比例の変化の割合を求める方法を解説したあと、反比例の変化の割合が一定ではない理由を解説します。
反比例の変化の割合を求める方法
反比例の変化の割合を求める方法は一次関数と同じです。
まずは一次関数の変化の割合を求める公式を確認しましょう。
その後で、例題を用いて反比例の変化の割合を求める方法を解説します。
変化の割合を求める公式は一次関数と同じ
一次関数の変化の割合を求める公式は覚えていますか?
反比例の変化の割合を求めるためにも、一次関数で習った変化の割合の公式が使えます。
忘れてしまった人は、今から覚えましょう。

yの増加量? xの増加量?
なんだっけ?
変化の割合の公式がよくわからない人は、以下の記事を読んでくださいね。
【例題】反比例の変化の割合を求める方法
反比例の変化の割合を求める問いをやってみましょう。
例題
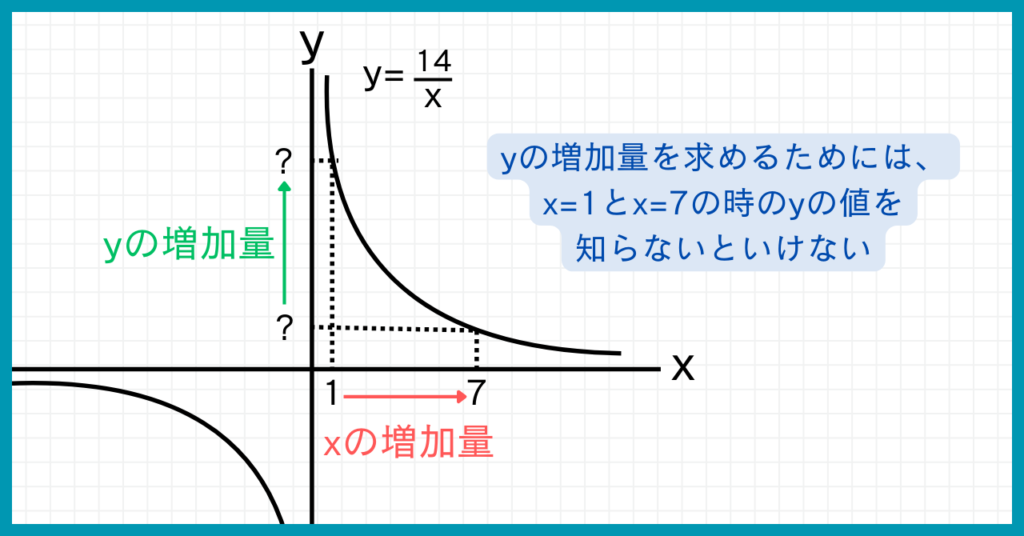
$y=\frac{14}{x}$で、xが1から7まで増加するときの変化の割合を求めよ。
一次関数のときに習った変化の割合の公式に当てはめて考えましょう。
さて、変化の割合の公式を使うためには、xの増加量とyの増加量が必要です。

xの増加量は『xが1から7まで増加する』ことから求められるね
yの増加量を求めるためには、x=1とx=7の時のyの値を知らないといけませんね。
x=1のとき、$y=\frac{14}{x}$より
$y=\frac{14}{1}=14$
また、x=7のとき、$y=\frac{14}{x}$より
$y=\frac{14}{7}=2$
よって$(変化の割合)=\frac{(yの増加量)}{(xの増加量)}$より、xが1から7まで増加するときの変化の割合は
$\frac{(yの増加量)}{(xの増加量)}$
$=\frac{2-14}{7-1}$
$=\color{red}{-2}$
反比例の変化の割合は一定じゃない!その理由は?
一次関数の変化の割合なら、例えば$y=3x-1$なら変化の割合は3と一発でわかりましたよね。

反比例の変化の割合は、一次関数みたいに一発ではわからないの?
反比例の変化の割合は、残念ながら式を見ただけではわかりません。
なぜなら反比例は、一次関数とは違って変化の割合が一定ではないからです。
以下で詳しく解説します。
そもそも変化の割合とは何か?
そもそも変化の割合とは何かを、今一度確認しましょう。
つまり変化の割合の公式は、xが1増えるごとにyの値がどれだけ増えるのかを求めるためにあるのです。

だから
$(変化の割合)=\frac{(yの増加量)}{(xの増加量)}$で、
yの増加量をxの増加量で割るんだね。
一次関数は変化の割合つまりxの増加量1あたりのyの増加量が一定で、それが$y=ax+b$のaにあたるのです。
しかし反比例は、xの増加量1あたりのyの増加量が一定ではないのです。
次の段落では、反比例の変化の割合と一次関数の変化の割合の違いを、図を用いて見比べていきます。
【図解】反比例の変化の割合を一次関数の変化の割合と比べてみよう
前の段落で、変化の割合とはxの増加量1あたりのyの増加量であるとお話しましたね。
この段落では一次関数の変化の割合は一定なのに対し、反比例の変化の割合は一定ではないことを、図で確認していきましょう。。
まずは一次関数の変化の割合を見ていきましょう。
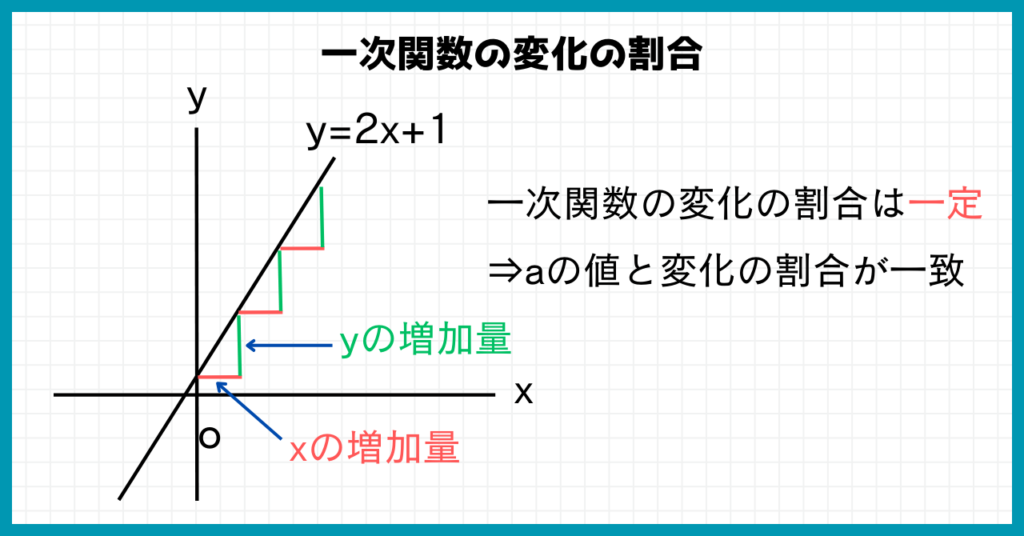
一次関数の変化の割合を図で見てみると、階段のように一定ですよね。
この一定になっている変化の割合が、一次関数の式$y=ax+b$のaにあたります。
だから、一次関数の変化の割合は式を見ただけで一発でわかるんですね。
対して、反比例の変化の割合はどうでしょう。
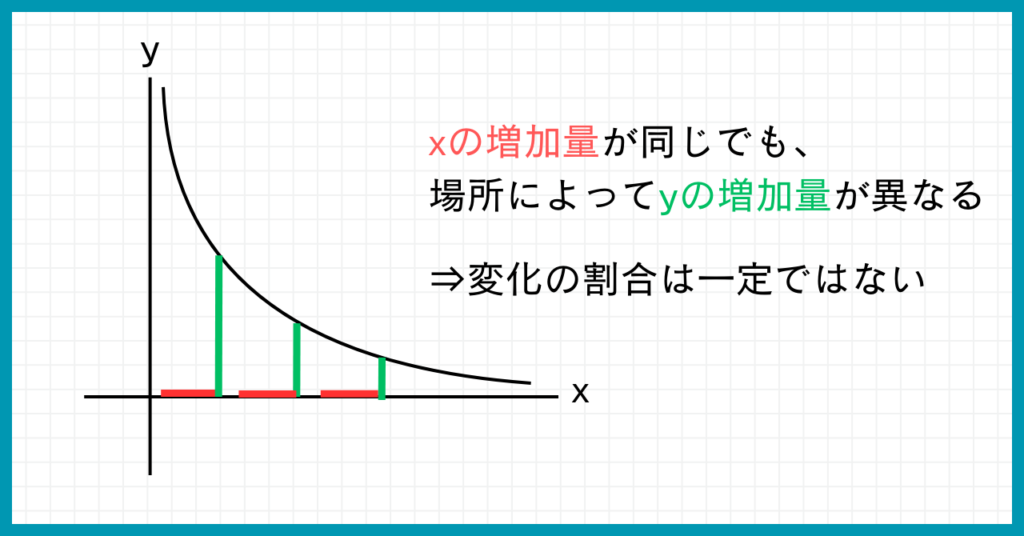
一次関数の変化の割合は、図で表すと階段のように一定になりました。
しかし反比例の変化の割合は、図で表すと幅が一定ではないですよね。

この図みたいな階段だったら転んじゃうね!
このように反比例の変化の割合は一定ではない、つまりxの増加量をどこからどこまでとったかによりyの増加量が変わってしまいます。
よって、反比例の変化の割合は、式を見ただけではわからないのです。
まとめ
反比例の変化の割合を求める問いが出てきて、こんなの習ってない!と思った人がいるかもしれません。
しかし変化の割合の意味がわかっていれば、特に習っていなくても反比例の変化の割合を求められるはずです。
一次関数の変化の割合は求められても反比例の変化の割合が求められなかった人は、数学で出てくる用語の意味をしっかり理解するようにしてくださいね。

コメントを残す