【中3相似】平行線と比の応用問題の解き方を図を用いて丁寧に解説！【縦の長さ・台形】

　相似の単元で出てくる計算問題『平行線と比』は、基本的な問題なら楽勝！　という人が多いかもしれません。

　しかし応用問題になった途端、どの三角形を見て比を取ればよいのかわからなくて問題が解けない！　なんてことがあるかと思います。

　この記事では、平行線と比の公式を用いて線分の長さを求める応用問題を扱います。

　問題の解説に入る前に基本事項を確認するので、不安な人は初めから読んでくださいね。

【基本】平行線と比の公式

　応用問題を行う前に、平行線と比の公式を確認しましょう。

平行線と比の公式①

　公式を見てもピンとこない人は、以下の記事で公式を詳しく解説しているので、先に読んできてくださいね。

【解説】平行線と比の公式の応用問題

　ここからは、平行線と比の公式を用いて線分の長さを求める応用問題を行います。

　先に問題を示すので、解説を知りたい問題から見てくださいね。

問題

次の図形のEFの長さを求めなさい。

ただし、①はAB=8cm、DC=6cmで、AB//EF// DC

②は四角形ABCDが台形、AD=10cm、BC=15cm、さらにAD//EF// BCである。

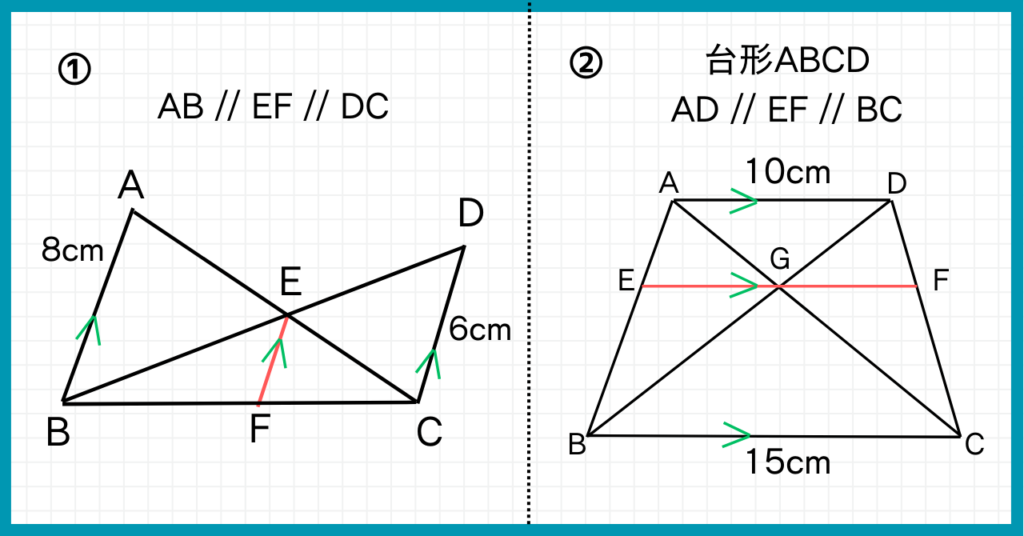
①縦の長さを求める

　まずは①について解説します。

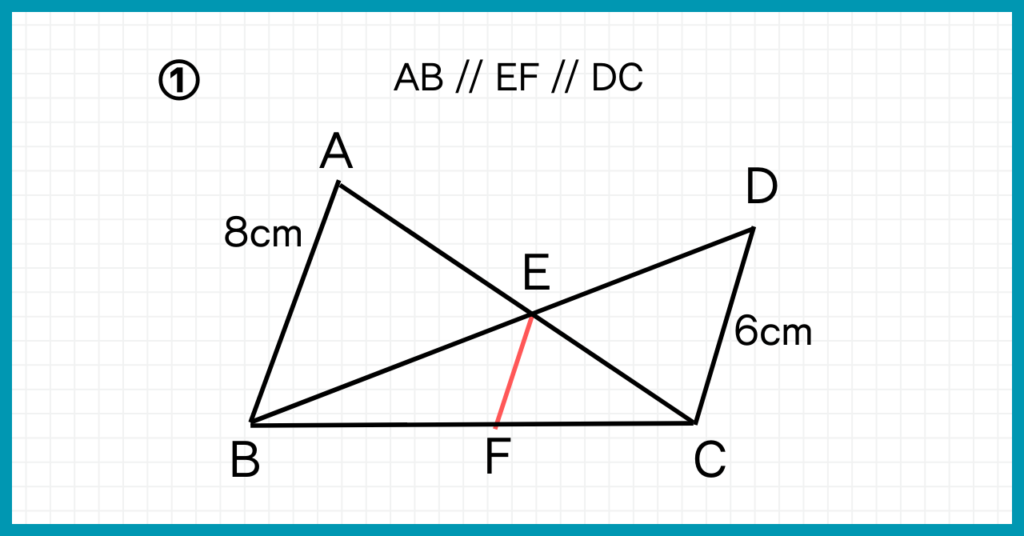
　①のようなタイプの問題を解くポイントは以下です。

　EFの長さを問われているので、EFが関係する三角形を含む相似な三角形を見つけましょう。

それなら、△ABC∽△EFCだね！

EFの対応する辺がABで、ABの長さがわかってるからEFを求められそう！

でも△ABCと△EFCの相似比がわからないから、計算でEFを求められないよ

　そこで、もう一組の相似な三角形を見つけましょう。

もう一つは、△ABE∽△CDE！

AB=8cm、DC=6cmと、対応する辺の長さがわかるから相似比もわかるね！

　AB=8cm、DC=6cmより、△ABEと△CDEの相似比は8:6、つまり4:3です。

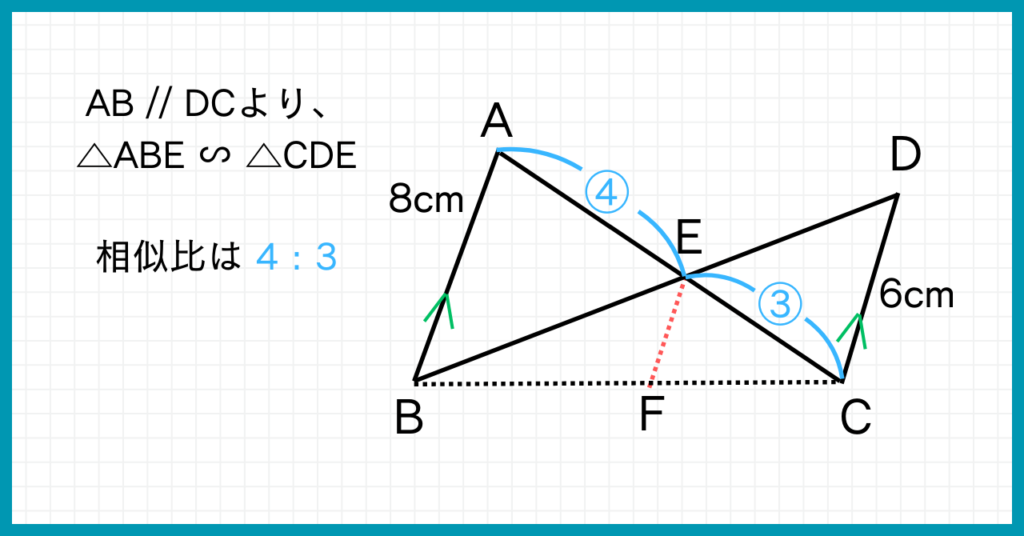
　さて、改めて△ABCと△EFCを見てみましょう。

　△ABEと△CDEの相似比が4:3であることから、AE:EC=4:3であることがわかりましたね。

　このことから、△ABCと△EFCの相似比がわかります！

　△ABCと△EFCの相似比は、AC:ECで求められますよね。

　AC:EC=(AE+EC):ECと見ると、△ABCと△EFCの相似比は(AE+EC):EC=(4+3):3=7:3

　解答をまとめます。

解答①

AB//DCより、△ABE∽△CDE

相似比はAB:DC=8:6=4:3である。

よってAE:EC=4:3

またAB//EFより△ABC∽△EFC

AE:EC=4:3より、AC:EC=7:3なので△ABCと△EFCの相似比は7:3

よってAB:EF=7:3より

8:EF=7:3

$color{red}{EF=\frac{56}{3}}$

②台形の中の長さを求める

　次に②について解説します。

　この問いを解くポイントは以下です。

　問われているのはEFの長さですが、EFを直接求めることはできません。

　EF=EG+FGとみて、EGとFGをそれぞれ求めましょう。

EGを求めるためには△AEG∽△ABC

FGを求めるためには△DGF∽△DBCを用いれば良さそうだね

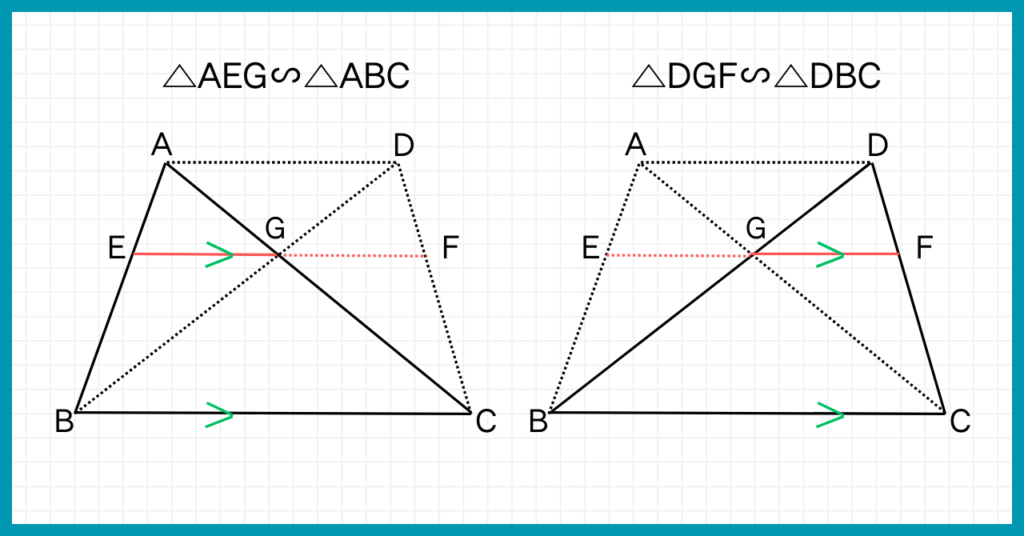
でも相似比がわからないから、EGもFGも求められないよ？

　そこで別の相似な三角形を見つけましょう。

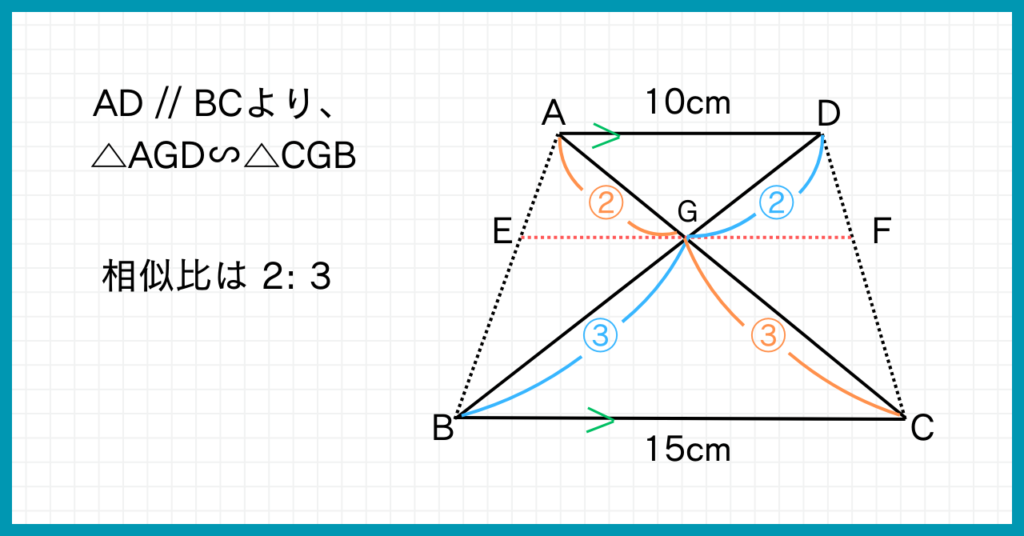
　AD=10cm、BC=15cmとわかっているので、これを利用できないかを考えましょう。

それなら、△AGD∽△CGBが使えそう！

　AD:BC=10:15=2:3

　つまり、△AGDと△CGBの相似比は2:3です。

　さて、改めて『△AEGと△ABC』と、『△DGFと△DBC』を見てみましょう。

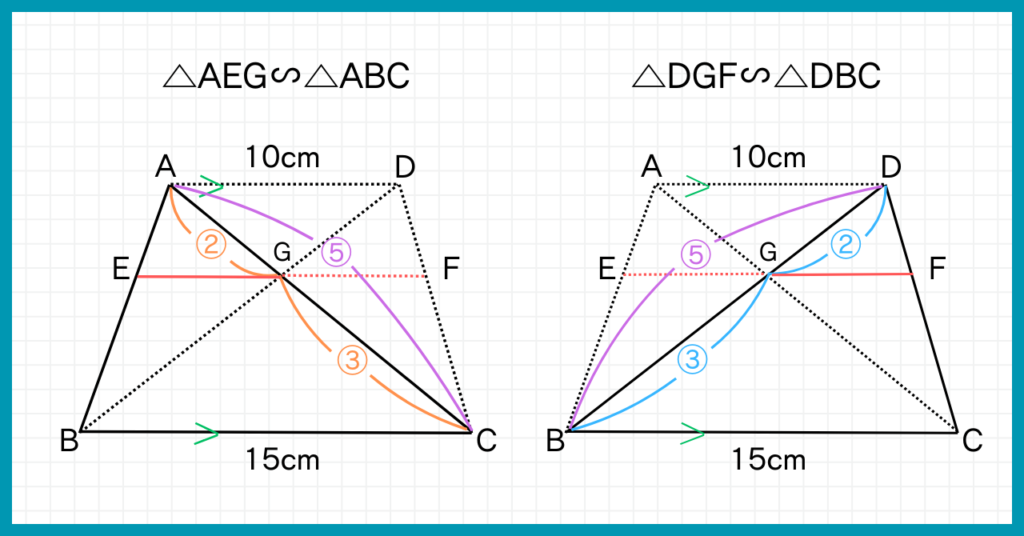
　まず△AEGと△ABCについて。

　AG:GC=2:3より、AG:(AG+GC)=2:(2+3)=2:5

　よって△AEGと△ABCの相似比は2:5です。

　このことから、AG:AC=EG:BCよりEGを求められます。

　次に△DGFと△DBCについて。

　DG:GB=2:3より、DG:(DG+GB)=2:(2+3)=2:5

　よって△DGFと△DBCの相似比は2:5です。

　このことから、DG:DB=FG:DBよりFGを求められます。

　以下で解答をまとめます。

解答②

△AGDと△CGBにおいて、AD//BCより△AGD∽△CGB

AD:BC=10:15=2:3なので、△AGDと△CGBの相似比は2:3

△AEGと△ABCにおいて、EG//BCより△AEG∽△ABC

AG:(AG+GC)=2:(2+3)=2:5なので、△AEGと△ABCの相似比は2:5

よってAG:AC=EG:BCより

2:5=EG:15

EG=6

△DGFと△DBCにおいても同じようにすると

FG=6

よってFG=EG+FGなので

FG=6+6=12

ゆえにFG=12cm

まとめ

　平行線と比の公式を用いる応用問題というだけあって、少し難しかったですよね。

　しかしさまざまな視点から相似な三角形を見つけ、目的の線分の長さを求める過程は問題解決能力を育てるのに役立ちます。

　こんなのなんの役に立つの！　なんて思わずに、平行線と比の公式を用いる応用問題を解けるように問題演習を頑張ってくださいね。