【中2数学】二等辺三角形の性質3つと角度の求め方2パターンを解説

　二等辺三角形の性質は小学校の頃にも習ったけれど、改めて聞かれると答えられない中学生がいることでしょう。

　また、二等辺三角形の角度を求める問題は、二等辺三角形の性質を理解し使いこなせないと難しく感じますよね。

　この記事では二等辺三角形の性質3つを解説したあと、二等辺三角形の角度を求める問題2パターンの解説をします。

　この記事を読めば二等辺三角形の基礎がわかります。

　また、受験によく出る『作図』を解くのに重要な二等辺三角形の性質についても詳しく解説します。

二等辺三角形の性質3つ

　まずは二等辺三角形の性質3つを解説します。

• 2辺の長さが等しい
• 底角の大きさが等しい
• 頂角の二等分線は底辺を垂直に二等分する

①2辺の長さが等しい

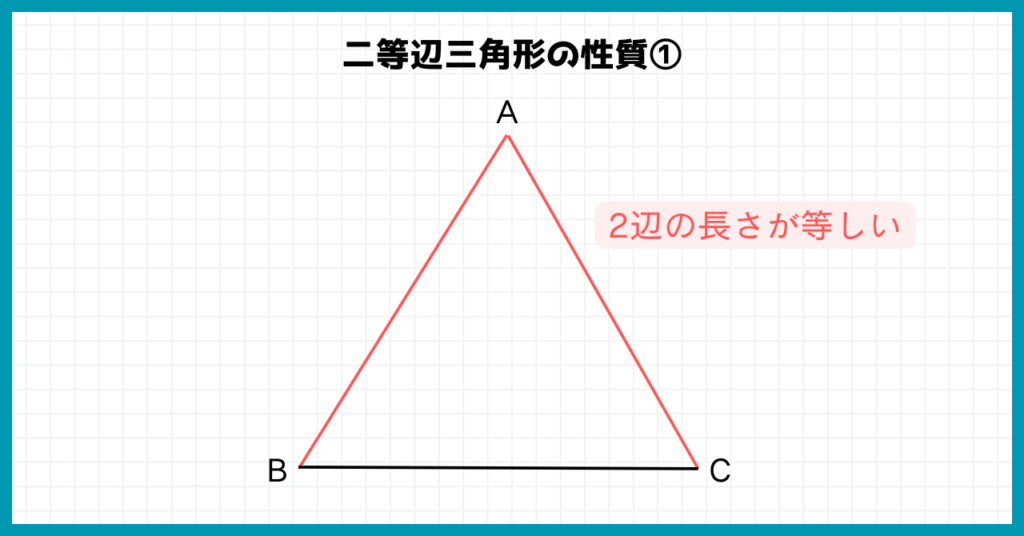
　まずは2辺の長さが等しいことを押さえましょう。

3辺が等しければ『正三角形』。

正三角形は、二等辺三角形の特別な形なのです！

②底角の大きさが等しい

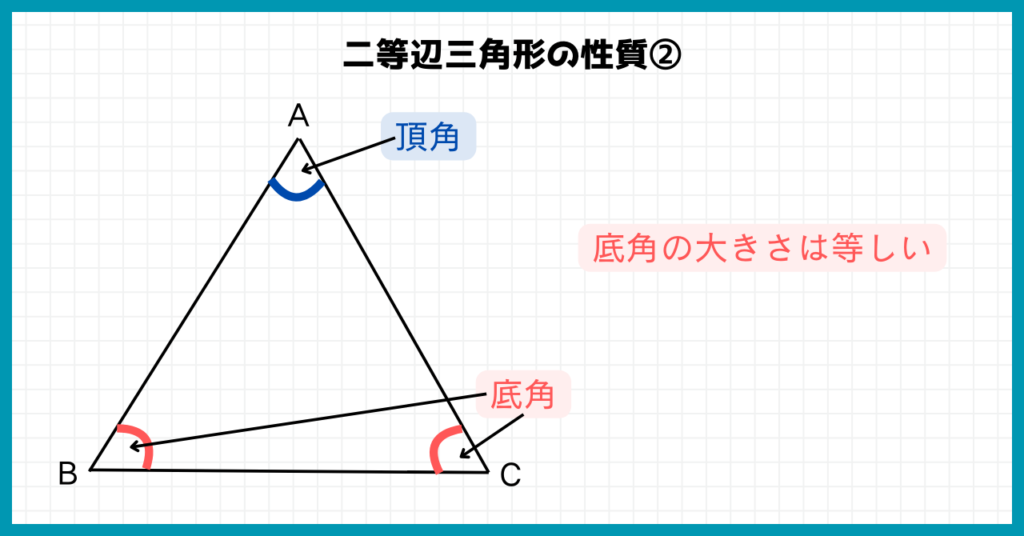
　二等辺三角形の角度を求める問いでは、底角の大きさが等しいことを利用します。

　二等辺三角形の底角ではない角を『頂角』ということも押さえておきましょう。

【受験】③頂角の二等分線は底辺を垂直に二等分する

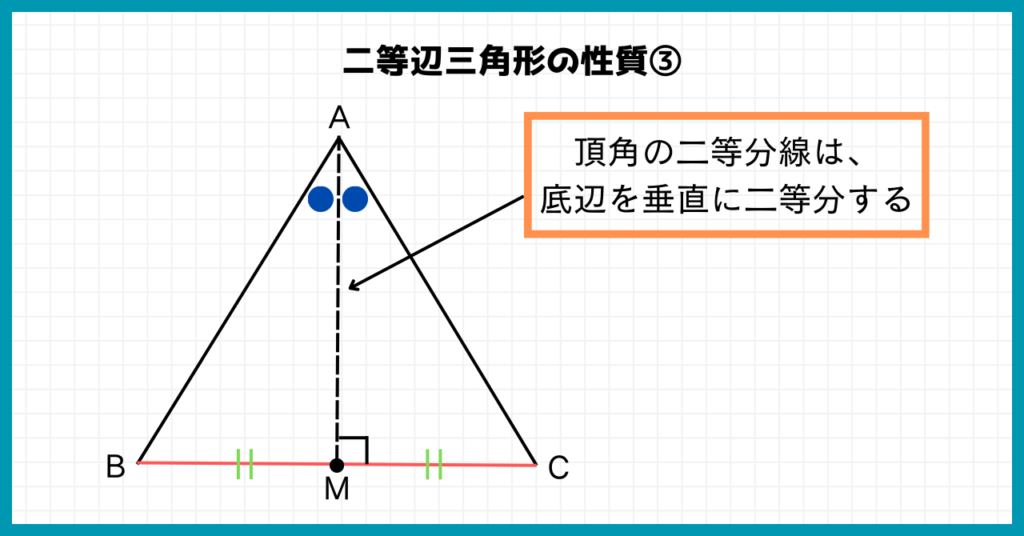
　一番忘れがちなのが『頂角の二等分線は底辺を垂直に二等分する』ことです。

　授業ではあまり使わない性質かもしれませんが、高校入試では作図の問題を解くため重要な基礎知識です。

　『頂角の二等分線は底辺を垂直に二等分する』するなら、逆に『垂直二等分線上の点を結べば、二等辺三角形が出来る』ことも、作図の問題を解くには重要です。

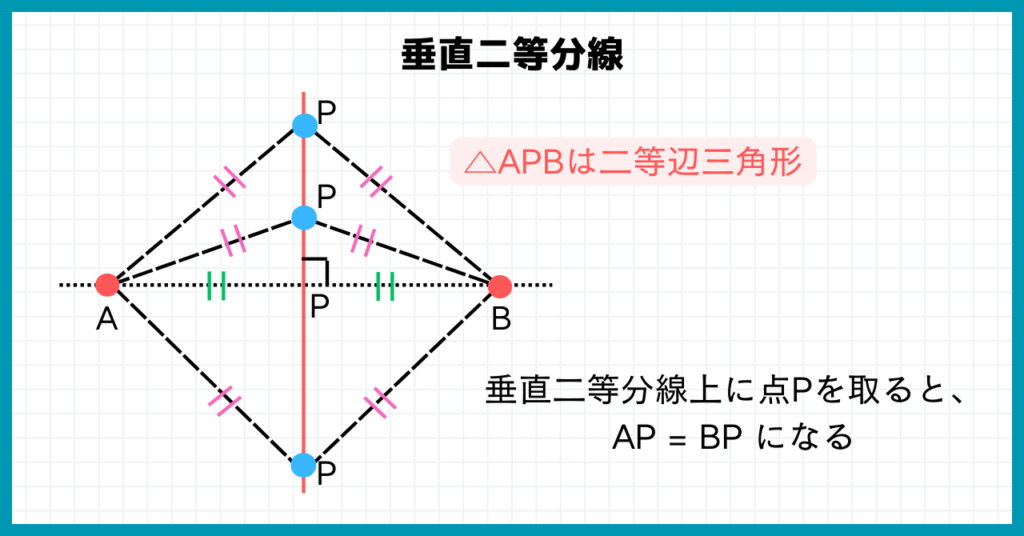
　中1で習った作図『垂直二等分線』を覚えていますか？

　高校入試の作図を解くために、垂直二等分線上の点を結べば二等辺三角形が出来る、つまり上の図で言うとAP=BPになるという性質を用いることがあります。

　この話がピンと来ない人は以下の記事も読んでみてください。

二等辺三角形の角を求める問題

　ここからは二等辺三角形の角を求める問題2パターンをやっていきましょう。

• 頂角が与えられる
• 底角の片方が与えられる

　以下、問題です。

①頂角が与えられる

例題①

xの角度を求めなさい。

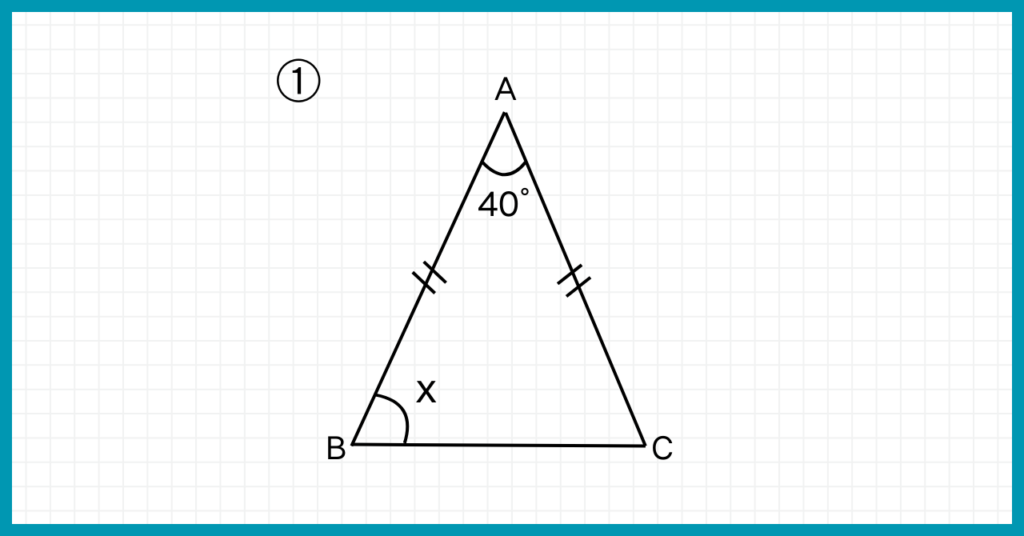
角度が1個しかわからない！

　ここで用いる性質が『②底角の大きさが等しい』です。

　頂角が40°と与えられているので、まずは180-40＝140です。

　残りの140°とはつまり、2つの底角の合計ですね。

　底角の大きさは等しいので、xの角度を求めるには$140×\frac{1}{2}$をすれば良いのです。

②底角の片方が与えられる

例題②

xの角度を求めなさい。

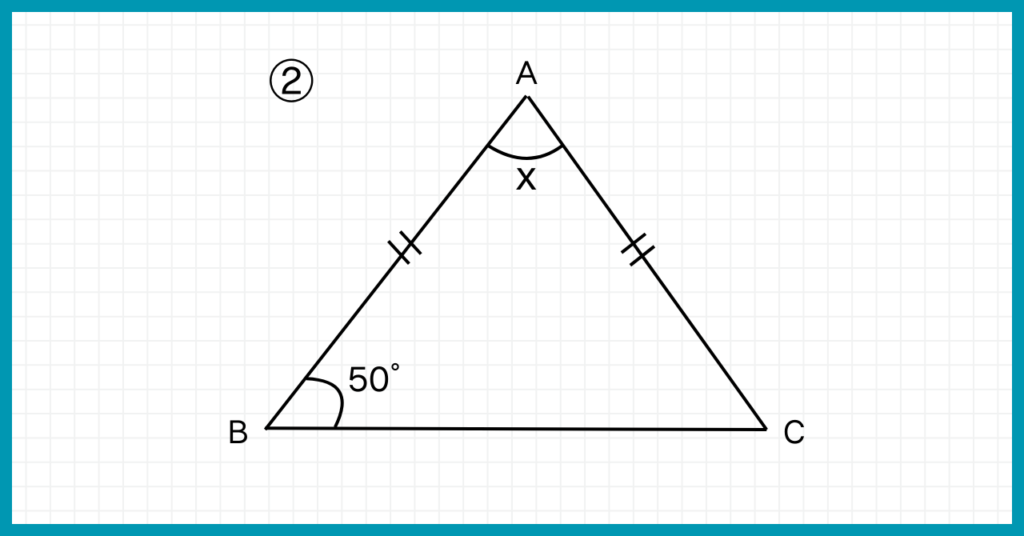
角度が一個しか書いてないじゃないか！

　慌てないで、底角の大きさが等しいことを思い出しましょう。

　底角が50°とわかっているので、もう片方の底角も50°ですね。

まとめ

　二等辺三角形の単元では、証明問題のような難しい問題を扱います。

　しかしこの記事で扱った二等辺三角形の角度を求める問いは、解き方を覚えてしまえば簡単に攻略できます。

　テストで得点源にするために、問題演習を重ねて確実にマスターしましょう。