【中2数学】二等辺三角形の証明問題『よく出る2つのポイント』を解説

　二等辺三角形の証明をしなさいと言われて、どのように証明したらよいかわからない人がいるのではないでしょうか。

　三角形の合同証明のように合同条件を暗記させられるわけではないので、戸惑ってしまいますよね。

　この記事では、二等辺三角形であることを証明する方法の、よく出る2パターンを解説します。

　それぞれのパターンを用いた例題もあるので、二等辺三角形を証明する方法の基礎が身につきますよ。

二等辺三角形であることを証明するポイント2つ

　二等辺三角形であることを証明するためには、以下の根拠を示すパターンがあります。

　特に底角の大きさが等しいことを示すパターンが頻出です。

【例題】二等辺三角形であることを証明する問題2パターン

　ここからは二等辺三角形であることを証明する例題をやっていきましょう。

【頻出】①底角の大きさが等しい

　まずは頻出の、底角の大きさが等しいことを示すパターンをやっていきます。

例題①

△ABCは二等辺三角形である。

DB=ECのとき、△FBCが二等辺三角形であることを証明せよ。

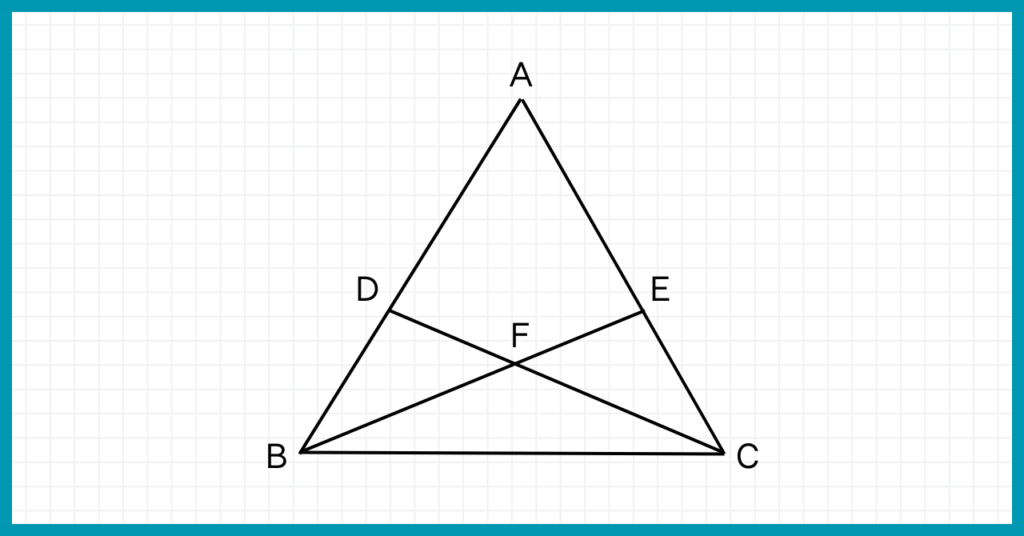
　△FBCが二等辺三角形であることを言うため、底角の大きさが等しいことを示しましょう。

　△FBCの底角は∠FBCと∠FCBですね。

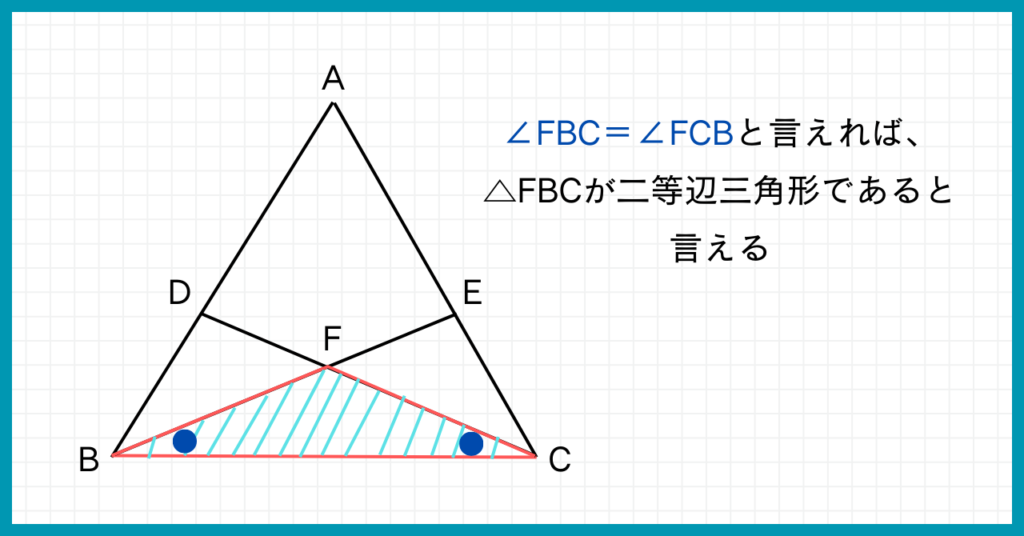
　さて、△FBCの底角と共通の角をもつ三角形があります。

∠FBCは△EBCが、

∠FCBは△DBCがもっているね

　そこで、△EBCと△DBCの合同を証明しましょう。

　合同な図形の対応する角は等しいので∠EBC＝∠DCB、つまり△FBCの底角が等しいので△FBCは二等辺三角形であると言えます。

解答

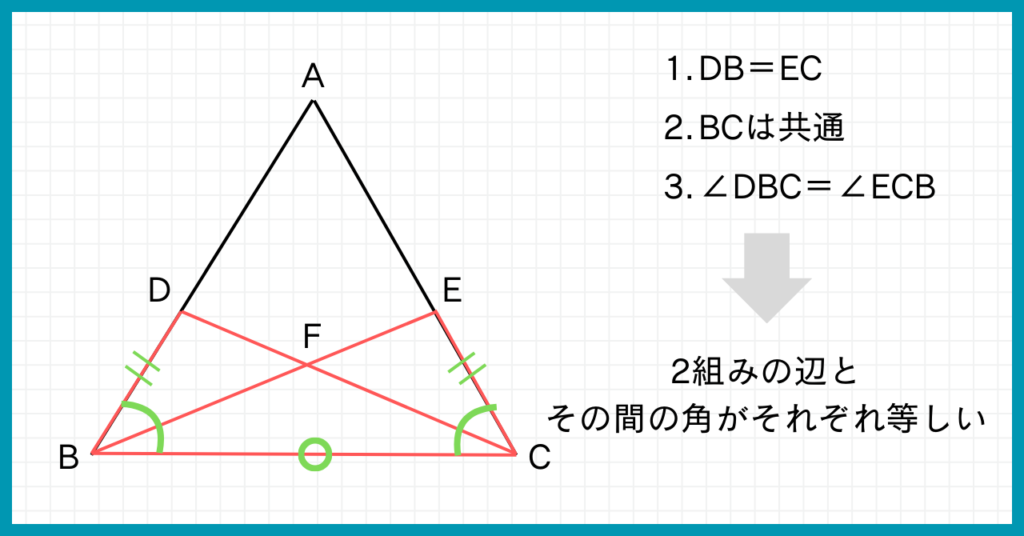
△DBCと△ECBにおいて

仮定よりDB＝EC…①

BCは共通…②

また、△ABCは二等辺三角形なので、∠DBC＝∠ECB…③

①②③より、2組みの辺とその間の角がそれぞれ等しいので△DBC≡△ECBである。

合同な三角形の対応する角は等しいので、∠FBC＝∠FCB

よって△FBCの底角が等しいので、△FBCは二等辺三角形である。

②2辺の長さが等しい

　次は2辺の長さが等しいことを示すパターンです。

例題②

四角形ABCDは長方形である。また、点MはADの中点である。

このとき、△MBCが二等辺三角形であることを証明せよ。

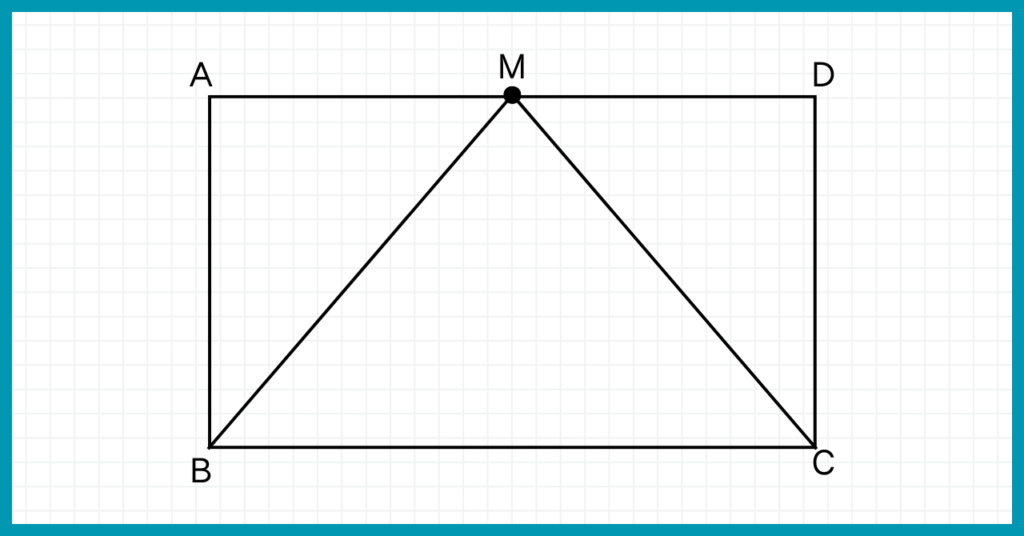
　三角形の合同を証明する方法で、MB＝MCを示しましょう。

　MB＝MCを言うために、それらの辺を含む三角形である△AMBと△DMCの合同を証明すればよさそうですよね。

解答

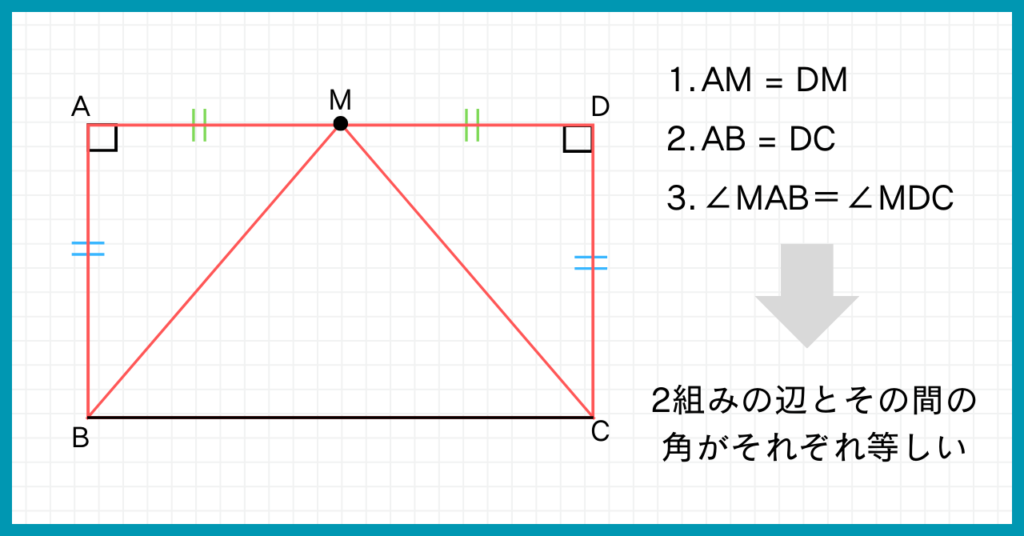
△AMBと△DMCにおいて

点Mは辺ADの中点なので、AM = DM…①

四角形ABCDは長方形なのでAB = DC…②

さらに∠MAB＝∠MDC＝90°…③

①②③より2組の辺とその間の角がそれぞれ等しいので、△AMB≡△DMC

合同な三角形の対応する辺は等しいので、MB=MC

よって△MBCの2辺が等しいので、△MBCは二等辺三角形である。

まとめ

　二等辺三角形を証明する問題を難しそうに感じてしまうかもしれません。

　しかし三角形の合同証明の方法がわかり、また二等辺三角形の性質を知っていれば難しいことはないのです。

　三角形の合同証明や二等辺三角形の性質を忘れてしまった人はそこから復習しましょう。