【方程式なし】ラクしておうぎ形の中心角を求める方法

　おうぎ形の弧の長さや面積を求める公式は教科書に載っているし、授業でもしっかり習うことでしょう。

　それに対して、おうぎ形の中心角を求める公式はありません。おうぎ形の面積や弧の長さを求める公式を用いて方程式を作り、おうぎ形の中心角を求めます。

　公式がないのに、おうぎ形の中心角を求める問いは頻繁に出てくる。しかも方程式を作って求めなきゃいけないのが面倒くさい……。

　あなたが戸惑うのも無理はありません。

　この記事では、おうぎ形の中心角を方程式を使わずに求める方法を解説します。

　この記事を読めば、おうぎ形の面積や弧の長さを求める公式を用いて方程式を作る方法よりも簡単に、おうぎ形の中心角を求められるようになりますよ！

【基本】おうぎ形の中心角を方程式で求めると面倒

　まずは王道の方法『弧の長さや面積を求める公式を用いて方程式を作る方法』で考えてみましょう。

　①は弧の長さの公式、②は面積を求める公式に代入し、中心角aを求めます。

　①について。

　弧の長さを求める公式$l=2πr×\frac{a}{360}$より、弧の長さが12$π$cm、半径が18cmなので

　$12π=2π×18×\frac{a}{360}$

　$a=120$

　よって中心角は120°

　②について。

　面積を求める公式$S=πr^2×\frac{a}{360}$より、面積が16$π$cm、半径8cmなので

　$16π=8^2π×\frac{a}{360}$

　$a=90$

　よって中心角は90°

　おうぎ形の中心角を求めるには、方程式を用いるのが基本です。

　でも、方程式を解くのってちょっと面倒じゃないですか？

　方程式なして中心角を求める方法が、実はあるんです！

おうぎ形の中心角を方程式なしで求める方法

　面倒な方程式を解かなくても、おうぎ形の中心角は求められます。

　実は、ちょっとしたかけ算をするだけでおうぎ形の中心角を求められます！

　ここからはその方法を解説します。

【前提知識】おうぎ形は円の一部

　実は方程式なんか解かなくても、ちょっとしたかけ算をするだけでおうぎ形の中心角を求められます。

　その方法を理解するため、まずはおうぎ形は円の一部であることをおさらいしましょう。

　円をピザ1枚とみると、おうぎ形はピザ1切れです。

　このことから理解してほしいのは、おうぎ形の弧の長さは円周の一部だし、おうぎ形の面積は円の面積の一部であることです。

【公式】面積や弧の長さの比から中心角を求める方法

　まずは中心角を求める公式を見てみましょう。

　おうぎ形の中心角を求める問いで、弧の長さが与えられている場合は①、面積が与えられている場合は②の式を使います。

①の円周の長さとか、②の円の面積って、

なんの円のことなの？

　式に出てくる円周や円の面積とは、中心角を求めたいおうぎ形を一部としている円の円周や面積のことです。

　おうぎ形の中心角は、弧の長さや面積が元の円よりどれくらい小さいのかが分かれば求められるのです。

　例えば半径18cm、弧の長さが12$π$cmのおうぎ形を円の一部と見ましょう。

　では、その円の円周の長さはいくつでしょうか？

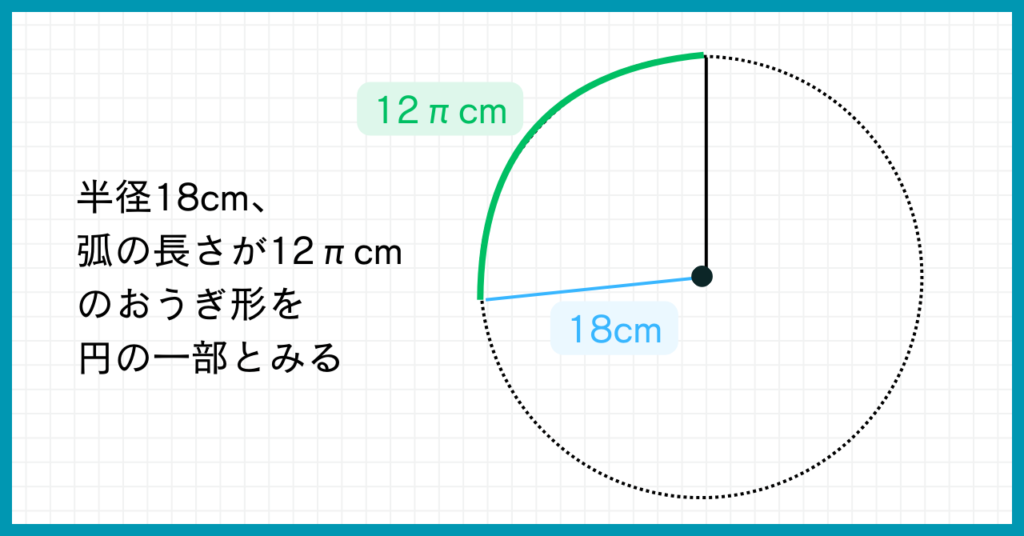
　おうぎ形の半径と、元の円の半径は変わらないので、円の半径も18cm

　よって円周は$2×18×π=36π(cm)$

　おうぎ形の弧の長さは12$π$cmで、円周の長さは36$π$cm

　$\frac{12}{36}$より、おうぎ形の弧の長さは円周の$\color{red}{\frac{1}{3}}$です。

　つまりこのおうぎ形の中心角は、円全体(360°)の$\color{red}{\frac{1}{3}}$の大きさであるというわけです。

　(後で解答をまとめますね)

【例題】弧の長さと円周の比から中心角を求めてみよう

　この求め方を使って、以下の例題を解いてみましょう。

　①について。

　弧の長さが分かっているので、$360×\frac{(おうぎ形の弧の長さ)}{(円周の長さ)}$を用いて中心角を求めましょう。

　このおうぎ形を円の一部とみると、元の円も半径18cmなので円周の長さは$2×18×π=36π(cm)$

　よって$360×\frac{(おうぎ形の弧の長さ)}{(円周の長さ)}$より

　$360×\frac{12π}{36π}$

　$=360×{\color{red}{\frac{1}{3}}$

　$=120$

　よって中心角は120°です。

おうぎ形の弧の長さは円周の長さの$\frac{1}{3}$だから、

中心角も円全体(360°)の$\frac{1}{3}$なんだね。

　②について。

　面積が分かっているので、$360×\frac{(おうぎ形の面積)}{(円の面積)}$を用います。

　このおうぎ形を円の一部とみると、元の円も半径8cmなので円の面積はは$8×8×π=64π(cm^2)$

　よって$360×\frac{(おうぎ形の面積)}{(円の面積)}$より

　$360×\frac{16π}{64π}$

　$=360×{\color{red}{\frac{1}{4}}$

　$=90$

　よって中心角は90°です。

おうぎ形の面積は円の面積の$\frac{1}{4}$だから、

中心角も円全体(360°)の$\frac{1}{4}$なんだね。

まとめ

　方程式を使わずにおうぎ形の中心角を求める方法をまとめます。

　おうぎ形の中心角を求める問いは、方程式を解くのでミスをしやすいです。

　この記事で紹介した方法なら、方程式を解くよりも計算が簡単なので、ぜひこの方法をマスターしてください。