【高校入試】作図の問題を解くコツと重要な基礎知識を解説

　過去問や模試の作図の問題って難しいですよね。

　学校で習ったときはサラッと流されてしまい、それ以降は作図が授業で出てこないため、中3になってから苦労している人が多いことでしょう。

　ところで、『角の二等分線』は何を表す線ですか？

え、角を二等分するための線じゃないの？

　それしか知識が出てこないなら、不十分です。

　入試問題の作図を解けなくても無理はありません。

　この記事では、模試や入試本番で作図の問題を解くコツを解説します。

　また、模試や入試本番で作図の問題を解くために重要な基礎知識も解説しています。

【高校入試】作図の問題を解くコツ

　まずは作図の問題を解くコツを解説します。

• 『垂線』『角の二等分線』『垂直二等分線』を使いこなすこと
• 『角の二等分線』『垂直二等分線』の重要な性質を知ること

　以下で詳しく解説します。

『垂線』『角の二等分線』『垂直二等分線』を使いこなすこと

　作図の問題をどうやって解いたらいいかわからない人に朗報です。

　作図の問題は、『垂線』『角の二等分線』『垂直二等分線』の3つが描ければ解けます！

　この3つの作図を組み合わせて問題に答えていけばよいのです。

　『垂線』『角の二等分線』『垂直二等分線』の書き方がわからない人は、まずはそこから勉強しましょう。

『角の二等分線』『垂直二等分線』の重要な性質を知ること

　角の二等分線や垂直二等分線は、どんな線でしょうか？

角の二等分線は角度を二等分する線だし、

垂直二等分線は垂直で二等分な線じゃないの？

　角の二等分線や垂直二等分線についてそれぐらいしか答えられないなら、入試問題の作図は解けません。

　角の二等分線と垂直二等分線について、以下の性質を覚えてください。

　角の二等分線と垂直二等分線の性質は忘れがちですが、入試問題を解くために必須の知識です。

　この後で詳しく解説するので、そのままスクロールしてくださいね。

【重要知識】『角の二等分線』『垂直二等分線』の性質を図解

　ここからは『角の二等分線』『垂直二等分線』の重要な性質を図解します。

• 角の二等分線は『2つの直線から』から等しい距離を表す直線
• 垂直二等分線は『2つの点』から等しい距離を表す直線

　『角の二等分線』『垂直二等分線』の性質は、高校入試の作図を攻略するための重要な基礎知識です。

　角の二等分線は角を二等分するだけ、垂直二等分線は垂直かつ二等分するだけ、と思っている人は読んでくださいね。

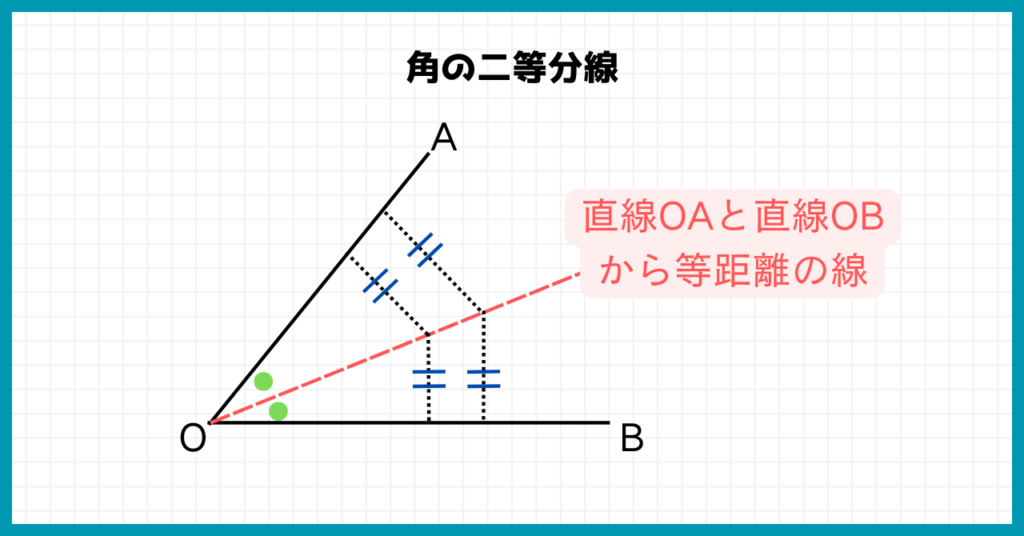
角の二等分線は『2つの直線』から等しい距離を表す直線

　角の二等分線で重要なのは、なんと角ではありません。

　角を作っている2つの直線が重要です。

『角の二等分線』の性質

角を作っている2つの直線からの距離が等しい直線を表す。

　角の二等分線の活用例を見ていきましょう。

活用例

コンパスを用いて、直線AB、直線BC、直線CDとの距離が等しい点Pを作図せよ。

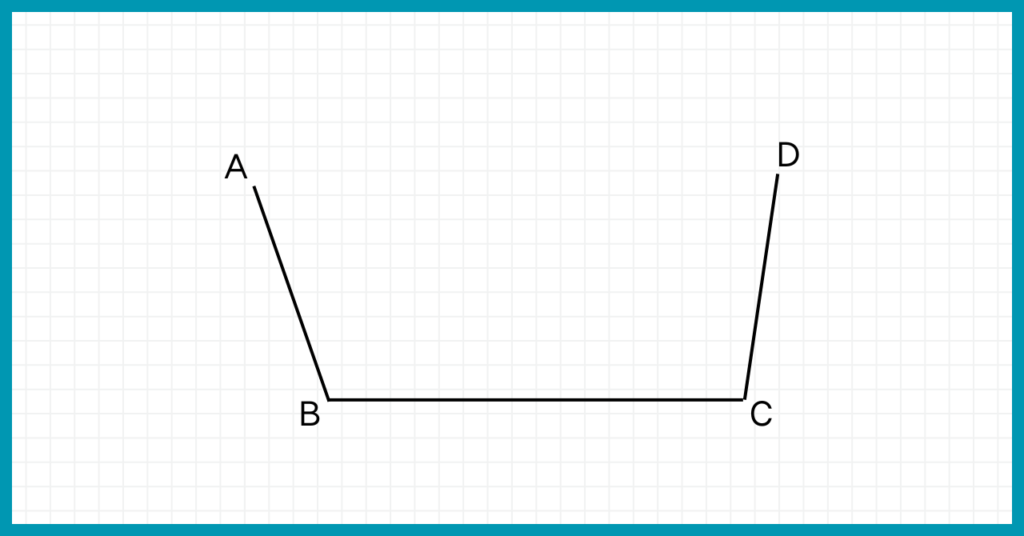
　直線との距離が等しい点を作図するということは、角の二等分線を使います。

でも、3つの直線から等しい距離の点を描かなきゃいけないんでしょ？

角の二等分線じゃ、2つの直線と等距離の直線しかわからないよ？

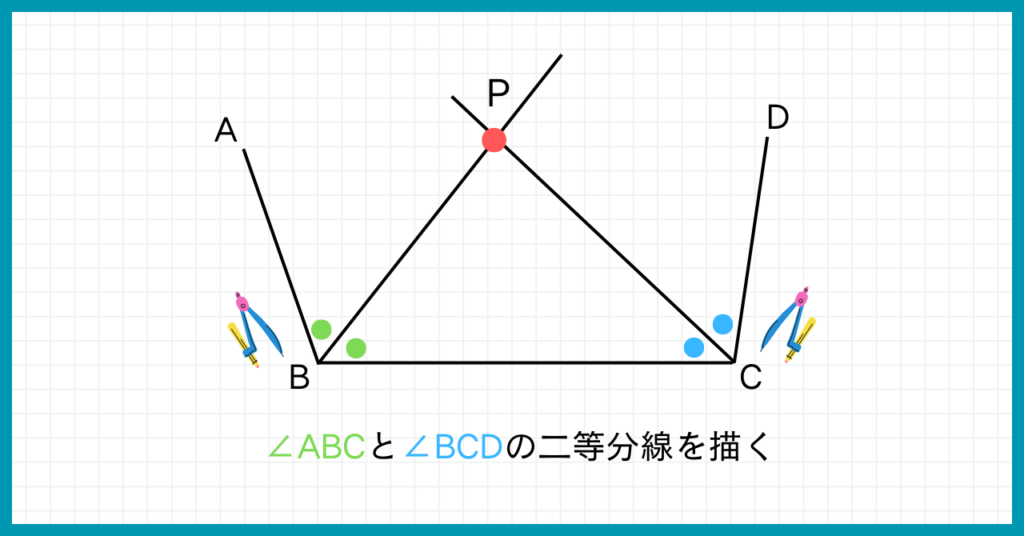
　直線AB、直線BC、直線CDの3つの直線と等しい距離の点を探すためには、『直線ABと直線BCに等しい距離の直線』と『直線BCと直線CDに等しい距離の直線』を引きましょう。

　そうしてできた2つの直線の交点こそが、直線AB、直線BC、直線CDの3つの直線と等しい距離の点なのです。

直線ABと直線BCに等しい距離の直線は、∠ABCの二等分線、

直線BCと直線CDに等しい距離の直線は、∠BCDの二等分線だね！

解答

垂直二等分線は『2つの点』から等しい距離を表す直線

　垂直二等分線で重要なのは直線ではなく、2つの点です。

『垂直二等分線』の性質

2つの点から等しい距離を表す直線を表す。

　上図でいうと、この垂直二等分線は点Aと点Bから等しい距離を表しています。

△PABは二等辺三角形になるんだね！

　垂直二等分線の活用例を見ていきましょう。

活用例

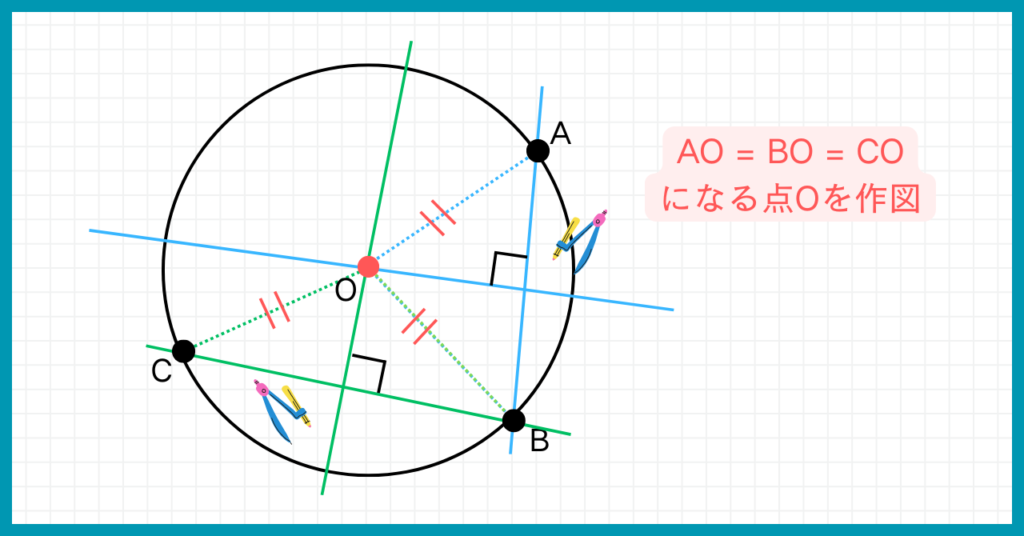
コンパスを用いて点A、点B、点Cを通る円を描きなさい。

　この問いではまず、点A、点B、点Cを通る円の中心はどこなのかを考えましょう。

　円周上の点であれば全て、円の中心までの距離は等しいことを利用して、円の中心を探します。

　つまり、点A、点B、点Cの3点から等しい距離にある一点が、3点を通る円の中心なのです！

3つの点から等しい距離にある点って、どうやって求めるの？

　垂直二等分線とは、2つの点から等しい距離を表す直線でしたよね。

　まず点Aと点Bを結び、垂直二等分線を描きます。

　さらに、点Bと点Cを結び垂直二等分線を描きましょう。

　この2つの垂直二等分線の交点が、点A、点B、点Cの3点から等しい距離にある一点、つまり円の中心Oです。

解答

まとめ

　作図の問題を苦手としている人は多いことでしょう。

　しかし、作図の問題は『垂線』『角の二等分線』『垂直二等分線』の3つが描ければ解けるのです。

　問題はその3つをどう使うか、ということですが、角の二等分線と垂直二等分線の役割をしっかり理解していれば決して難しくはありません。

　あとは過去問や問題集を用いて、作図問題の経験値を増やしていきましょう。