【中3数学・相似】面積比と体積比を用いた『円錐内の水』の問いを解説
中3数学『相似』のラスボスといえば、面積比・体積比を用いて解く『円錐内の水』の問いです。
私が塾講師として生徒を見ていると、ほとんどの人が『円錐内の水』の問いでつまづいています。
しかし、相似比と面積比・体積比の関係がわかれば簡単に解けるようになりますよ!
この記事では、まずは前提知識として相似比と面積比・体積比の関係を確認します。
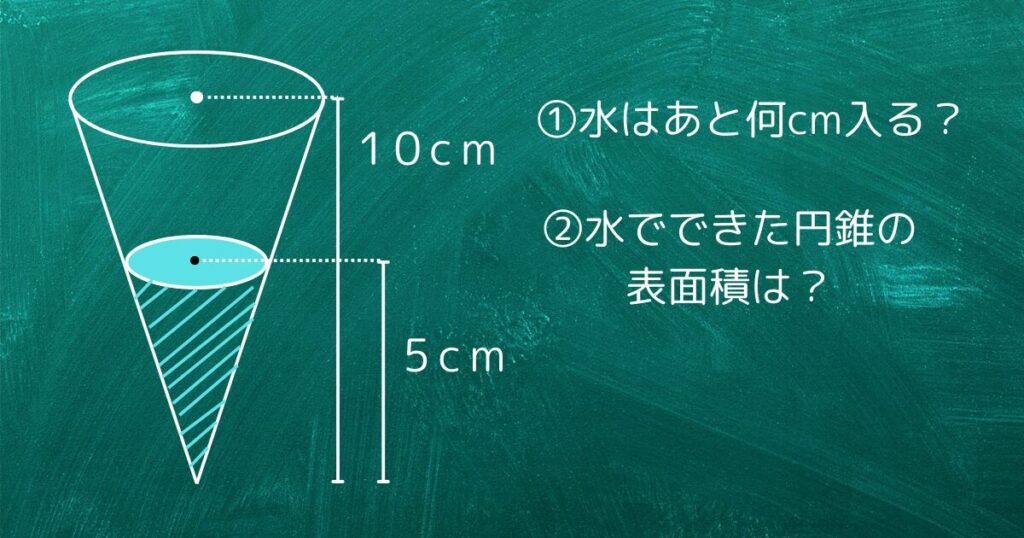
その後で、円錐内の水の問い、①水はあとどれくらい入るか、②水で出来た円錐の表面積はいくらかを解説します。
【前提知識】相似比と面積比・体積比との関係
まずは相似比と面積比・体積比の公式を確認します。
その後で相似比から面積比・体積比を用いる例題を行い、公式をきちんと使えるかを確認します。
これくらいは余裕だよ! という人は読み飛ばしOKです。
①相似比と面積比・体積比の公式
まずは相似比と面積比・体積比の公式を確認しましょう。
②面積比・体積比を用いる基礎例題
次に、相似比を用いて面積比・体積比を求める基礎的な例題を行います。
例題
△ABCと△DEFの相似比が2:3のとき、以下の問いに答えましょう。
- 面積比と体積比は?
- △ABCの面積が10$cm^2$のとき、△DEFの面積は?
①について。
面積比は$2^2:3^2={\color{red}{4:9}}$
体積比は$2^3:3^3={\color{red}{8:27}}$
②について。
①より、△ABCと△DEFの面積比は$4:9$なので、△DEFの面積は
$4:9=10:x$
$x=22.5$
よって$\color{red}{22.5cm^2}$
面積比と体積比を用いた『円錐内の水』の問いを解説
次からはいよいよ、面積比と体積比を用いた『円錐内の水』の問いを解説します。
問題は以下です。
問題
円錐の入れ物の中に水を入れたとき、次の問いに答えましょう。
- 円錐の入れ物に水を$80cm^3$入れたとき、水はあと何$cm^3$入る?
- 円錐の入れ物の底面の半径が7cmのとき、水でできた円錐の表面積は?
解説はこの後です。
①水はあと何$cm^3$入る?
水の入っている部分を円錐と見ると、水でできた円錐と、円錐の入れ物の相似比は、
$5:10=1:2$
よって体積比は$1^3:2^3=1:8$
さて、水の体積がわかっているので、体積比から入れ物の体積を求められます。
そして(入れ物の体積)-(水の体積)をすれば、あと何$cm^3$の水が入るかがわかります。
$1:8=80:x$
$x=640$
よって入れ物の体積は$640cm^3$なので、
640-80=560
よって答えは$\color{red}{560cm^3}$
②水でできた円錐の表面積は?
この問いを解く鍵は、円錐の入れ物の表面積です。
それさえ計算できれば、あとは面積比から水で出来た円錐の表面積を求められます。
さて、円錐の表面積を求める方法を覚えているでしょうか?
円錐の表面積を求めるポイントは、側面のおうぎ形の、中心角を求めることです。
忘れてしまった人はこの記事を参考にしてくださいね。
円錐の入れ物の展開図を見てみましょう。
このように、円錐を展開すると、『円』とおうぎ形に分れます。
円錐の表面積を求めるためには、それぞれの面積の和を求めればよいのです。

おうぎ形の中心角がないよ?
おうぎ形の中心角を求める方法は、
- 底面の円の円周=おうぎ形の弧の長さ
- おうぎ形の弧の長さを求める公式から中心角を求める
以上の2つがポイントです。
円の半径が7cmなので、$円周の長さ=2πr=2×π×7=14π(cm)$
よっておうぎ形の弧の長さも$14π(cm)$
次におうぎ形の弧の長さを求める公式に代入して、おうぎ形の中心角を求めましょう。
おうぎ形の弧の長さ=$14π(cm)$、おうぎ形の半径=$10cm$で、中心角をa°とすると
$14π=2×π×10×\frac{a}{360}$
$a=150°$
よって、円錐の入れ物の表面積は、
$(底面の円の面積)+(側面のおうぎ形の面積)$
$=7×7×π+10×10×π×\frac{150}{360}$
$=49π+\frac{125}{3}$
$=\frac{250}{3}cm^2$
ここからが本題です。
水でできた円錐と円錐の入れ物の相似比は$5:10=1:2$
よって面積比は$1:4$です。
さっき円錐の入れ物の体積を求めたので、この面積比から、水で出来た円錐の表面積を求めます。
$1:4=x:\frac{250}{3}$
$x=\frac{125}{6}$
よって、水で出来た円錐の表面積は$\color{red}{x=\frac{125}{6}cm^3}$
まとめ『相似比と面積比・体積比の関係と円錐の問い』
相似比と面積比・体積比の関係と円錐の問いについてまとめます。
円錐の問題では、円錐の表面積を求める方法のような、中1で習った内容がでてきます。
難しく見えるかも知れませんが、既に習った内容を一つ一つ振り返れば、必ずできるようになりますよ。

コメントを残す