【中3数学】多項式の文章題「図形への利用」は簡単!解き方を3ステップで解説

公立中学の3年生にとって、数学で初めにぶつかる壁といえば「多項式の文章題」ですよね。
展開・因数分解の計算自体は楽勝でも、その後の文章題で躓いてしまうことでしょう。特に図形の問題は、文章と図形が一緒にかいてあるだけで嫌になってしまいますよね。
しかし多項式の文章題はたったの3ステップ『①聞かれていることは何かを確認する』『②聞かれていることに答えるのに必要な式を立てる』『③式の計算をする』で解くことができます。
文章題を前に途方に暮れてしまう人でも、この記事を読めば多項式の文章題を解く3ステップが分かり、問題を解けるようになりますよ!
多項式の文章題『図形への利用』の解き方3ステップ
多項式の文章題『図形への利用』の解き方3ステップは以下です。
- 聞かれていることは何かを確認する
- 聞かれていることに答えるための式を作る
- 式の計算をする
次の例題を用いながら解説します。
例題
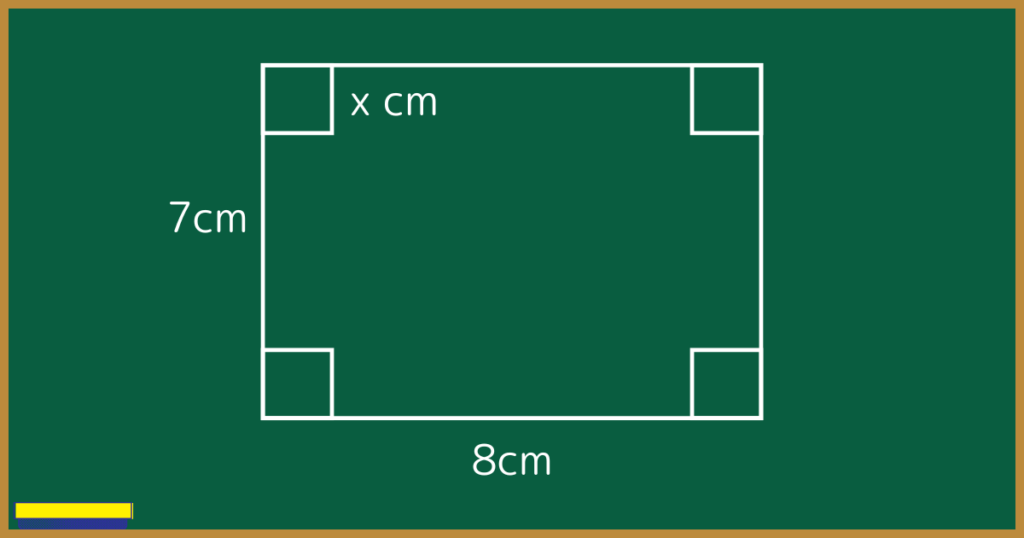
縦$7cm$、横$8cm$の厚紙の四方から、一辺$xcm$の正方形を切り取った。
このとき、この厚紙を用いてできる直方体の容積を求めよ。
ステップ1:聞かれていることは何かを確認する
文章題を解く上で大切なのは、何を聞かれているのかを把握することです。
この例題の場合、聞かれているのは『直方体の容積』です。
ステップ2:聞かれていることに答えるための式を作る
ステップ2では聞かれていることに答えるための式を作ります。
ステップ1で、この例題では直方体の容積を聞かれているとわかりました。
では、直方体の容積を求めるためには、どんな式を作ればいいでしょうか?

直方体の容積の公式は、
底面積×高さ
だね。
容積を求めるためには、底面積と高さが何かを考える必要があります。
聞かれていることに答えるために必要な式を立てるためには、問題文の状況を読み取ります。
この問題の場合、状況とは『縦$7cm$、横$8cm$の厚紙の四方から、一辺$xcm$の正方形を切り取った』です。
この状況を読み取り、直方体の容積を求める式に必要な『底面積』と『高さ』を文字で表します。
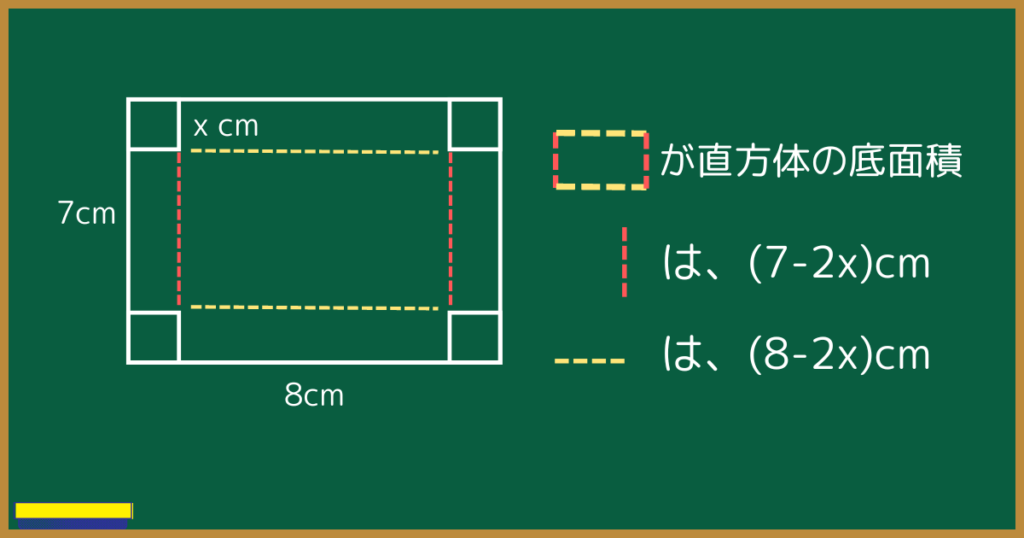
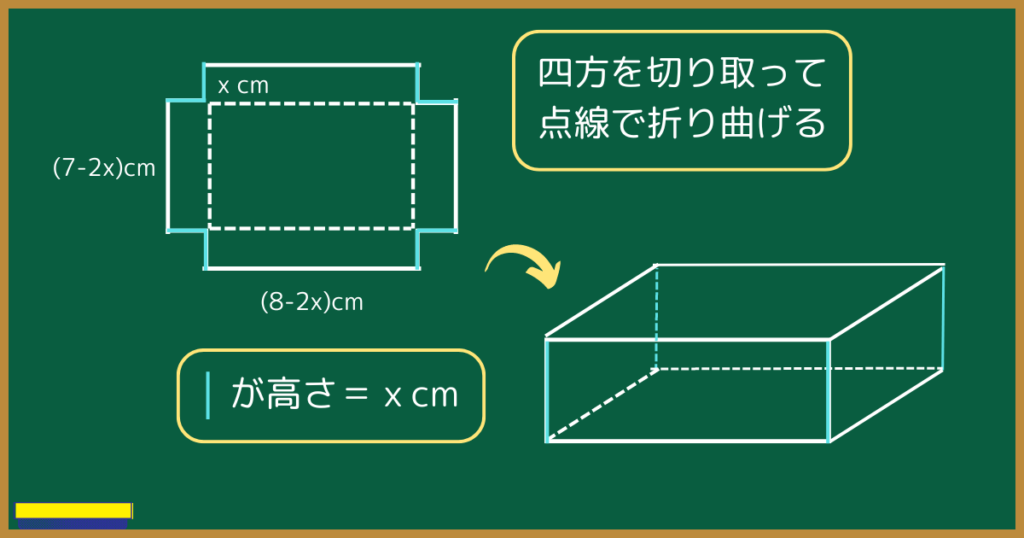
実際に問題を解くときは、縦や横、高さを書き込みながら考えるとミスが減ります。
ステップ3:式の計算をする
式を作ったら、あとは計算をするだけです。
多項式の文章題では展開をすることがあるので、展開の方法を忘れてしまった人は復習しましょう。
直方体の容積は、
$(7-2x)×(8-2x)×x$
$=x(56-14x-16x+4x^2)$
$=4x^3-30x^2+56x$
よって直方体の容積は$4x^3-30x^2+56x({cm}^3)$
【問題演習】多項式の文章題「図形への利用」を解いてみよう
上に書いてある『多項式の文章題の解き方3ステップ』に則り、問題を解いてみましょう。
問題
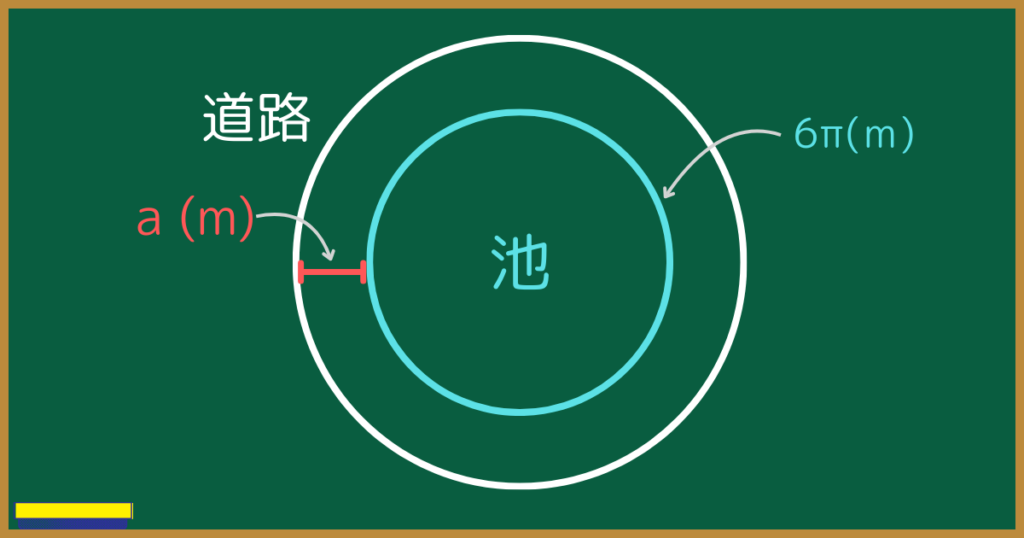
周の長さが$6π(m)$の池の周りに、道幅$a(m)$の道路がある。
このとき、道路の面積を求めよ。
まずはステップ1『聞かれていることを確認』しましょう。

聞かれているのは『道路の面積』だね
次にステップ2『聞かれていることに答えるための式』を作ります。
上の例題のように、公式ひとつでは道路の面積を求められませんよね。

道路の外側の線を円とみて、そこから池の面積を引けば良いんじゃないかな?

上の図のように『$(道幅+池の面積)-(池の面積)$』をすれば、道路の面積を求められます。
まずは(道幅+池の面積)を文字で表してみましょう。

(道幅+池の面積)は道幅の外側の線を円とみれば求められるね。
この円の半径は、(道幅+池の半径)だ。

道幅の長さは$a(m)$だ。
あれ? 池の半径がわからないぞ?
では、池の半径を求めてみましょう。
この問題の状況を見ると、『周の長さが$6π(m)$の池の周りに、道幅$a(m)$の道路がある。』と書いてあります。
池の半径を求めるのに使うのは、池の周の長さです。

周の長さの公式は『$2πr$』だね。
$π$は円周率で$r$が半径だ!
つまり、池の周の長さ$2πr=6π$なので、方程式を解けば半径rが出ます。

$2πr=6π$より、
$r=3(m)$だ!
こうして、池の半径が$3m$だとわかりました。
つまり道幅の外側の線を円と見るとその半径は、(道幅+池の半径)なので$a+3(m)$です。
また、池の面積は、池の半径が$3m$なので、$(道幅+池の面積)-(池の面積)$の式は以下のようになります。
$(道幅+池の面積)-(池の面積)$
$=π(a+3)^2-3^2π$

最後に、ステップ3『式の計算』をしましょう。
以下で解答をまとめます。
解答

池の周の長さは$6π(m)$なので、$2πr=6π$より、$r=3$
よって池の半径は$3m$
道幅の面積は$(道幅+池の面積)-(池の面積)$で求められるので、式は以下のようになる。
$π(a+3)^2-3^2π$
$=π(a^2+6a+9)-9π$
$=πa^2+6πa$
$=πa(a+6)$
よって、道路の面積は$πa(a+6)m^2$
まとめ~問題文を正しく読めれば簡単!
多項式の文章題『図形への利用』を解く3ステップは以下でした。
- 聞かれていることは何かを確認する
- 聞かれていることに答えるための式を作る
- 式の計算をする
多項式の文章題に限らず、全ての文章題でこの3ステップは使えます。
文章題に出会ったらまずは冷静に、聞かれていることは何かを把握しましょう。
それさえ理解できれば、あとはどうにかなるものですよ。

コメントを残す