中学3年生になって、受験を意識し始めた人も多いのではないでしょうか。
内申点にも影響するし、次のテストで高得点を取りたい！
中3の初めは展開・因数分解といった計算問題を多く習うので、中3最初のテストでは比較的点数が取りやすくなります。
こういう時こそ、しっかり勉強してテストで高得点を狙いましょう！
展開は乗法公式を覚えるだけだから余裕！
そう考えている中学生諸君、ちょっと待った！
確かに、展開は公式を覚えるだけで解けてしまうけど、本当に丸暗記だけをしているとミスをしてしまうかもしれないんだ。
ここでは、展開公式の意味と色々な問題に対応できる覚え方を紹介します。
乗法公式の話をする前に、まずは分配法則を用いた展開について見ていこう。
$$(a+b)(c+d)$$
$$=ac+ad+bc+bd$$
例 $$(ｘ+3)(ｙ-2)＝ｘｙ-2ｘ+3ｙ-6$$
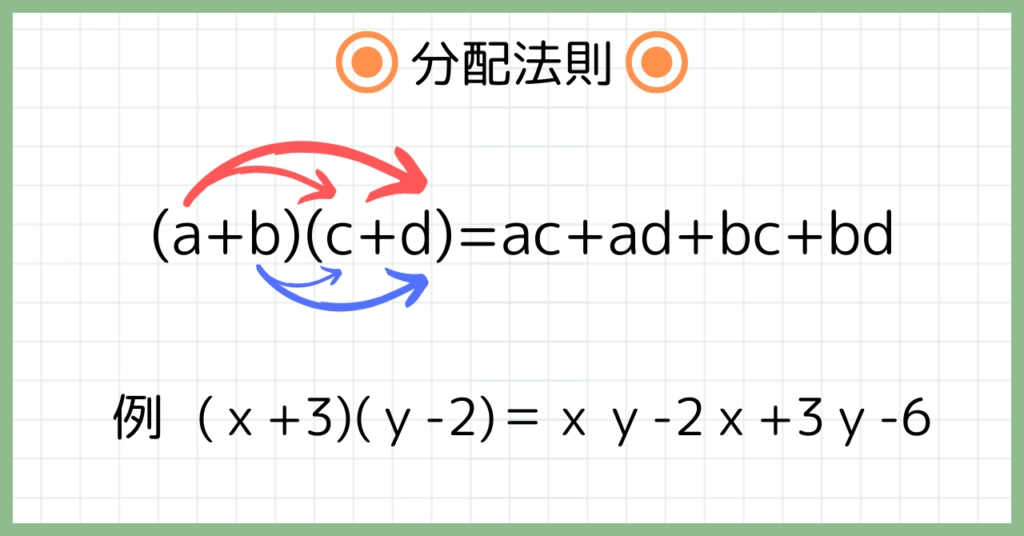
これからお話しする乗法公式は、全てこの分配法則が基本になっています。
じゃあ、分配法則だけ覚えていればいいの？
最悪それでも問題は解けるけど、公式を使った方が早いのでテストまでには必ずマスターしておこう。
乗法公式
(x+a)(x+b)=x2+(a+b)ｘ+ab
みなさんが一番初めに習う公式です。これが一番覚えにくいので、これを見て、色のイメージで覚えてみましょう。
(x+a)(x+b)
=x2+(a+b)ｘ+ab
つまり、
左２+(右+右)×左+右×右
というように覚えましょう！
ポイントは、数字だけでなく符号も含めて計算すること。そうすることで符号ミスを減らすことができます。符号にも色を付けているのはそういう理由からです。
-
(x+2)(x+3)…① (x+5)(x-7)…➁を展開せよ
-
①(ｘ+２)(ｘ+3)
=ｘ2+(2+3)x+2×3
=ｘ2+5x+6②(x+5)(x-7)
=x2+(5-7)x+5×(-7)
=x2-2x-35
公式暗記すればいいんじゃないの？
じゃあ、(2x+3)(2x-2)を解いてみよう。
あれ？ｘに係数がついてる…？
なぜわざわざ右や左みたいに覚えてもらったかというと、文字に係数がついたときでもミスをしないようにするためなんだ。
-
(2x+3)(2x-2)を展開せよ
-
(2x+3)(2x-2)
=(2x)2+(3-2)×2x+3×(-2)
=4x2+2x-6
教科書に書いてある公式を丸暗記していると、特に真ん中の項に2xの2をかけ忘れてしまうミスをしてしまう。
ぜひ、右、左…と唱えながら問題演習をしてみてください！
(x+a)2=x2+2ax+a2
(x-a)2の公式もあるよね！
教科書では(x+a)2と(x-a)2の両方の公式が書いてあると思うけど、片方だけ覚えていればいい。
(x+a)2
=x2+2ax+a2
=左2+2×右×左+右2
これは(x+a)2の公式だけど、この右と左にあてはめて(x-a)2の問題を解いてみよう。
-
(x-3)2を展開せよ
-
(x-3)2
=x2+2×(-3)×x+(-3)2
=x2-6x+9
こんなふうに、わざわざ公式を覚えなくても(x-a)2の展開ができます！
(x+a)(x-a)=x2-a2
これは一番特徴的な公式ですね！
(x+a)(x–a)
=x2–a2
=左2–右2
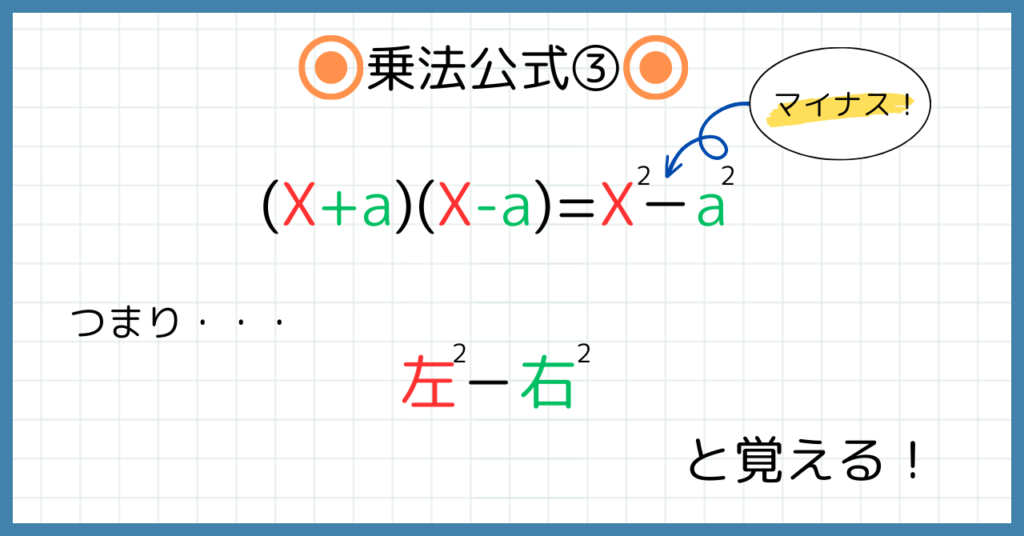
ポイントは、左右がそれぞれ同じもので、符号だけが異なるときに使えるということです。
これは楽勝だ！
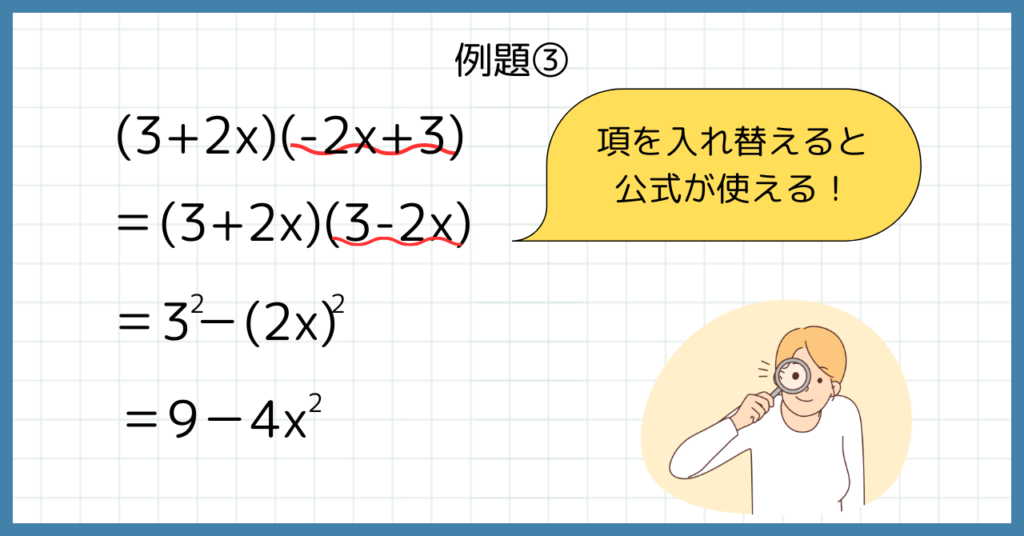
じゃあ、(3+2x)(-2x+3)はどうかな？
これじゃ公式が使えないから分配法則するしかないじゃん！
本当にそうかな？
右側のカッコの中にある項を入れ替えると…
(3+2x)(3-2x)だ！
こうして向きをそろえれば、公式を使って展開できます！
解答は以下です。
(3+2x)(-2x+3)
=(3+2x)(3–2x)
=32-(2x)2
=9-4x2
まとめ
展開は3年生の内容の中でもとくに得点を稼ぎやすい単元ですが、公式が多く混乱してしまい失点することがあります。
この記事で挙げたように、右、左…と頭の中で唱えながら問題演習を積めば、必ず展開をマスターできます！
公式は覚えるのではなく使いこなせるようにしていきましょう！