【都立高校入試】数学大問1『円周角』対策方法とポイント5選を解説

　都立高校入試の数学では、大問1を死守することが重要ですよね。

　しかし円周角の問題が思ったよりも難しくて、困っているのではないでしょうか？

　この記事では都立高校入試を受けるあなたに向けて、数学大問1『円周角』の対策法と、円周角の問題を解くポイントを5つ紹介します。

　この記事を読めば円周角の問題を解けるようになり、模試や入試本番でも実力を発揮できるようになりますよ！

【対策法】都立高校入試の円周角を解けるようになるには？

　都立高校入試の過去問を見たり、模試を受けたあなたならわかるかもしれません。

　都立高校入試の円周角の問題は、パッと見ただけですぐに解けるほど簡単ではありませんよね。

　都立高校入試の円周角の問題を解けるようになるためには、教科書の節末問題や章末問題レベルの問いを演習しましょう。

　学校の問題集で言うと、標準～応用問題レベルです。

円周角の応用問題なんて、どうやって解いたらいいかわからないよ～

　そんなあなたのために、この先では都立高校入試で円周角の問題を解くポイントを紹介するので、目を通してくださいね。

　そもそも基礎的な問題から怪しい！　という人は以下の記事から読んでくださいね。

都立高校入試大問1『円周角』を解くポイント5選

　ここからは都立高校入試大問1『円周角』を解くポイントを5つ紹介します。

　以下で詳しく解説します。

①円周角の大きさは中心角の大きさの半分

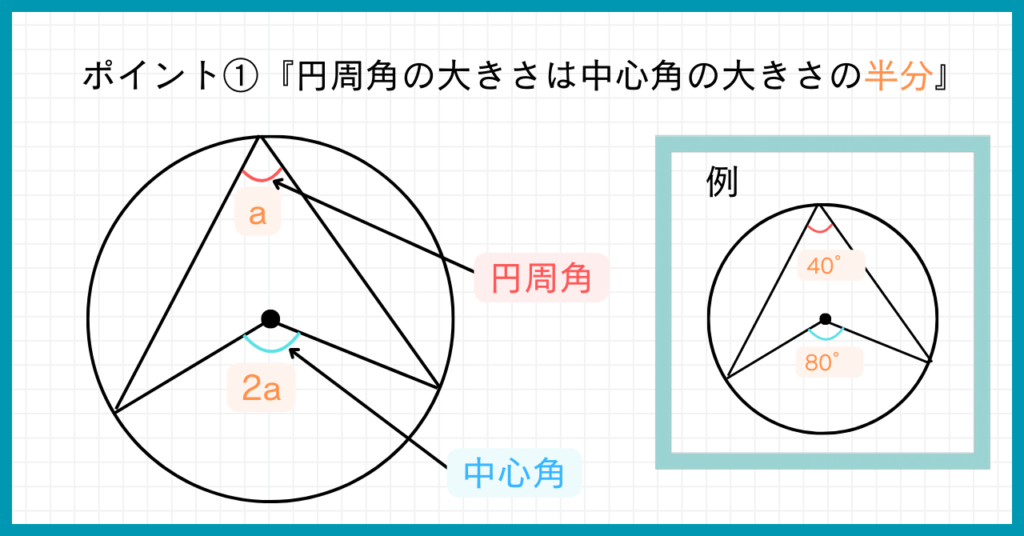
　まずは基本中の基本。円周角の大きさは、中心角の半分であることです。

　受験勉強をしている人にとっては当たり前のことかもしれません。

　しかし試験本番では以外と頭から抜けてしまうもの。今一度、確認しましょう。

②直径に対する円周角は90°

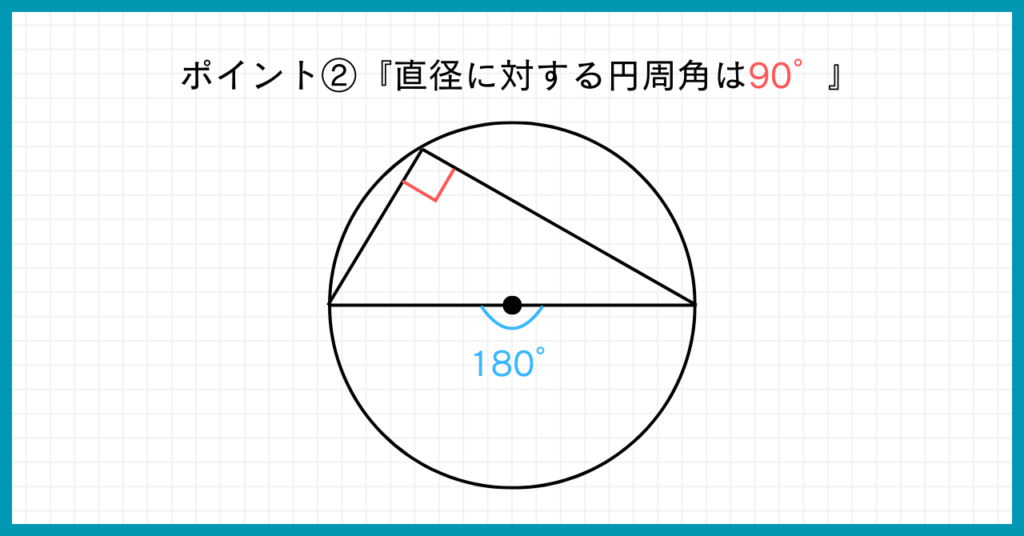
　直径に対する円周角は90°であることも、基本中の基本です。

　しかし問題に出てくる図には、上の画像のように『直角マーク』がない場合があるので、その時に『直径に対する円周角だ！』と気づかないことがあります。

　直角マークがなくても、直径に対する円周角は90°です。忘れないようにしましょう。

③円の半径の長さは等しい

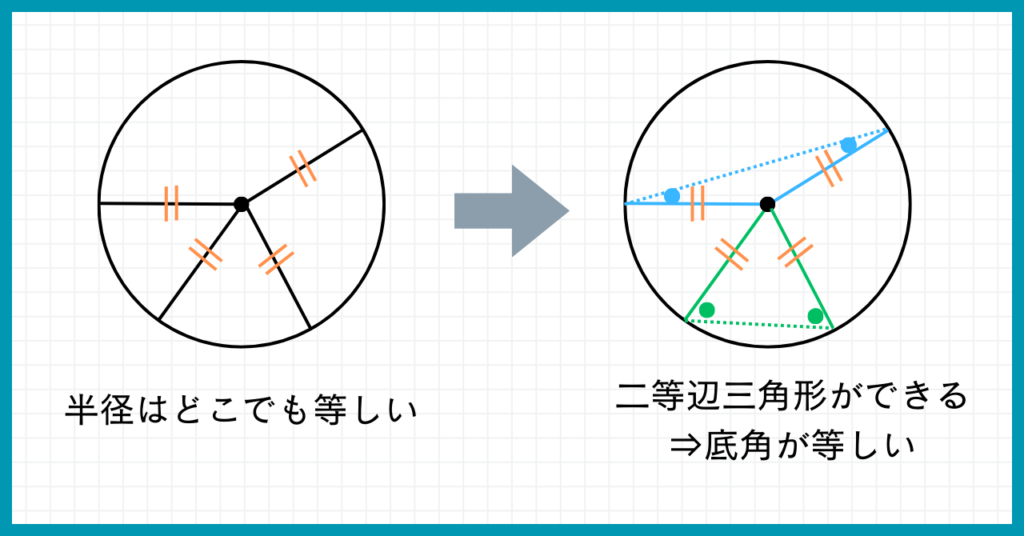
　円の半径は、どこをとっても長さが等しいことを抑えましょう。

　上の図のように補助線を引くと、二等辺三角形ができます。

　二等辺三角形といえば、底角が等しいですよね。

　底角が等しいことを利用して、円周角の問題を解くことがあります。

④中心角や円周角の大きさは、弧の長さに比例

　弧の長さと中心角・円周角との関係は知っていますか？

　中心角や円周角の大きさは、弧の長さに比例します。

　例えば弧の長さが2倍になれば、中心角や円周角の大きさが2倍になります。

　また、弧ABの長さと弧BCの長さの比が2:3であれば、弧ABに対する中心角や円周角の大きさと弧BCに対するそれの比も2:3になります。

⑤三角形の内角と外角の関係

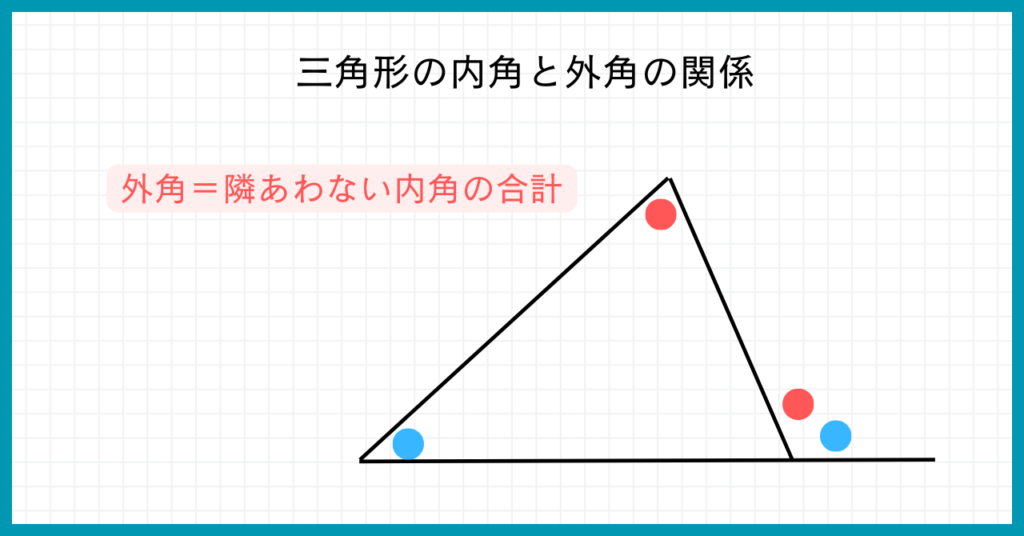
円周角のポイントなのに、三角形の話？

　円周角の問題でも、三角形の内角と外角の関係を用いることがあります。

　どうしても問題を解けない！　という時は、三角形の内角と外角の関係で解けることがありますよ。

　しかし、三角形の内角と外角の関係を使うかもしれないと意識していないと気づけないので、ここで確認しておきました。

【番外編】対頂角・錯角・同位角

　最後に、対頂角・錯角・同位角について確認しましょう。

　円周角に限らず、図形の問題であれば対頂角・錯角・同位角を用いることがあります。

　しかし三角形の内角と外角の関係と同様、対頂角・錯角・同位角を意識していないと気づけないので、基本だからと馬鹿にせず、しっかり確認しましょう。

まとめ～ポイントを駆使して円周角を求めよう

　都立高校入試では数学の大問1を全問正解することが重要です。

　しかし、大問1だからといって簡単に正解できるわけではありません。

　特に円周角の問題は、この記事で挙げたポイントを押さえていないと、そもそも解き方がわからないくなってしまいます。

　この記事を読んだあとは、教科書の節末問題や章末問題といった標準～応用問題に取り組みましょう。