【くもわは要らない】割合の公式を覚えなくても解けるようになる！割合の意味を解説

　割合の問題を難しく感じるのは、決してあなただけではありません。

　割合の問題は公式を暗記してしまえば解けるようになると考えている人が多いかもしれませんが、それだけで解けるようになるなら割合が苦手な人はほとんどいなくなるでしょう。

　では、なぜ割合の問題を解けないのか。それは割合の意味を理解せずに、公式の丸暗記に頼っているからです。

　比べられる数と元にする数の違いはわかりますか？　そもそも割合とはなんですか？

　この記事では割合の解き方を、割合の具体例を用いながら解説します。この記事の内容を理解すれば、『くもわ』の公式がなくても割合の問題を解けるようになりますよ。

割合を求めるのに『くもわ』は要らない

　本来、割合を求めるのに公式は要りません。

　例えば以下のような問題で、公式を意識して解くことはないでしょう。

　『30個のアメを6人で分けるとき、1人分は何個になるでしょう』

　割合だって、割合の意味さえ分かっていれば同じように公式を意識しなくても問題を解けます。しょせん割合の問題もただの『割り算』なのです。

　この後で、割合の公式を使わなくても問題を解けるよう、割合の意味から解説します。

　割合の問題を解くとき、多くの人は公式に当てはめて解こうとします。

　確かに公式を暗記していればすぐに計算できて便利ではあります。しかし割合が苦手な人は、この公式を使いこなせないのです。

　特に『くもわ』の公式を使って問題を解く人が多いですよね。とても便利な公式ではありますが、問題文中の何が『比べられる数』で何が『元にする数』なのか、完璧に区別できますか？

　この後の解説では、『比べられる数』と『元にする数』の意味もわかるので公式の当てはめで悩むことがなくなりますよ。

割合の意味を理解して公式を覚えなくても解けるようになろう

　ここからは『割合』『元にする数』『比べられる数』の意味を解説します。

　また、割合の問題が公式を使わなくても解けるよう具体例を用いながら解説します。

　ここを読めば、割合の文章題がただの割り算の問題になりますよ。

『割合』『元にする数』『比べられる数』を一言で言うと？

　そもそも『割合』『元にする数』『比べられる数』をそれぞれ説明できますか？

　割合が苦手な原因として、これらの意味をよくわかっていないことがあるので、ここで確認しておきましょう。

　例えば『40人のクラスのうち10人が身長160㎝以上のとき、このクラスには身長160㎝以上の人が25％いる』ならば、まず割合は『25％』ですよね。

　問題はどちらが『元にする数』でどちらが『比べられる数』か、です。

　元にする数は『割合を求めたい全体の数』なのでこの場合は『クラス全体の数』ですよね。よって元にする数は『40』です。

　比べられる数は『割合を求めたい数』です。この場合は『このクラスには身長160㎝以上の人が25％いる』ということで、身長160㎝以上の人の割合を求めたので比べられる数は身長160㎝以上の人の数、つまり『10』です。

割合の求め方を具体例で解説

　ここからは具体的に、割合の求め方を解説します。

　ここを読めば『割合』『元にする数』『比べられる数』が具体例で分かり、どのように計算すれば割合を求められるのかが分かります。

　そうすることで割合はあなたにとって公式を用いなければ解けない問題ではなくなるため、それがただの割り算の問題になりますよ。

1年生は、国語が好きな人は30人。

2年生は28人だから、1年生の方が多い！

でも1年生は全部で100人なのに、2年生は全部で70人。

全体の数が多ければ、その中で国語が好きな人が多くなるのは当然じゃない？

じゃあ、どうやって国語が好きな人の数を比べればいいの？

　全体の数が違うならば、単純に国語が好きな人の数を比べて、どちらの学年のほうが国語が好きな人が多いかを答えられません。

　そんなときに使うのが『割合』です。

　1年生と2年生それぞれの中で、どちらの方が国語が好きな人の割合が高いかを比べます。

　では、その『割合』をどうやって計算して出すか。

　一人当たりの『国語が好きな気持ち』はどれくらいか？を計算で出します。

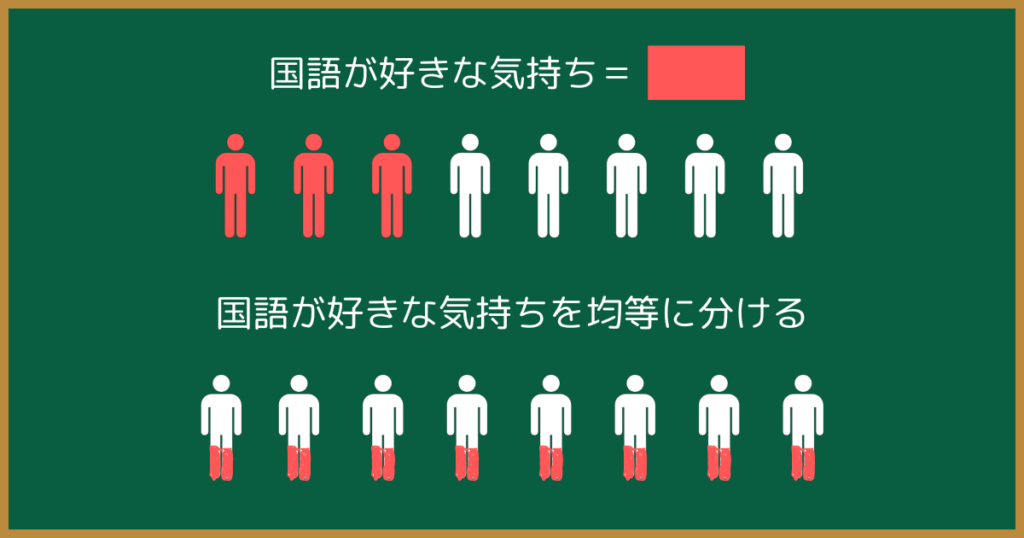
　このように1年生と2年生それぞれで、全員に国語が好きな気持ちを均等に分けたとき、一人当たりにある『国語が好きな気持ち』が多い方が割合が高いということになります。

　では、一人当たりにある『国語が好きな気持ち』を調べるにはどんな計算をすれば良いでしょうか。

　均等に分けるといえば割り算ですよね。

　『(国語が好きな人の数)÷(学年全体の数)』で、一人当たりの国語が好きな気持ちを分けることができます。

　では、1年生と2年生それぞれで、一人当たりの国語が好きな気持ち＝国語が好きな人の割合を求めていきましょう。

　1年生の国語が好きな人の割合は、

　$30÷100＝0.3$

　つまり$0.3×100＝30％$

　2年生の国語が好きな人の割合は、

　$28÷70＝0.4$

　つまり$0.4×100＝40％$

　よって、国語が好きな人の割合は2年生の方が高いので、2年生の方が国語が好きな人が多いと言えます。

割合から百分率の変換方法は以下の記事で解説しています。

　『(国語が好きな人の数)÷(学年全体の数)』で、一人当たりの国語が好きな気持ち＝国語が好きな人の割合を求めましたね。

　この『国語が好きな人の数』が『比べられる数』で、『学年全体の数』が『元にする数』です。

　比べられる数と元にする数をそれぞれ一言で言うと、『比べられる数＝割合を求めたい数』『元にする数＝割合を求めたい集団全体の数』だと説明しました。

　したがって、この問いで言うと割合を求めたかったのは『国語が好きな人』だったので『国語が好きな人の数』が『比べられる数』、その集団全体の数は1年生全員または2年生全員の数だったので『学年全体の数』が『元にする数』であるというわけです。

まとめ

　割合の求め方についてまとめます。

　割合の意味さえわかれば、『くもわ』の公式に頼らなくても式を立て問題を解けるようになります。

　また、比べられる数や元にする数を求める問いでは、比べられる数や元にする数を□や$x$でおけば解くことができます。

　計算を便利にするために公式があるのに、その公式の使い方でつまづいてしまっては元も子もありません。

　本質的な意味をしっかり理解していきましょう。