【丸暗記なし!】余弦定理の公式の覚え方を三平方の定理から理解する
余弦定理の公式って、文字がいっぱいあって覚えにくいですよね。
おまけにcosAとか、なんだか嫌になっちゃいます。

余弦定理の公式は3つもあるから覚えるのが大変!
余弦定理にはa2,b2,c2から始まる3種類の公式ががあります。
でも、あなたが覚えなければならないのは1種類です!
3つの公式は全て本質は同じなので、それぞれの公式を丸暗記する必要はないのです。
この記事を読めば簡単に余弦定理の本質を理解し、公式を覚えることができるようになります。
この記事の流れ
余弦定理の本質を理解するためにはまず三平方の定理を理解している必要があります。
なので次のような流れで解説します。
好きなところから読んでくださいね!
この記事がオススメの人
- 余弦定理の公式を覚えられない人
- 余弦定理の公式を難しいと思ってる人
- 余弦定理の公式の本質を知りたい人
まずあなたの誤解を解かなくてはなりません。
余弦定理は高校で初めて出会った未知の公式ではないのです!
だから、難しい話ではまったくないのですよ。

余弦定理なんて中学まででは出てこなかったぞ?
余弦定理は、中学で『三平方の定理』という名前で出てきました。
実は、三平方の定理は余弦定理から導くことができるのです。これについては後で解説しますね(⇒余弦定理の公式から三平方の定理を導ける)
さて、三平方の定理は覚えていますか?
三平方の定理を理解していれば、余弦定理も本質から簡単に理解できます。

三平方の定理ってなんだっけ?
三平方の定理の公式や意味を忘れてしまった人のために、以下で三平方の定理について解説します。
三平方の定理なんか余裕! という人は読み飛ばしてOKです。⇒三平方の定理から余弦定理を考える
三平方の定理の本質を解説
まずは三平方の定理の公式を確認しましょう。
つまり三平方の定理とは、斜辺の二乗=その他の辺をそれぞれ二乗した和ということです。
この三平方の定理の意味をよく覚えておいてください。
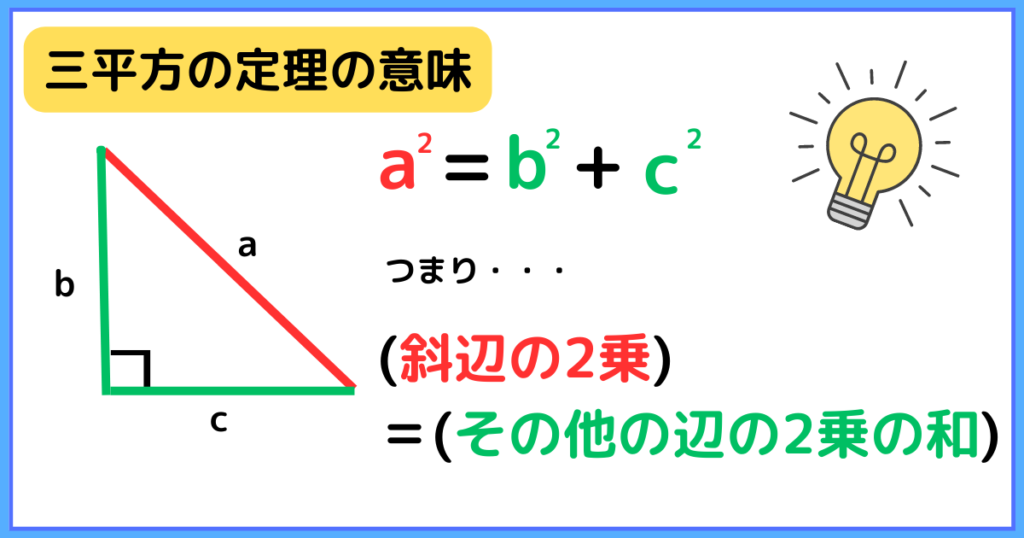
さらに言い換えると、三平方の定理は直角と直角に向かい合う辺(斜辺)に注目した公式です。
これが三平方の定理の本質であり、後に学ぶ余弦定理に繋がるのです。

三平方の定理から余弦定理の本質を考える
三平方の定理の公式を理解したところで、余弦定理の本質に迫ります。
余弦定理の公式は1つ覚えればいい
まずは余弦定理の公式を確認しましょう。

余弦定理の公式って3つあったよね?
ここに書いたのはa2から始まる公式のみです。
他にもb2やc2から始まる式がありますが、覚えるのは1つだけでOKです!
なぜなら、3つの公式は全て本質が一緒だからです。
余弦定理の公式を本質から覚える
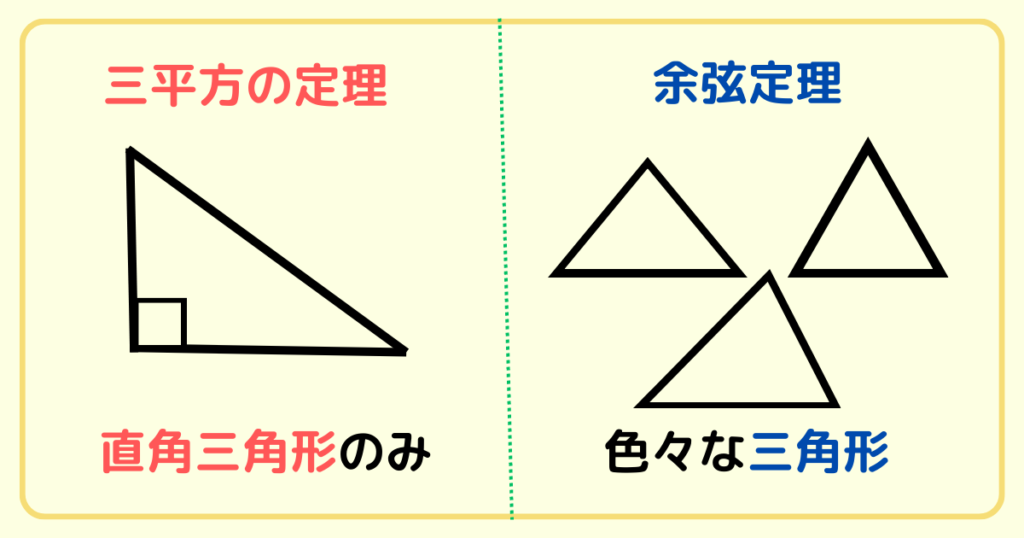
三平方の定理は、直角三角形のみで成り立ちますよね。
対して余弦定理は、どんな三角形でも成り立つのです。
さて、先ほど示した三平方の定理の本質は覚えていますか?

三平方の定理の本質は、直角と直角に対する辺(斜辺)に注目した定理であること!
余弦定理の本質は三平方の定理と同じです。
三平方の定理の本質を元に、余弦定理の本質は次の様に言うことができます。
三平方の定理は直角三角形のみに当てはまりましたが、余弦定理は色々な三角形に当てはまります。
だから、直角ではなく『ある角』と『ある角に対する辺』としました。
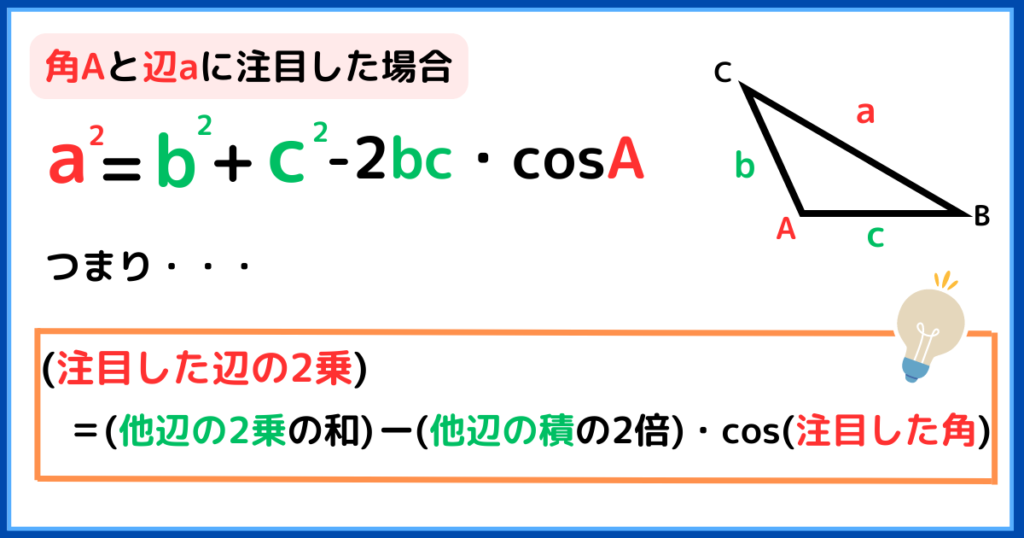
余弦定理の公式を文字や記号の羅列と考えていると暗記するのに苦労します。
しかしこのように本質を理解するとすぐに覚えられますし、忘れにくくなりますよ。
余弦定理の公式から三平方の定理を導ける
三平方の定理と余弦定理の本質は同じであることを繰り返しお伝えしてきました。
なぜそれらの本質は同じなのでしょうか。
そもそも余弦定理も三平方の定理も同じ物なのですよ。
三平方の定理は、余弦定理から導けるのです。

直角と直角に対する辺(斜辺)に注目するということは、公式にcos90°を当てはめることになります。
cos90°=0ですよね。

この様に、三平方の定理は余弦定理から導くことができるのです。
まとめ
余弦定理の本質は、『ある角と、ある角に対する辺に注目した定理であること』でした。
あなたが難しいと思っていた余弦定理。
実は中学で習った三平方の定理の本質と繋がっていましたね。
一見すると難解な公式も、この様に本質をつかめば簡単に理解できます。
丸暗記ではなく、本質はなんなのか?を考えるようにしましょう。

コメントを残す