【高校数学Ⅰ】ルートの中が文字式の時のルートの外し方を解説

高校の数学Ⅰではルートの中が文字式になることがあります。
ルートの中が文字式になると、どうやってルートを外せばいいか迷ってしまいますよね。
数学Ⅰは中学の延長です。難易度が上がったとしても、中学内容をしっかり理解していれば高校の数学もマスターできますよ。
ルートの中身が数字でも文字でも、ルートの外し方は同じです!
ルートの中は必ず正の数になるので、ルートを外したときに正の数になるよう、絶対値を付けて処理すればいいのです。

ルートの中は必ず正の数?
絶対値を付ける?
どういうこと!?
ルートの基本事項がピンとこない人のために、この記事ではまずルートの中身が正の数、負の数、文字式で共通するルートの外し方を、基本から解説します。
その後でルートの中が文字式の時のルートの外し方を詳しく解説し、最後にルートの中が文字式の時の例題を紹介します。
高校2年生の数学(数学Ⅱ)ではルートの中がマイナスになる『虚数』を勉強しますが、高1の皆さんはまだ考えなくて大丈夫です。
ルートの外し方『基本』を解説【正の数、負の数、文字式共通】
ルートの中が文字式でも、正の数でも負の数でも共通するルートの外し方を解説します。
以下で詳しく解説します。
【大前提】ルートの中は必ず正の数
まず大前提として、ルートの中は必ず正の数であることを押さえましょう。
そもそもルートとは、2乗したらルートの中の数になるという意味です。
例えば$\sqrt{3}$とは2乗したら3になる数という意味です。
2乗して負の数になるなんてありえないですよね。
よって、ルートの中の数は正の数でないとおかしいのです。
ルートの基本について詳しく知りたい人は、以下の記事も読んでくださいね。
ルートを外すときは絶対値記号をつける
ルートの中は必ず正の数であると解説しました。
つまり、ルートを外したら必ず正の数がでてこないといけません。
では、どうやってルートを外せば良いか。
ルートの中が正の数でも負の数でも、文字式のときも、ルートを外すときは中の数に絶対値記号をつければよいのです。
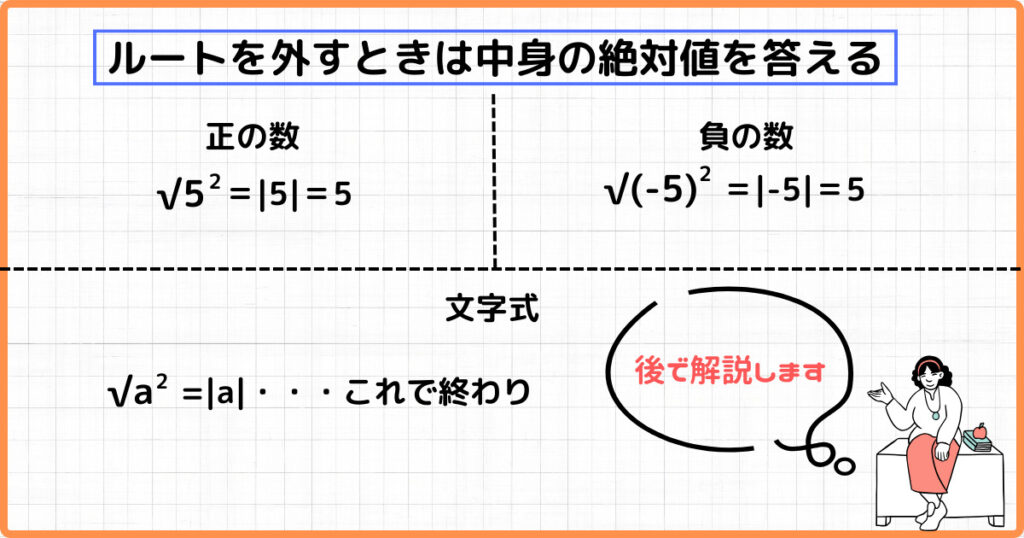
中学までで習った内容を踏まえて、次の問題を解いてみましょう。
$\sqrt{ (-3)^2 }$からルートを外してみよう。
$\sqrt{ (-3)^2 }=|-3|=-(-3)=3$
ルートを外すときは絶対値記号をつけると意識しましょう。
これが意識できていないと、ルートの中身が文字になったときに混乱してしまいます。

$\sqrt{ (-3)^2 }=√9=3$
じゃダメなの?
それでも正解です。
多くの人はこの方法を中学で勉強したんじゃないでしょうか?
でも、このやり方で慣れてしまうと、高校数学でルートの中身が文字の時にルートの外し方を理解するのが難しくなってしまうのです。
だから、ルートを外すときは絶対値記号をつけると覚えてください。
ピンと来ていない人は、まずこちらの記事を読んでから戻ってきてください。
ルートの中身が文字の時のルートの外し方
ここからはルートの中身が文字式の時の、ルートの外し方を解説します。
ルートの中身が文字式の時は、その文字式の正負がわかっているかわかっていないかで、ルートの外し方が変ります。
まずはルートの中身の文字式の正負がわかっていない場合を解説し、そのあとで正負がわかっている場合を解説します。
①文字式の正負がわかっていない場合
さて、ここで問題です。
$\sqrt{ A^2 }$からルートを外すとどうなるでしょうか?

$\sqrt{ A^2 }=A$ じゃないの?
実はこれ、間違いです。
正解は、$\color{red}{\sqrt{ A^2 }=|A|}$ です。

なんで絶対値記号がついたままなの?
みなさんは、このAが正の数であると決めつけていませんか?
平方根の単元に限らず、特に条件の書いていない文字はあらゆる可能性を考えなくてはいけません。
この場合は、Aが負の数の可能性です。
Aの正負がわかっていないので、この問いでは絶対値記号をつけたままで止めておきます。
②文字式の正負がわかっている場合
正負がわかっている場合は、以下のように絶対値記号を外します。

A<0はなんで絶対値を外した後にマイナスが付くの?
ルートの中身は必ず正の数と決まっています。
$\sqrt{ A^2 }$のAが負の数だった場合、ルートを外したあとはAの絶対値(マイナスを取った数)を答えなくてはいけません。

この時と同じように、絶対値記号の中身が負の数(A<0)の時はAにマイナスをつけるのです。
中学校で習ったままに、
$\sqrt{ (-A)^2 }=\sqrt{A^2 }=A$
のように考えてしまった人は要注意! 必ず絶対値での考え方を身につけておきましょう。
【例題】ルートの中身が文字式の時の外し方
ルートの中が文字の時のルートの外し方を、例題を解きながら理解しましょう。
例題
$\sqrt{ a^2b^4 }$のルートを外そう。
ただし、$a<0、b>0$とする。

文字が2個あるし、bは4乗?
どうすればいいんだ?
ルートを外すためには、ルートの中が$A^2$の形にならなければいけません。
まず初めに、ルートの中身が2乗の形になるように変形しましょう。
すると、ルートを外すことができるようになります。

ルートを外した後は忘れずに絶対値をつけよう!


これで解答は終わりなの?
これで終わりではありません。
この問いでは$a<0、b>0$という条件があるので絶対値を外すことができます。

絶対値を外すためには、正の数が負の数かを判定しなきゃいけないね

以上より、答えは-ab2です!
まとめ~ルートを外すときは中身の絶対値を答える!
ルートの中が整数でも文字式でも、ルートの外し方は同じです。
ルートを外すときはルートの中の数の絶対値を答える。
この本質をしっかり覚えてくださいね。

コメントを残す